§ 8.2.4. Применение простого дискриминантного критерия

Простой дискриминантный критерий (см. § 4. 3) позволяет найти пространство из минимального числа признаков, сохраняющее среднюю меру различий между образами - среднеквадратичное расстояние между реализациями различных образов - не менее заданной величины.

Свойством простого дискриминантного критерия является то, что в найденной системе признаков внутриклассовая дисперсия по всем направлениям одинакова, а сумма дисперсий центров тяжести, которая пропорциональна среднеквадратичному расстоянию между реализациями различных образов, распределена по найденным осям координат наиболее неравномерно. Это видно на рис. 8.5, на котором показаны зависимости дисперсии центров тяжести от номера признака, найденного по простому дискриминантному критерию, и от номера параметра исходного описания. На рисунке дисперсия центров тяжести начиная с 11-го признака, найденного по простому дискриминантному критерию, равна нулю, так как 11 точек, представляющих 11 центров тяжести, всегда лежат не более чем в 10-мерном пространстве.

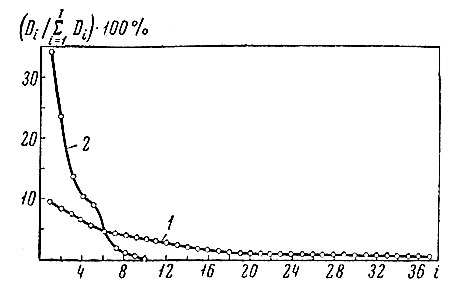
8.5. Зависимость дисперсии центров тяжести от номера параметра (7) исходного описания и (2) признака, найденного по простому дискриминантному критерию

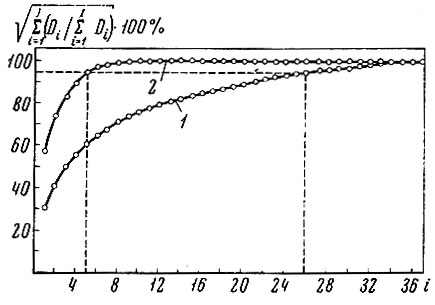
8.0. Зависимость среднеквадратичного расстояния между центрами тяжести образов в процентах от числа используемых параметров (7) исходного описания и (2) признаков, найденных по простому дискриминантному критерию

Наибольшая неравномерность распределения дисперсий центров тяжести по признакам, найденным с помощью простого дискриминантного критерия, позволяет при отбрасывании (I-J) последних признаков (соответствующих наименьшим дисперсиям центров тяжести) получить минимальную среднеквадратичную ошибку для векторов, соединяющих центры тяжести образов. И наоборот при заданной средне-квадратической ошибке аппроксимации векторов, соединяющих центры тяжести образов, получить минимальное число признаков.

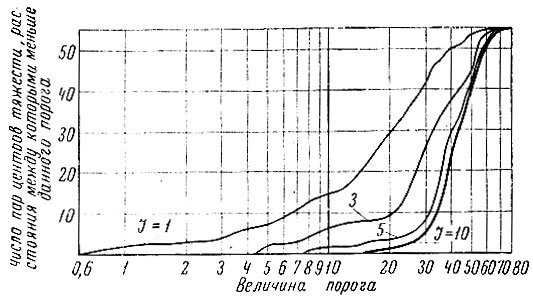
8.7. Гистограммы взаимных расстояний в мерке l₂ между центрами тяжести образов 1, 3, 5 и 10-мерном подпространствах, найденных по простому дискриминантному критерию

На рис. 8.6 изображены графики зависимости средне квадратичных расстояний между центрами тяжести образов от числа используемых параметров исходного описания признаков, найденных по

простому дискриминантному критерию. Из сравнения графиков следует, что для получения приближения векторов, соединяющих центры тяжести с 5%-ной среднеквадратичной ошибкой в пространстве простых дискриминантных признаков, требуется пять признаков. Такая же величена ошибки аппроксимации в пространстве исходного описания имеет место при использовании 26 исходных параметров.

Перейдем теперь к обсуждению недостатков простого дискриминантного критерия.

При нахождении признаков "о простому дискриминантному критерию может быть обеспечена достаточно малая величина среднеквадратичной о аппроксимации. Однако известно, что при средне-квадртичной аппроксимации векторов направления координатных осей разложения зависят не только от ориентации векторов в исходном пространстве, но и от квадра их нормы. Поэтому признаки, находимые по простому дискриминантному критерию, в первую очередь будут учитывать различия между "далекими" образами.

На рис. 8.7 изображены зависимости числа пар образов, расстояние (в метрике l₂) между центрами тяжести которых меньше пороговой величины, от величины этого порога (гистограммы взаимных расстояний между центрами тяжести образов). Гистограммы получены для подпространств, образованных 1, 3, 5 и 10 признаками, находимыми по простому дискриминантному критерию. Из них видно, что в пространстве простых дискриминантных признаков прежде всего хорошее приближение действительно соответствует наиболее далеким парам образов.

Заметим, что при выполнении любых линейных преобразований над пространством исходного описания сравнение абсолютных величин расстояний в исходном пространстве X и в сокращенном пространстве признаков

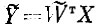
требует введения некоторых ограничений, чтобы исключить возможность получения тривиального решения путем простого изменения масштаба исходных параметров. Во всех экспериментах этой главы при нахождении линейных преобразований W̃^T требовалось сохранение постоянства среднеквадратичного расстояния между центрами тяжести образов в пространстве

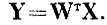
В таблице 8.3 представлены взаимные расстояния между центрами тяжести образов в метрике l₂ в пространстве с нормированной внутриклассовой дисперсией

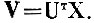
В таблице 8.4 представлены взаимные расстояния между центрами тяжести образов в пятимерном пространстве простых дискриминантных признаков. Из таблиц видно, что длины проекций векторов, соединяющих наиболее "близкие" пары центров тяжести (см. пары "два" и "ноль", "четыре" и "читаю", "один" и "три"), намного уменьшились.

В то же время относительное уменьшение расстояний между проекциями далеких пар центров тяжести (см. пары "пять" и "семь", "шесть" и "читаю", "пять" и "читаю", "семь" и "восемь") очень невелико.

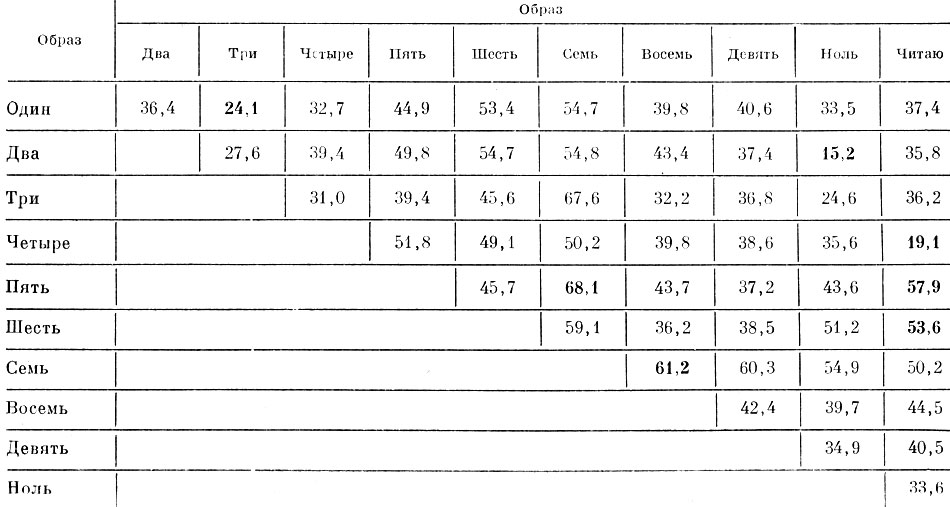
Таблица 8.3. Расстояния между центрами тяжести образов в метрике l₂ в пространстве, где нормирована внутриклассовая дисперсия

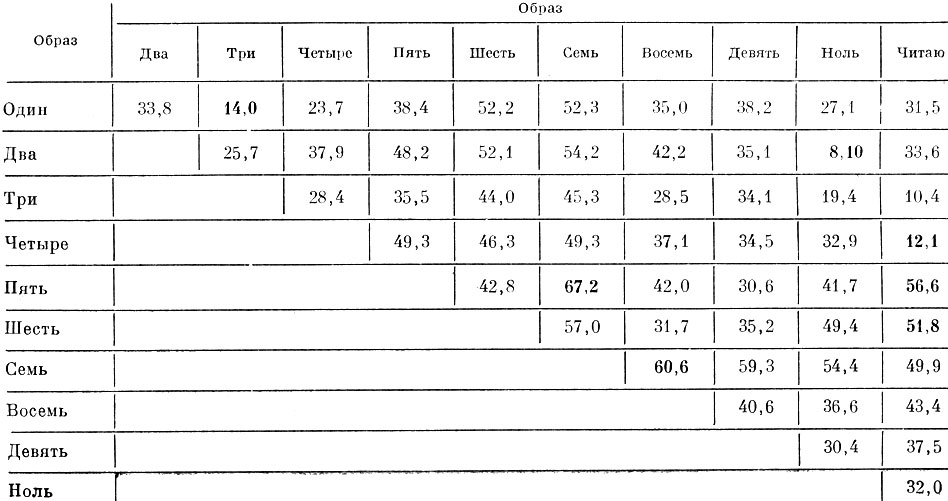
Таблица 8.4. Расстояния между центрами тяжести образов в метрике 12 для 5-мерного подпространства признаков, найденных по простому дискриминантному критерию