§ 8.2.9. Сравнение экспериментальных результатов создания признаков по различным критериям

Признаки создаются для построения решающего правила. Различным решающим правилам адекватны свои системы признаков. Поэтому сравним отдельно критерии создания признаков, адекватные решающему правилу в метрике l₂ и в метрике с.

Начнем с признаков, адекватных решающему правилу в метрике l₂. Сравним между собой количество признаков, обеспечивающих разделимость в системах, образованных по критериям: взвешенному дискриминантному (§ 4.4),

простому дискриминантному (§ 4.3) и аппроксимационному (§ 4.2).

В пространстве признаков, найденных по взвешенному дискриминантному критерию, разделимость обеспечивалась только четырьмя признаками. При этом минимальное расстояние (в метрике l₂) между центрами тяжести уменьшилось (по сравнению с исходным пространством) всего на 2,6%.

Тот же результат - уменьшение расстояний между наиболее близкой парой образов на 2,6% - потребовал пространство из девяти признаков, найденных по простому дискриминантному критерию, или пространство из 17 признаков, найденных по аппроксимационному критерию.

Таким образом, взвешенный дискриминантный критерий обладает существенными преимуществами (с точки зрения сохранения разделимости образов) перед простым дискриминантным и аппроксимационным критериями.

Перейдем теперь к критериям, адекватным решающему правилу в метрике с.

Блок опознающего автомата, принимающий решение в метрике с, значительно проще этого же блока, принимающего решение в метрике l₂. Но поскольку в метрике с должна иметь место одномерная покоординатная разделимость, требования к признакам здесь более жесткие, так как они относятся к каждому признаку в отдельности.

Поэтому для одной и той же задачи число признаков, обеспечивающих разделимость в метрике с, может оказаться большим, чем для метрики l₂. В приведенном эксперименте для обеспечения разделимости 6-ти образов потребовалось 6 признаков для метрики с и 4 признака для метрики l₂.

Общим для рассмотренных в § 4.7, 4.8 одномерных критериев является возможность находить разделяющие признаки, обеспечивающие расстояние в метрике с между реализациями различных образов не менее заданного порога

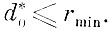
Одномерный детерминистский критерий целесообразно применять в тех случаях, когда величина порога d*₀ близка но величине к минимальному расстоянию Опт между выборками в пространстве V, измеренному в метрике l₂. Если же порог d*₀ можно выбрать существенно меньшим величины r_min, то предпочтительнее взвешенный одномерный дискриминантный критерий, который за счет усреднения позволяет сократить число признаков.

Эксперименты, проведенные после сдачи книги в набор, показали, что дополнительное применение одномерных нелинейных преобразований позволило существенно улучшить разделяющие свойства системы линейных признаков. Заметим, что одномерные кусочно-линейные преобразования легко реализуются при помощи стандартных нелинейных блоков аналоговых вычислительных машин.

При влечении сохранить денежные средства не во вред первоклассности совокупления, заказывайте самостоятельных индивидуалок на вебстраничках секс сайта https://prostitutkiekaterinburga777.win. Тут подобраны верные анкетки женщин разных возрастов.