§ 8.4.2. Получение признаков с использованием в качестве исходного описания непрерывных сигналов датчиков

Пусть на автомат подаются два напряжения Р (t) и S (t). На плоскости Р (S) будет иметь место динамограмма, изображенная на рис. 8.17.

Четыре характерных точки на динамограмме представляют собой минимум сигнала хода S (t) (точка 1), максимум сигнала усилий Р (t) (точка 2), максимум сигнала хода S (t) (точка 3), минимум сигнала усилий Р (t) (точка 4).

На рис. 8.17 значения усилия Р, хода S в указанных точках обозначены соответственно через

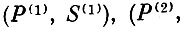
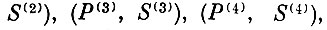
а соответствующие им моменты времени обозначены через

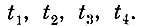
Разобьем участок усилий

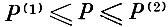
на I/2 интервалов, каждый из которых обозначим Δ₁P_i. Аналогично поступим с участком

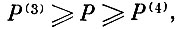
и интервалы на этом участке обозначим Δ₂Р_i.

Введем понятия относительного усилия χ_i и относительного приращения усилия Δχ_i. Тогда

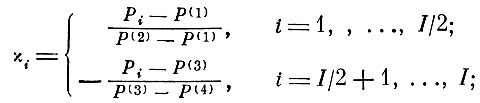(8.4.1)

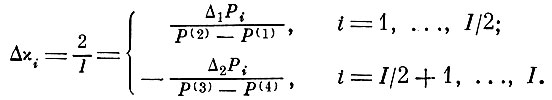(8.4.2)

Из формулы (8. 4. 2) видно, что относительное приращение усилия Δχ_i представляет собой постоянную величину, обратно пропорциональную общему числу интервалов I.

Введем, кроме того, понятие относительного перемещения х. Значения х_i в точках χ=χ_i имеют вид

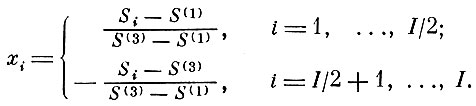(8.4.3)

Совокупность значений x=χ_i представляет собой выбранное нами исходное описание X, на основе которого были созданы два признака y₁, y₂, по которым затем принималось решение (см. § 8.3).

Если обозначить оптимальную матрицу перехода от пространства параметров исходного описания X в пространство признаков Y через W^T, то значения двух признаков, которые, как это следует из эксперимента, необходимы и достаточны для диагностирования, можно записать в виде

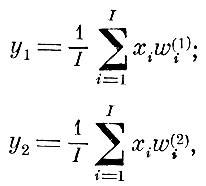(8.4.4)

где w⁽¹⁾_i представляет собой I-й элемент первой строки матрицы W̃^T, а w⁽²⁾_i-i-и элемент второй строки.

В значение признаков (ф-ла 8. 4. 4) входит число элементов, равное I. Заменим величину I связанной с ней величиной относительного приращения усилия Δχ_i (формула 8.4.2). Тогда

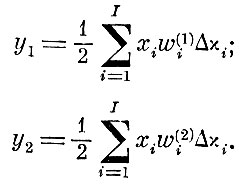(8.4.5)

Величина Δχ_i. зависит от числа интервалов I. При большом числе интервалов эта величина достаточно мала. Можно перейти к пределу, устремляя I к бесконечности.

При этом Δχ_i. будет стремиться к дифференциалу dχ, а сумма заменится интегралом. Значения признаков будут стремиться к значениям y*₁ и y*₂, несколько отличающимся из-за замены суммы интегралом:

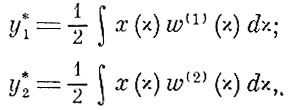(8.4.6)

где функции

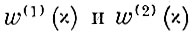
получены при помощи интерполирования по дискретным значениям

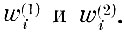
Интегрирование производится при изменении

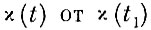
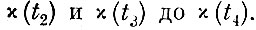
Вводим новые функции

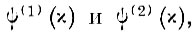
получаемые как интегралы весовых функций:

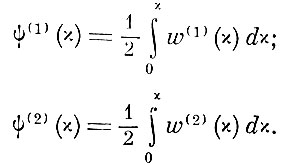(8.4.7)

При известных значениях

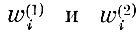
в дискретных точках функции

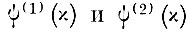
легко вычисляются.

Подставляя новые функции (формула 8. 4. 7) в уравнения для признаков (8. 4. 6), умножая и деля на dt, а также учитывая, что каждая из рассмотренных величин является в конечном счете функцией времени, получаем

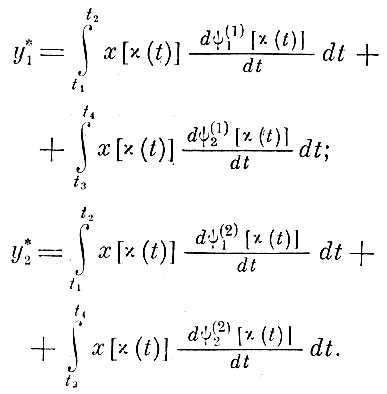(8.4.8)

Для аналогового нахождения признаков необходимо перейти к исходным величинам Р (t) и S (t). Это нетрудно сделать, подставляя в формулу (8. 4. 8) значения исходных параметров по формулам (8. 4. 1), (8. 4. 2), (8. 4. 3):

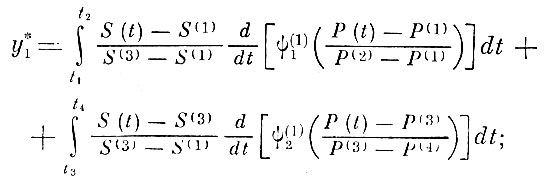(8.4.9)

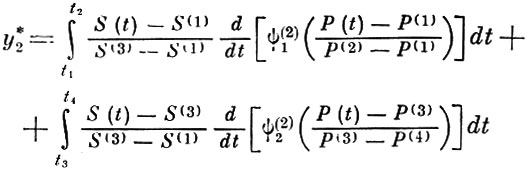(8.4.9)

Формула (8. 4. 9) для признаков y*₁, y*₂ является исходной для создания проекта аналогового автомата.

Проектирование автомата можно упростить, несколько преобразовав исходную формулу (8. 4. 9)..

Обозначим

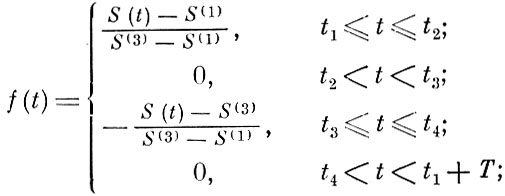(8.4.10)

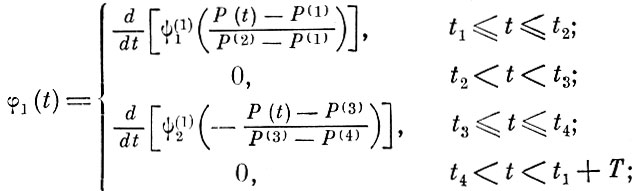(8.4.11)

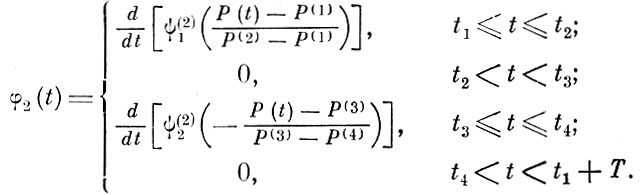(8.4.12)

Подставляя значения f(t), φ₁(t) и φ₂(t) по формулам (8. 4. 10), (8. 4. 11) и (8. 4. 12) в (8. 4. 9), получаем окончательное выражение для признаков y*₁, y*₂, удобное для проектирования автомата:

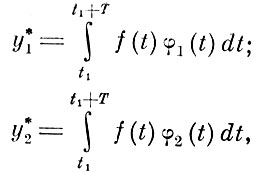(8.4.13)

где T - полный период работы насоса.