§ 0.3. Формальные нейроны

Формальный нейрон^* в смысле Мак-Каллока [13] описывается следующим образом.

^* (Для краткости слова "формальный нейрон" будем заменять словом "нейрон".)

1. Нейрон имеет конечное число входов а₁,...,а_n, по которым воспринимаются сигналы, и один выход, по которому сигналы выдаются (при n = 3 см, например, рис. 0.1).

2. Каждый из входов и выход могут принимать только одно из двух состояний: возбужденное (ставим в соответствие с единицей) или невозбужденное (ставим в соответствие с нулем).

3. В нейроне различают тело (сому) и волокна. Волокна начинаются на входах; каждое волокно может активироваться только тогда, когда возбужден вход, которому оно принадлежит.

Типы волокон:

а) возбуждающие; каждое возбуждающее волокно оканчивается на теле нейрона и в активированном состоянии вводит положительную единицу возбуждения (+1);

б) тормозящие; каждое тормозящее волокно оканчивается на теле нейрона и вводит в активированном состоянии отрицательную единицу возбуждения или, иначе, тормозящую единицу (-1);

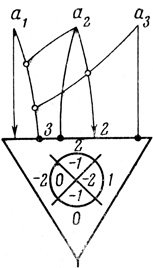
Рис. 0.1

в) запрещающие; каждое запрещающее волокно при возбуждении входа, которому оно принадлежит, предотвращает прохождение сигнала по другому волокну, на котором оно оканчивается.

Волокна могут ветвиться, но не могут объединяться.

4. Одной из основных характеристик нейрона является порог Θ, выражающийся целым числом. Изменение порога во времени задается конечным набором различных целых чисел {Θ₁,..., Θ_k}, расположенных (для определенности) в порядке убывания. В каждый данный момент времени t порог Θ принимает определенное значение Θ^t_j из набора {Θ₁,...,Θ_k}.

5. Сигналы (возбуждения) могут проходить только в одном направлении: от входов к выходу (на рисунках сверху вниз). При переходе сигналов через синапс (место контакта волокна с телом нейрона) происходит задержка на единицу времени. Таким образом, предполагается квантование времени; единицу квантованного времени составляет синаптическая задержка.

6. Если суммарное воздействие, приходящее на нейрон от всех волокон, в момент времени t достигает порогового значения Θ^t_j (или превосходит его), то в момент времени (t + 1) происходит возбуждение выхода нейрона. При определении суммарного воздействия волокон на нейрон необходимо учесть только возбуждающие и тормозящие единицы, поступающие от активированных в момент времени t входов с учетом при- 0-1 О-z аз надлежащих этим входам запретов

Формальный нейрон считается заданным, если известны все его волокна по числу, типу и распределению по входам.

На рис. 0.2 показан пример нейрона в символах, предложенных в [13]. На рис. 0.1 тот же нейрон изображен в символах, принятых в настоящей работе. Тело нейрона (сома) изображается в виде треугольника, внутри которого могут помещаться диаграммы, описывающие функционирование нейрона (на рис. 0.1 - пороговая диаграмма нейрона; см. § 2.3). Возбуждающие волокна заканчиваются стрелкой, а тормозящие - точкой на горизонтальной стороне треугольника.

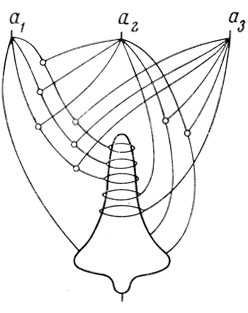
Рис. 0.2

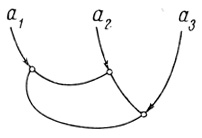
Рис.0.3

В настоящей работе в отличие, например, от [13, 16-18] допускается так называемый "запрет запрета": запрет запрещающего волокна.

Замкнутой цепью называем последовательность запрещающих волокон ξ₁,...,ξ_l(l > 1)" в которой волокно ξ_i оканчивается на волокне ξ_i+1, i = 1,..., l - 1 у а волокно ξ_l - на волокне ξ₁ (пример замкнутой цепи запрещающих волокон для 1=3 приведен на рис. 0.3)^*

Предполагаем, что запрещающие волокна не образуют замкнутых цепей.

^* (Для уточнения направления основного сигнала на запрещаемых ветвях некоторых рисунков поставлены стрелки, не касающиеся тела нейрона; стрелки же, касающиеся тела нейрона, как сказано выше, во всех случаях обозначают возбуждающие ветви.)

Пучок волокон, изображаемый в виде одного воликна с числом (весом), указывающим количество волокон в пучке, называется ветвью. Вес возбуждающих φ_ai и тормозящих ζ_ai ветвей записывается в виде числа без знака справа от ветви возле синапса; для всех φ_ai = ζ_ai = 1 вес ветви на рисунках не указывается. Запрещающие волокна (ветви) оканчиваются петельками, охватывающими запрещаемые волокна (ветви). На рис. 0.1 входу а₁ принадлежат одно возбуждающее волокно (или иначе - возбуждающая ветвь с весом 1) и три тормозящих (тормозящая ветвь с весом 3); входу а₂ принадлежат одно тормозящее волокно (тормозящая ветвь с весом 1), два возбуждающих (возбуждающая ветвь с весом 2) и три запрещающих волокна (запрещающая ветвь с весом 3), которые запрещают тормозящую ветвь с весом 3, принадлежащую входу входу а₃ принадлежат одно тормозящее волокно, две запрещающие ветви, идущие одна - на возбуждающую ветвь с весом 2, принадлежащую входу а₂, другая - на тормозящую ветвь с весом 3, принадлежащую входу а₁.

Обозначим количество волокон, принадлежащих входу а_i, возбуждающих- через φ_ai, тормозящих - ζ_ai запрещающих - ζ_ai суммарное число всех волокон нейрона по типам обозначим теми же буквами, но без индексов, общее число волокон, принадлежащих входу а_i - через W_ai, а общее число всех волокон нейрона - W. Кроме того, обозначим число ветвей: общее - через V, принадлежащих входу а_i - через V_ai, возбуждающих - Уф, тормозящих - V_ζ, запрещающих - V_ξ. Тогда показанный на рис. 0.1 и 0. 2 нейрон имеет:

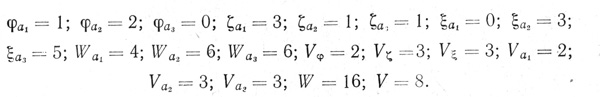
Формальный нейрон будем обозначать буквой А; для обозначения места нейрона в сети иногда будет использоваться обозначение A_r,i, где r - номер ранга (ряда) сети, а i - номер нейрона в данном ряду (считая слева направо); в ряде случаев, когда необходимо отметить все входы (переменные) нейрона, последний будем обозначать А(а₁,..., а_n) или A_r,i (a₁,..., а_n).

Из формальный нейронов можно строить сети, называемые нейронными.

В общем случае под нейронной сетью будем понимать совокупность конечного числа нейронов, выходы которых могут быть произвольно подсоединены ко входам некоторых нейронов.

Мак-Каллок рассматривал существенно более упорядоченные сети: первый ряд (ранг) сети содержит n нейронов (n - число входов каждого нейрона); выходы нейронов первого ранга являются входами нейронов второго ранга; последующие ранги строятся по этому же правилу; последний ранг состоит из одного выходного нейрона.

Для описания функционирования формальных нейронов и образуемых из них сетей используются символы и диаграммы Венна (описанные в главе 1 настоящей работы).

В функционировании нейронов и сетей нас будет интересовать выход прежде всего как функция входа, а также как функция входа и времени (особенно для нейронов и сетей с обратными связями).

Сделаем еще одно замечание, относящееся больше к терминологии, нежели к сути дела. В литературе пороговые элементы нередко называют нейронными. Между тем, на наш взгляд, между ними имеется принципиальное различие: в нейроне предусмотрена нестабильность порога и имеется третий из встречающихся в живом мозге тип волокон (запрещающие волокна), чего нет в пороговом элементе. Пороговый элемент представляет собой частный случай формального нейрона, у которого зафиксирован порог и отсутствуют запрещающие волокна. Естественно, что в связи с этими ограничениями функциональные возможности порогового элемента по сравнению с формальным нейроном снижены (см. § 5.1).

Для конкретности будем представлять себе формальные нейроны как некоторые физические объекты, которые не обязательно существуют в настоящее время, но которые принципиально могут быть созданы. Калбертсон [19] считает, что на настоящем этапе развития теории нейронных сетей нет необходимости требовать немедленного создания нейронов как отдельных деталей реальных машин; однако, по его мнению, нейроны могут служить одним из примеров универсальных атементов для конечных автоматов; если принять эти нейроны за основные логические элементы, то становится очень удобным описывать как схемы (например, ЭЦВМ), так и способы их функционирования. Это, разумеется, не исключает возможности появления в ближайшем будущем технических реализаций формальных нейронов на основе современной микроэлектроники (с использованием техники тонких пленок, твердых схем и т. п.).