§ 5.4. О возможностях синтеза некоторых устройств ЭЦВМ из надежных оптимальных нейронных сетей

Изложенные в настоящей работе принципы можно применить для синтеза ряда устройств дискретной электронной техники в терминах оптимальных формальных нейронов. Сделаем это на примерах, взятых из электронной цифровой вычислительной техники.

Наибольший интерес представляет синтезирование из формальных нейронов двоичного сумматора. Выполняя арифметическое сложение двух чисел, сумматор является основой арифметического узла электронной цифровой вычислительной машины. Все другие действия (умножение, деление, сравнение чисел и др.) в подавляющем большинстве современных ЭЦВМ сводятся к выполнению арифметического сложения и небольшого числа простых вспомогательных операций (сдвиг числа, обращение кода числа) [42, 43]. В некоторых конструкциях ЭЦВМ используются и вычитающие устройства.

Сумматоры и вычитающие устройства строят из одноразрядных суммирующих и вычитающих схем.

Одноразрядная суммирующая схема производит суммирование трех одноразрядных чисел, первые два из которых представляют слагаемые, а третье - перенос из соседнего младшего разряда. На выходе одноразрядной суммирующей схемы выдается результат в виде двухразрядного числа, выраженного в той же системе счисления, причем одна из цифр результата является суммой данного разряда, а вторая - переносом в следующий старший разряд.

В практике построения ЭЦВМ суммирующее устройство обычно собирают из двух полусумматоров. Каждый из полусумматоров выполняет правила двоичного сложения цифр, которые проще всего выражаются при помощи табл. 5.4.

Таблица 5.4

Из таблицы легко можно видеть, что для простого двоичного сложения, выполняемого полусумматором, можно написать соответствующие функции алгебры логики: сумма = XȲ ∨ X̄Y; перенос = XY, где X и Y - входные сигналы данного разряда в первом и втором слагаемых. Приставка "полу" использована в связи с тем, что для получения правильной цифры числа, представляющего сумму первого и второго слагаемых, необходимо еще прибавить сигнал переноса из соседнего младшего разряда. Учитывая, что правила для переноса точно такие же, как и правила табл. 5.4 для сложения цифр первого и второго слагаемых, для этой цели можно использовать второй полусумматор. Таким образом, для сложения двух чисел требуется по крайней мере по два полусумматора на разряд, за исключением самого младшего разряда. В действительности необходимо намного больше оборудования, чем по два полусумматора на разряд, ибо сигнал переноса может быть получен от любого из полусумматоров и нужно обеспечить передачу любого из этих двух переносов в следующий старший разряд.

В связи с этим при синтезе суммирующего устройства из нейронных элементов целесообразно строить сразу полный сумматор, представляющий функциональное устройство, на вход которого по-даются слагаемые (Х_k и Y_k) и перенос из предыдущего разряда (Π_k-1), а на выходе выдаются сумма (Σ_k) и перенос в следующий старший разряд (Π_k). Правила работы полного сумматора (для A-того разряда) можно представить в виде табл. 5.5.

Правила двоичного сложения для полного сумматора, записанные в табл. 5.5, могут быть выражены при помощи формул алгебры логики:

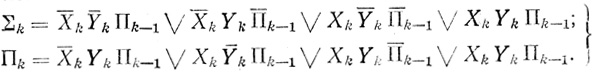(5.11)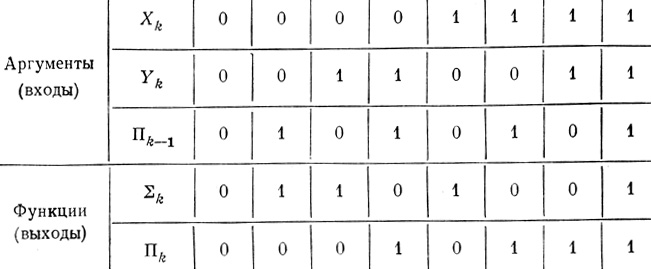

Таблица 5.5

Синтез надежной нейронной сети, реализующей заданную логическую функцию, начинается со сведения последней к совершенной дизъюнктивной нормальной форме (СДНФ) в виде одной идеальной диаграммы Венна (см. § 4.5). В данном случае формулы 5.11 уже записаны в СДНФ, и поэтому идеальные вероятностные диаграммы для Π_k и Σ_k могут быть записаны (рис. 5.9) без применения таблиц, непосредственно по формулам или табл. ,5.5. В последнем случае наборы единиц и нулей в строчках таблицы для суммы и переноса принимаются за содержимое ячеек диаграммы D^ρ̄ в порядке возрастания их номеров от нулевого до (2ⁿ- 1).

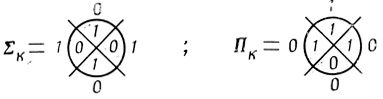
Рис. 5.9

Три разряда полного сумматора, построенные из диаграмм типа D^ρ̄, показаны на рис. 5.10.

Для построения сумматора из ненадежных нейронов идеальные вероятностные диаграммы для Σ_k и Π_k по правилам, изложенным в § 4.5, заменяем сетями ненадежных вероятностных диаграмм (рис. 5.11). После этого производим последовательный переход к сетям порядковых (рис. 5.12) и пороговых D^θ_r,i диаграмм (рис. 5.13)" Правила этого перехода описаны в § 4.7.

Одновременно с построением сети пороговых диаграмм определяются допустимые диапазоны изменений порогов Θ_r,i ∈ β {β₁,... ...,β_k}, не приводящие к искажению вычисляемой функции. Теперь по каждой из пороговых диаграмм D_r,i^θ (рис. 5.13) необходимо синтезировать формальный нейрон.

Потребуем, чтобы все формальные нейроны, входящие в сети, вычисляющие Σ_k и Π_k, были оптимальны, т. е. имели минимальное число волокон и ветвей одновременно. В отдельных случаях будем допускать вхождение в схемы нейронов, минимальных по числу ветвей V̂ и имеющих относительный минимум волокон W̃. Для синтеза оптимальных нейронов по пороговым диаграммам воспользуемся методами линейного программирования (см. § 3.4) и автоматического перебора на ЭЦВМ (см. § 3.7). В результате получаем две надежных нейронных сети, состоящие из оптимальных формальных нейронов: сеть, вычисляющую цифру суммы Σ_k (рис. 5.14), и сеть, вычисляющую цифру переноса Π_k (рис. 5.15).

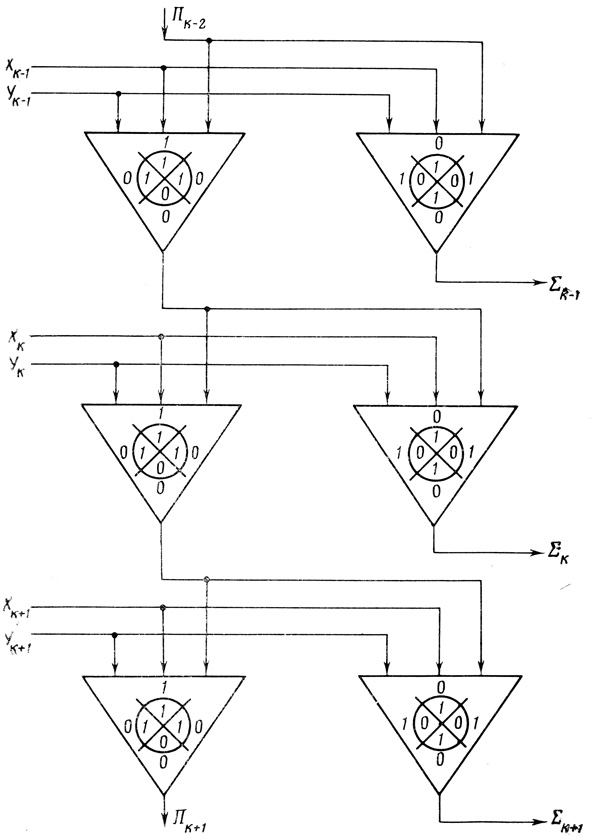
Рис. 5.10

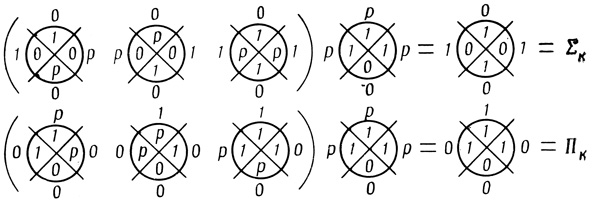
Рис. 5.11

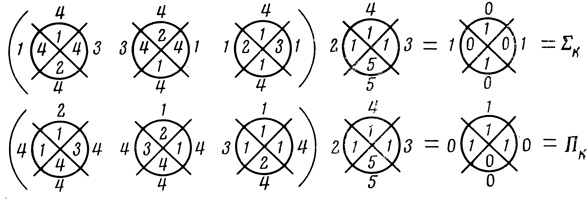
Рис. 5.12

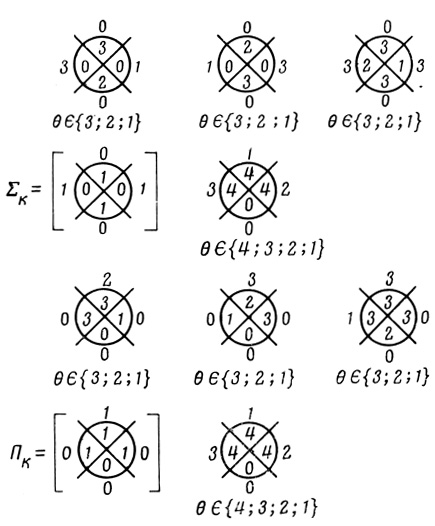
Рис. 5.13

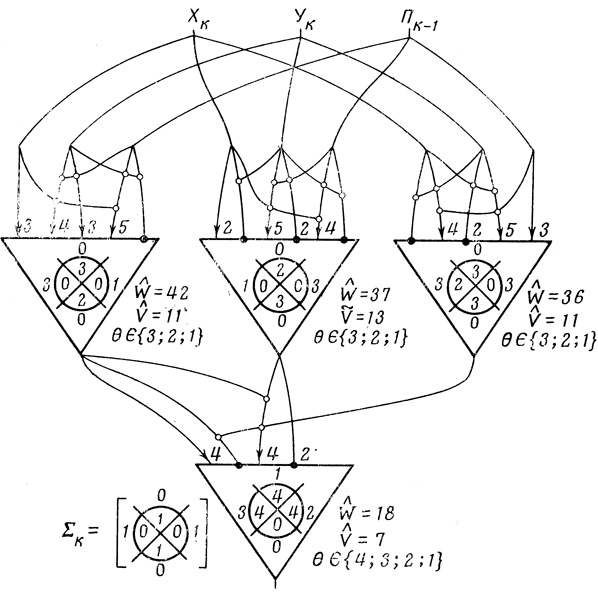
Рис. 5.14

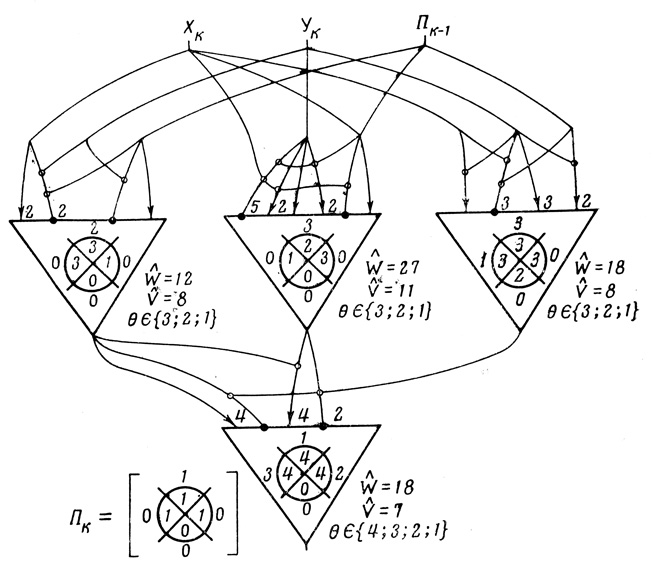
Рис. 5.15

Для построения m-разрядного сумматора необходимо использовать m схем для Σ_k и столько же схем Π_k. Таким образом, m-разрядный сумматор должен состоять из 8m формальных нейронов. Из рис. 5.14 и 5.15 видно, что пороги нейронов первых рангов схем для Σ_k и Π_k могут принимать три значения, а пороги вторых рангов четыре значения. Если какая-либо техническая реализация нейронов, предназначенных для сумматора, имеет больший разброс пороговых значений, то число рангов g может быть увеличено. Это, естественно, вызовет увеличение необходимого числа нейронов, которое в общем случае для m-разрядного двоичного сумматора составит величину 2m (3g-2).

Зная правила функционирования нейронных сетей, легко убедиться, что при любых независимых флуктуациях порогов в отдельных нейронах (в определенных диапазонах изменений 0) сеть в целом выдает Σ_k и Π_k безошибочно. Это позволяет ожидать от технической реализации сумматора из нейронных элементов высокой надежности работы: отсутствия на выходе сбоев, компенсации (за счет логической избыточности нейронных сетей) разброса параметров элементов при производстве за счет старения, воздействия внеш-ней среды (температуры, влажности, радиации и т. п.). В дальнейшем необходима всесторонняя теоретическая и экспериментальная проверка надежности устройств, синтезированных с использованием изложенных принципов.

Рассмотрим еще один пример возможного использования надежных нейронных схем для построения отдельных устройств ЭЦВМ. В некоторых из цифровых машин применяются вычитающие устройства. При вычитании одного числа из другого каждая цифра уменьшаемого делается меньше на величину соответствующей цифры вычитаемого, и если при этом цифра уменьшаемого становится меньше нуля, то из следующего старшего разряда "занимается" единица. Правила двоичного вычитания приведены в табл. 5.6.

Прибор, который, имея на входе уменьшаемое и вычитаемое, выдает на выходе разность и заем в соответствии с табл. 5.6, называется полувычитающим устройством. В терминах булевой алгебры функции его таковы: разность = XȲ ∨ X̄Y, заем = X̄Y, где X и Y - цифры уменьшаемого и вычитаемого в данном разряде.

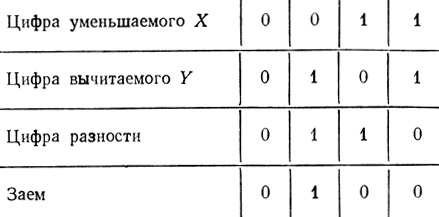
Таблица 5.6

Для построения полного вычитающего устройства необходимо реализовать трех входовую двух выходную схему в соответствии с табл. 5.7, где X_k - цифра уменьшаемого в данном разряде; Y_k - цифра соответствующего разряда вычитаемого; Z_k-1-заем из соседнего младшего разряда; Z_k - заем из соседнего старшего разряда; U_k- разность.

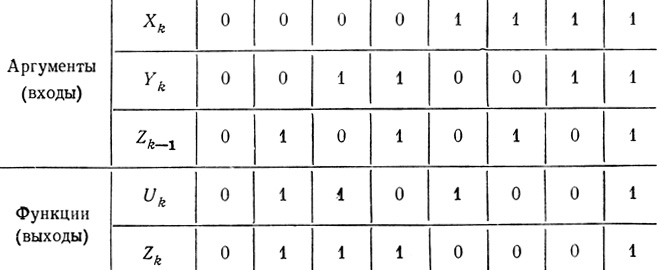
Таблица 5.7

Функции полного вычитающего устройства в терминах исчисления высказываний таковы:

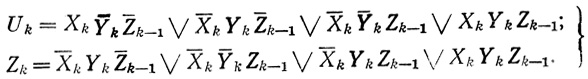(5.12)

Построив по формулам (5.12) или непосредственно по табл. 5.7 совершенную дизъюнктивную нормальную форму функции U_k и Z_k (рис. 5.16), убеждаемся в том, что идеальные диаграммы D^ρ̄ для разности U_k и суммы (рис. 5.9) тождественно совпадают (разумеется, если не считать того, что в первом случае переменными являются уменьшаемое, вычитаемое и заем из соседнего младшего разряда, а во втором - слагаемые и перенос из соседнего младшего разряда). В связи с этим для получения разности U_k при построении k-того разряда полного вычитающего устройства можно использовать надежную нейронную сеть, ранее синтезированную для вычисления суммы Σ_k (рис. 5.14).

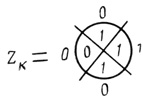
Рис. 5.16

Для синтеза схемы, вычисляющей заем Z_k из соседнего старшего разряда, пользуясь правилами, изложенными в главе 4, последовательно построим вероятностную D^ρ_r,i, (рис. 5.17), порядковую D^π_r,i (рис. 5.18) и пороговую D^θ_r,i (рис. 5.19) сети диаграмм. По каждой из пороговых диаграмм последней сети методами линейного программирования и автоматического перебора (см. § 3.4-3.7) синтезируем формальные нейроны (оптимальные, либо с минимальным числом ветвей V̂ и относительным минимумом волокон Ŵ ). В результате получаем нейронную надежную сеть для вычисления величины заема Z_k из соседнего старшего разряда (рис. 5.20). Таким образом, сочетание схем для Σ_k и Z_k дает разряд полного вычитающего устройства.

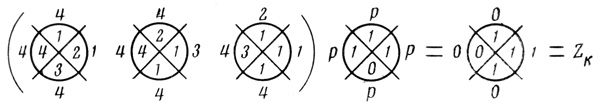
Рис. 5.17

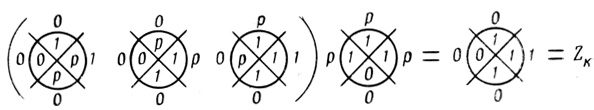
Рис. 5.18

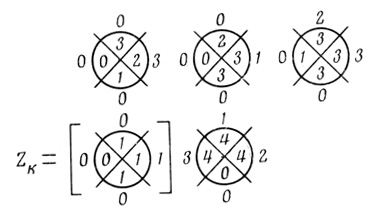
Рис. 5.19

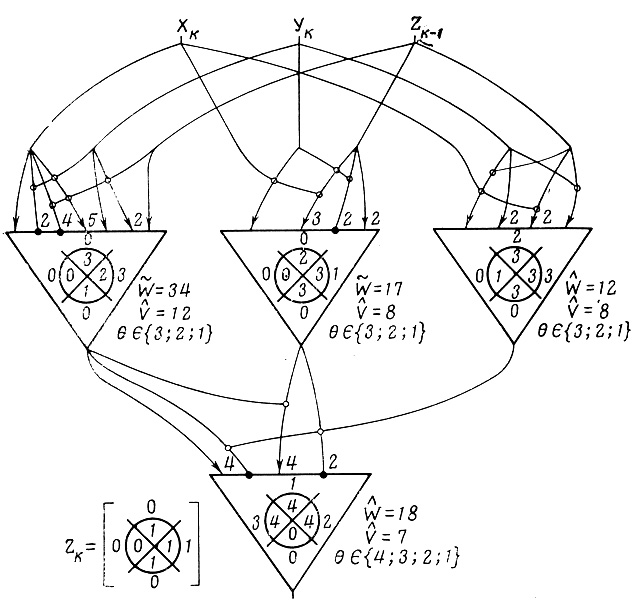
Рис. 5.20

Аналогичными методами можно было бы синтезировать и ряд других устройств арифметических узлов ЭЦВМ (для умножения, деления и т. п.). Однако принципиальный интерес представляет построение из надежных нейронных сетей запоминающих устройств. В настоящее время методики такого построения не разработаны. Однако кое-какие предпосылки, позволяющие предполагать возможность реализации памяти на нейронных сетях, имеются. В частности, можно предполагать, что решение этой задачи будет найдено при дальнейших исследованиях нейронов и нейронных сетей с обратными связями.