§ 5.3. Синтез триплетов для выполнения логических операций и оценка их надежности

В § 4.3 был изложен метод синтеза надежных сетей при помощи карт стабильности. Здесь рассмотрим предложенное Майтра [36, 37] применение этого метода для повышения надежности выполнения логических операций.

Предположим, что триплет конструируется из двух входовых модулей, собранных на диодах и сопротивлениях и выполняющих операции "и" и "или" (рис. 5.8).

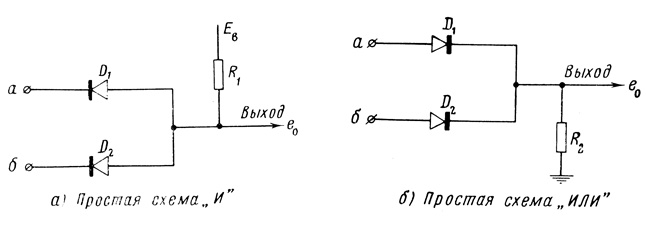
Рис. 5.8

Простой триплет первого порядка обозначим через Т₁ и будем считать, что три элементарные ячейки, из которых он состоит, являются триплетами Т₀ нулевого порядка. Будем полагать, что в элементарных схемах Т₀ (рис. 5.8) вероятностью отказа сопротивлений можно пренебречь, так что функционирование их зависит от вероятности обрыва Р₀ и вероятности короткого замыкания Р₃ в каждом из диодов.

В связи с тем, что отказы диодов изменяют векторы надежности и функциональный, Майтра предложил то функциональное состояние, для которого предназначен модуль, назвать преобладающим состоянием модуля. Естественно потребовать, чтобы преобладающему состоянию модуля соответствовала наибольшая составляющая его вектора надежности.

Для анализа надежности триплетов определим возможные функциональные состояния их модулей Т₀ и соответствующие им вероятности (табл. 5.2). Из этой таблицы непосредственно можно определить вероятности каждого из возможных состояний, обусловленные отказами всех видов. Вероятности эти будем обозначать буквами Р с индексом, соответствующим в табл. 5.2 определенному состоянию ячейки.

Тогда вероятности состояний для ячейки "и" будут

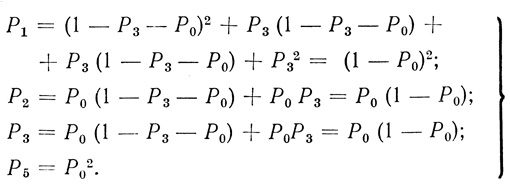(5.5)

Отсюда видно, что

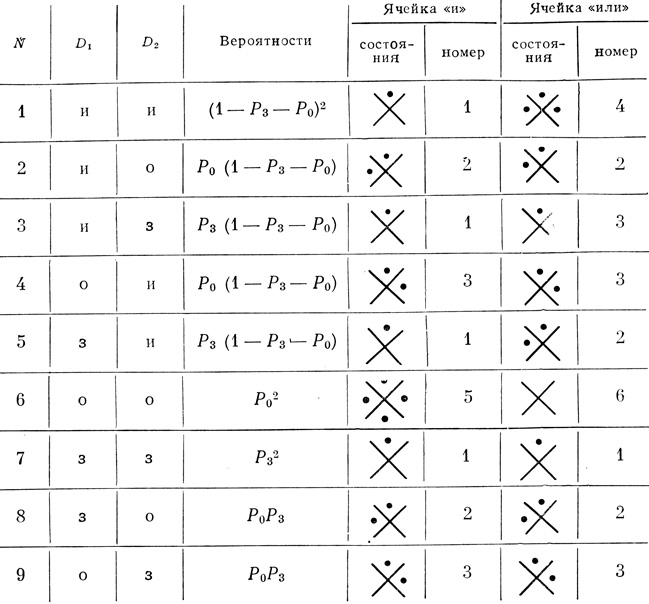
Таблица 5.2

Вероятности состояний для ячейки "или" будут

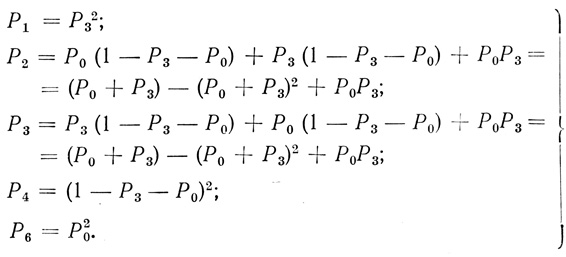(5.6)

В этом случае, как и в предыдущем, Р₂ = Р₃ и Р₁ + P₂ + Р₃ + Р₄ + Р₆ = 1. Изменение надежности триплета зависит от закона распределения возможных логических состояний его элементов. Для того чтобы достичь увеличения надежности триплета (по сравнению с надежностью элемента), необходимо исследовать различные логические состояния элементов при соответствующих условиях функционирования. При дальнейших исследованиях более сложных схем, содержащих формальные нейроны со всеми видами волокон, необходимо определить связь вектора надежности с возможными значениями порогов и соответствующими им функциональными состояниями.

Обозначим через X_jn функцию вероятностей, соответствующую j-тому состоянию общего функционального вектора триплета n-го порядка Т_n, предназначенного для выполнения операции "и". Тогда, используя (5.5) и полагая Р₃ = Р₀, для вероятностей состояний элементарного модуля "и" имеем

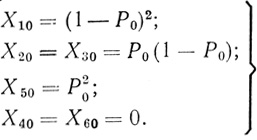(5.7)

Вероятности Х₄₀ и Х₆₀ приняты равными нулю потому, что соответствующие им состояния в табл. 5.2 для ячеек "и" отсутствуют.

Аналогично через Y_jn обозначим функцию вероятностей, соответствующую j-тому состоянию общего функционального вектора триплета n-го порядка Т_n, предназначенного для выполнения операции "или". Используя (5.6) и полагая Р₃ = Р₀, получаем

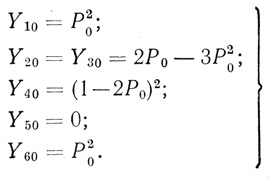(5.7)

Теперь для получения более надежной ячейки "и" необходимо правильно выбрать преобладающие состояния ячеек F₁, F₂ и F₃ (рис. 4.10). Выбор производится при помощи карт стабильности и надежности (§4.3).

Анализ, проведенный Майтра [36], показал, что для получения функции "и" в качестве преобладающих состояний ячеек F₁ и F₂ целесообразно выбрать элементы "и". Что касается ячейки F₃, то интересно рассмотреть влияние выбора ее на надежность триплета. Для этого составим карту надежности (табл. 5.3), общую для случаев, когда ячейка F₃ в качестве преобладающей выполняет функцию "и" и когда выполняет функцию "или". Непосредственно

из карты надежности суммированием соответствующих выражений условной вероятности можно составить функцию Х_n:

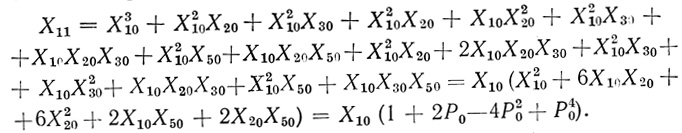(5.9)

Из (5.9) легко видеть, что для всех 0 < Р ≤ 0,5 выражение в скобках всегда больше единицы. Следовательно, надежность триплета, выполняющего операцию "и", выше, нежели надежность элементарной ячейки "и".

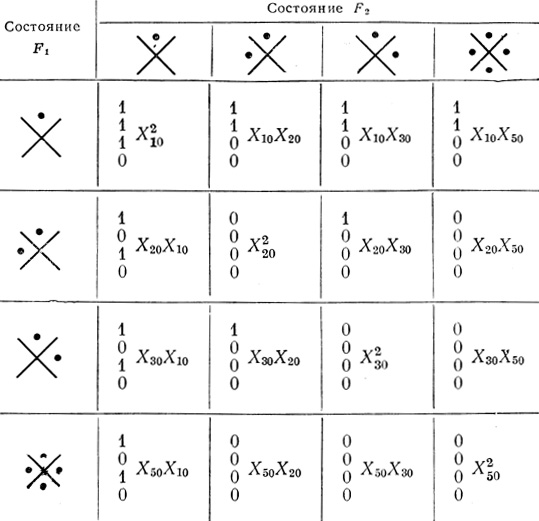
Таблица 5.3

Другое дело, если для элемента F₃ в качестве преобладающей выбрать функцию "или". Из той же карты надежности (табл. 5.3) для Х₁₁ имеем

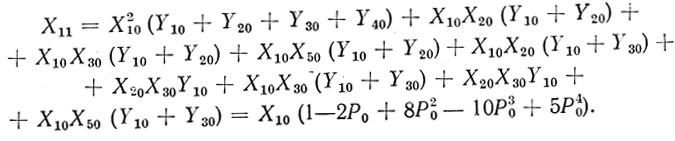(5.10)

Легко видеть, что в этом случае для всех 0 < Р ≤ 0,5 в скобках находится величина, меньшая единицы. Следовательно, неудачный выбор элемента F₃ привел к нежелательному результату: надежность триплета ниже надежности простого элемента "и". Аналогично этому можно показать, что для построения триплета "или" с точки зрения увеличения надежности целесообразно элементы F₁, F₂, F₃ выбрать с преобладающим функциональным состоянием "или".

Майтра исследовал триплеты порядка выше первого, т. е. такие, элементами которых являются также триплеты, но на один порядок ниже [36]. При этом основное внимание было обращено на исследование изменения надежности, вызванное повышением порядка триплета. Оказалось, что при увеличении n > 1 выигрыш в надежности достигает своего верхнего предела при определенном значении n (при достаточно малом Р₀, X_1n, Y_1n достигают максимума при n = 3), после чего рост n приводит к уменьшению надежности.

Изложенный метод синтеза и вычисления надежности может быть распространен на более сложные структуры из нейроподобных элементов. Однако на этом пути имеются существенные трудности, связанные с выявлением всех функциональных состояний системы, определяемых изменениями порогов и отказами каждого из элементов.