Математические модели центральной нервной системы. Г. Д. Ландаль. Чикагский университет, Чикаго, Иллинойс

Нам представляется уместным обсудить здесь некоторые из применений математики к исследованию центральной нервной системы. С этой целью мы выберем ряд различных проблем; некоторые из них были исследованы несколькими способами. Для того чтобы осветить достаточное число вопросов, ограничимся лишь рассмотрением того, как математически формулировать конкретную модель. Здесь мы сможем только указать требуемое решение и обратить внимание на те вопросы, ответы на которые дает эта модель, а также на успехи, достигнутые с ее помощью в объяснении известных фактов и в развитии новых представлений.

Выбор применяемого математического аппарата будет определяться, естественно, характером исследуемого явления. Существует ряд явлений, в которых проявляются свойства "поля". Некоторые из-этих явлений могут быть описаны с помощью специальных определений, которые подсказывают применение того или иного математического метода. В то же время многие явления более естественно описываются на основе понятия нервных сетей, свойства элементов которых приближаются к свойствам изолированных нейронов. Даже сравнительно простые сети позволяют описывать случаи весьма сложного поведения. Поэтому обычно использовался именно этот подход. Кроме того, определенные свойства полей выявляются здесь вполне естественно.

Электрический импульс после возникновения в нейроне А распространяется по аксону этого нейрона и достигает синапса, т. е. окончания аксона на нейроне В. Здесь импульс исчезает, но вызывает при этом изменения в нейроне В. Если эти изменения достаточно кратковременны, то к моменту прихода второго импульса из аксона А на нейрон В не остается никакого следового возбуждения. Может оказаться, что в этом случае не произойдет суммирования возбуждения во времени. Поэтому если первый импульс не способен вызывать ответный импульс в нейроне В, то два или более последовательных импульсов также не смогут сделать это. Но если при этом одновременно с импульсом от нейрона А приходит импульс от другого нейрона A', то нейрон В может дать разряд, т. е. генерировать импульс. Но здесь будет иметь место генерирование лишь одного импульса и только при условии, что импульсы от A и A' приходят почти одновременно. Однако если остаточное возбуждение в нейроне В сохраняется дольше, то станет возможным суммирование возбуждений, и один входной импульс вызовет несколько ответных. Очевидно, эти два случая можно рассматривать отдельно [22].

Рассмотрим первый из них и допустим, что время может быть квантовано в единицах, наиболее удобных для описания скорости протекания процессов возбуждения. Для удобства допустим также, что импульсы от нейронов А, А',... оказывают одинаковое влияние на нейрон В. Назовем порогом возбуждения θ нейрона В число одновременно приходящих импульсов, необходимых для возбуждения этого нейрона. Если θ=1 и на нейроне В оканчивается только аксон нейрона А, то мы можем утверждать, что нейрон В будет давать разряд в момент t+1 тогда и только тогда, когда нейрон А дает разряд в момент t. Если же θ = 1, а на нейроне В оканчиваются аксоны нейронов А и А', то мы можем утверждать, что нейрон В даст разряд в момент t+1 тогда и только тогда, когда нейроны А или А' или оба вместе дают разряды в момент t. При θ = 2 мы можем утверждать, что нейрон В даст разряд в момент t+1 тогда и только тогда, когда нейроны А к А' одновременно дают разряды в момент t. Если допустимы тормозные влияния и если нейрон А' оказывает тормозное влияние при θ=1, то утверждение "нейрон В дает разряд в момент t+1" будет истинным, если утверждения "нейрон А дает разряд в момент t" и "нейрон A' не дает разряда в момент t" оба истинны. Таким образом может быть установлено соответствие между некоторой нейронной сетью и множеством логических высказываний. Справедливо и обратное утверждение: по заданному множеству высказываний может оказаться возможным построить соответствующую нервную сеть, и тогда возникает ряд вопросов. Например, что произойдет, если в сети окажутся замкнутые контуры? При каких условиях может быть определена сеть, соответствующая данному множеству логических высказываний, и при каких условиях может быть дана ее каноническая форма, если решение существует? К чему приведет отказ от предположения о дискретности времени? Для более детального ознакомления с перечисленными выше и связанными с ними проблемами читатель отсылается к статьям [29, 23, 24, 5, 14, 50, 48]. Некоторые попытки применить результаты указанных работ к проблемам психологии были сделаны Рашевским (см. [40]), который рассматривал, например, проблему логического обоснования, исходя из моделей нервных сетей. Ряд вопросов, связанных с решением проблемы устойчивости, затрагивается в работе [53].

Помимо ограниченных сетей, интерес для исследования представляют также сети со случайными связями [46]. Если группа растущих нейронов посылает аксоны беспорядочным образом (если не учитывать смещений или небольших ограничений), то образовавшуюся сеть можно количественно охарактеризовать вероятностью возникновения замкнутых контуров и цепей различной длины. Можно попытаться вычислить эти вероятности, рассчитать состояние системы при заданных уровнях беспорядочных входов или определить условия, при которых такие сети могут приходить в состояние возбуждения [39]. Можно также найти условия, при которых возможно распространение импульсов в некоторой совокупности нейронов со скоростью, которая может быть вычислена как функция параметров системы [1].

Можно учесть вероятность образования функциональных групп клеток в пределах беспорядочной нейронной сети при определенных условиях [31, 51]. Естественно допустить, что возбуждение, возникшее в точке х' сети, окажет влияние на нейроны в точке х, которое можно описать убывающей функцией расстояния между точками х' и х, т. е. Q(x, x'). В устойчивом состоянии возбуждение в точке х, а именно ε(х), может быть выражено суммой внешнего воздействия f(x) и воздействия от всех других областей самой сети. Последнее выражается интегралом выходов других областей, взвешенных посредством функции θ. Но выход в точке х можно рассматривать как заданную функцию φ[ε(x')] возбуждения ε в точке х', зависящую от свойств нейронов. Следовательно, мы имеем

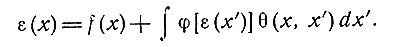
(1)

Если функция θ(х, х') зависит также от числа случаев одновременного возбуждения нейронов в точках х и х', происшедших в прошлом, т. е. от степени предварительного обучения, то становится возможным локальное развитие функциональных групп. Две такие группы могут иметь некоторые общие элементы. Эти группы могут периодически становиться автономно активными, образуя при этом пути для временной памяти. Сначала, в процессе формирования, такие группы трудно собрать, но потом трудно вызвать их распад. Соседние группы стремятся тормозить друг друга [51].

Затронем теперь проблемы, возникающие при изучении сетей из элементов, к которым можно применить непрерывную модель [40]. При определенных условиях, когда второй нейрон имеет достаточно большую постоянную времени (период остаточного возбуждения), мы можем считать, что изменения в состоянии возбуждения ε данного нейрона В, например изменения поляризации, происходят со средней частотой v поступления импульсов от его соседей. Это состояние возбуждения в свою очередь определяет частоту на выходе, которую для заданной модели можно вычислить. С этой точки зрения достаточное приближение дается уравнением

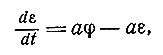
(2)

где а обозначает постоянную скорости восстановления состояния, а φ пропорциональна сумме частот v_i всех входных импульсов до момента достижения порога возбуждения h. Элемент сети может представлять собой также сенсорное (чувствительное) окончание, если φ есть функция, относящая интенсивность S внешнего раздражения к изменению электрических свойств данного элемента. В общем случае по ряду причин надо полагать, что выход определяет не величина ε, а ε - j, где j - тормозное влияние или явление адаптации. В простейшем случае значение j определяется аналогично значению ε в приведенном выше уравнении, т. е.

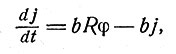
(3)

где b и Rφ соответствуют а и φ.

Уравнение (2) объясняет большинство экспериментальных результатов, полученных при изучении слухового порога. Для тестовых тонов относительно небольших частот полоса последних должна выбираться достаточно узкой. Пороги для периодически изменяющихся тонов исследовались в работе [2].

Рассмотренные выше модели даже простейших сетей могут объяснить достаточно много явлений. Например, рассмотрим цепь из двух элементов А и А', причем пусть А представляет чувствительный элемент, подчиняющийся приведенной выше паре уравнений, в которых φ есть монотонно возрастающая функция от S, и пусть А' - реагирующий элемент. Для простоты примем, что элемент А' имеет параметры R' = 0, а'>>а, b и порог h' и реагирует просто на превышение порога h', вызываемое выходом первого элемента. Если теперь к элементу A, имеющему параметры R<1 и а>b, внезапно приложить раздражение постоянной силы, то, как видно из этих уравнений, интенсивность ответной реакции, начавшейся после короткой задержки, сначала увеличится, а затем упадет до некоторого постоянного уровня, зависящего от интенсивности 5 приложенного раздражения. Этот тип реакции подобен реакции "непрерывно функционирующих" зрительных элементов. Однако при R=1 и b>a во время раздражения никаких ответов обнаружено не будет, но при внезапном прекращении раздражения появится кратковременный ответ. Подобным образом ведут себя в глазу элементы, реагирующие на выключение. В обоих случаях возможно рассчитать время, необходимое для возникновения реакции после нанесения или после прекращения раздражения. Это время будет зависеть от S, причем между интенсивностью раздражения и временем до начала реакции имеется простая зависимость, совпадающая с экспериментальными данными [13].

Вычисление отношения 6 интенсивности реакции в конце периода освещения при данной частоте а смены света и темноты к интенсивности ответа при f = ∞ дает соотношение

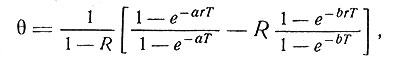
(4)

где T=1/f, а к - часть периода Т, приходящаяся на фазу "освещения". Приведенное выражение довольно хорошо совпадает с экспериментально определенными зависимостями θ от r и T (см. [13]).

Аналогичным образом в случае R = 1 и a>>b получается выражение для условий, при которых реакция просто не происходит. Уменьшение частоты будет приводить к возникновению ритмической реакции. Таким образом, мы можем говорить о частоте, которая уже не вызывает реакции, как о критической частоте мерцаний и определить эту частоту как функцию экспериментальных параметров r и S. Этот результат совпадает также со многими экспериментальными данными [13, 17].

Если на элемент, имеющий параметры R=1 и a>b, мы подаем раздражение S(t), интенсивность которого за время 1/b изменяется незначительно, то из уравнений (2) и (3) следует, что через время t>>1/bb результирующий выход будет приближаться к

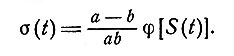
(5)

Следовательно, выход за пределы весьма короткого интервала времени, следующего за резким изменением, зависит от скорости изменения интенсивности входного разряжения, если эта скорость не слишком велика.

Легко показать, что если два элемента образуют замкнутую цепь, то достаточно интенсивное раздражение при определенных условиях может вызвать длительно сохраняющееся состояние активности. Такие пары элементов полезны при моделировании механизма адаптации. При некоторых условиях вместо постоянной активности возникает осциллирующая активность, похожая на физиологический процесс, связанный с чесательным и дрожательным рефлексами.

Если мы рассмотрим две цепи из двух нейронов, одна из которых или обе могут получать коллатераль от другой, то мы увидим, что такие простые сети обладают свойствами, напоминающими ряд физиологических явлений. Если, например, мы рассмотрим симметричное положение, в котором первый нейрон каждой цепи посылает тормозную коллатераль ко второму элементу другой цепи, то мы можем получить ситуацию, в которой возникает только одна реакция, обусловленная цепью, получающей более сильное раздражение. Поскольку степень возбуждения представляется частотой следования импульсов, здесь будут флуктуации стохастической природы. В установившемся режиме они будут иметь дисперсию, пропорциональную квадратному корню из этой частоты. Могут быть и дополнительные флуктуации, которые не зависят от интенсивности раздражения. Мы можем использовать эту простую сеть для моделирования того случая, когда имеет место различение интенсивности раздражения. В этих случаях человек или животное делает выбор между двумя или несколькими раздражителями. Если порогом раздражения вторых нейронов можно пренебречь, то результат будет похож на тот, который имел место в случае различения двух категорий раздражителей, в то время как при равенстве порогов ими нельзя пренебречь; мы имеем случай различения трех категорий раздражителей, при котором допускается невозможность выбора. Сравнение предсказаний поведения на основе такой модели с экспериментальными данными указывает на то, что эта модель вполне удовлетворительна в данном диапазоне интенсивности раздражения. И хотя в случае зрительных раздражений результаты можно объяснить для нескольких порядков величины, эта модель оказывается плохой, если попытаться с ее помощью объяснить результаты во всем диапазоне физиологических явлений.

Мы можем обобщить эту модель на раздражители более чем одной модальности. Возникают два возможных направления эксперимента. В первом из них может быть достигнуто предпочтение, причем выбор определяется тем, как испытуемый оценивает значения модальностей: В этом случае такая простая модель предсказывает, что экспериментальные результаты должны определять плоскость в многомерном евклидовом пространстве. Во втором направлении эксперимента при предъявлении двух пар раздражителей испытуемому предлагается решить, которая из этих двух пар содержит элементы, более отличные друг от друга. В этом случае можно ожидать, что полученные результаты дадут возможность определить геометрию изучаемого таким способом психологического пространства. Если мы имеем дело с такой простейшей моделью, где нет никакого взаимодействия между модальностями, то мы обнаруживаем, что "расстояние" между двумя раздражениями (S₁, S₁') и (S₂, S₂') будет задаваться выражением вида a|S₁ - S₁'| + b|S₂ - S₂'| для случая, когда имеются только две модальности. Есть данные, указывающие, что это соответствует действительности, по крайней мере в некоторых случаях. Например, полученное пространство будет евклидовым только для специальных сетей. В этом случае можно установить методы оценки размерности пространства, соответствующего некоторой совокупности данных [54]. Здесь следует обратиться к работе [30] о вероятностной геометрии, которая возникла отчасти при изучении явлений различения предъявляемых раздражений.

Вернемся снова к взаимосвязанной паре нейронных цепей. Теперь будем считать, что у первого элемента каждой цепи a>b, R = 1, и эти элементы одинаковы. Пусть для перекрестных связей, обозначаемых штрихами, a'<b', R'=1, и пусть a = b', b = a'. Если к обеим цепям одновременно прикладывать одинаковое раздражение, то никакой реакции не последует. Но если одно раздражение приложено после другого, то реакция появится, причем раздражение "передвигается" от одной цепи к другой, и в данный момент возбуждает только одну цепь. Этот тип поведения цепей подсказывает возможность использования подобных "элементов в моделях, объясняющих восприятие истинного или кажущегося движения.

В формальной модели реакции на движение в работе [42] вводится принцип автокорреляции. Там рассматривается два параллельных канала связи между парой - рецепторов и парой эффекторов. Каждый канал состоит из дифференцирующего, инерционного и перемножающего элементов, причем от каждого дифференцирующего элемента идет связь к перемножающему элементу противоположного канала. Когда возбуждение движется таким образом, что сначала возбуждается один канал, а затем другой, то сильно коррелированными могут быть только те сигналы, которые появляются на выходе первого. Выход рассчитывается последовательным преобразованием входного сигнала последовательными операторами. Величина реакции может быть вычислена как функция скорости движения возбуждения. Она имеет максимум и стремится к нулю, когда эта скорость стремится к нулю или к бесконечности.

Аналогичные соотношения между выходом и скоростью движения возбуждения очень просто могут быть получены в результате анализа подобных нейронных сетей, обладающих свойствами, которые мы рассмотрели выше [48]. Кроме того, эту модель естественно обобщить а линейную или двумерную совокупность элементов, в которой число связей у взаимодействующих коллатерарей уменьшается с расстоянием. Мы можем рассмотреть, то произойдет, если небольшое раздражение приложить а короткое время к одной области, а после определенной задержки - к другой области, расположенной на некотором расстоянии. Такой характер возбуждения имеет место, когда возникает явление "кажущегося движения". Показано, что некоторые стороны этого явления при количественном рассмотрении близко соответствуют результатам, полученным на модели [19]. Таким образом, мы видим, что можно ожидать появления достаточно сложных эффектов даже при таких простых схемах соединений, какие могут наблюдаться в сетчатке глаза [26].

Небольшая модификация описанной выше сети позволяет перейти к механизму для обнаружения кривизны траектории движения. Имеются указания на то, что хотя глаз и не

следует за воспринимаемой контурной линией, но наблюдаемые движения глаз могут быть совокупностью следящих движений и более или менее случайных движений [41, гл. 16]. Представленные ниже результаты, полученные в данном случае, вероятно, можно применить к зрительному восприятию контуров.

Для простоты предположим, что движение глаза осуществляется парами мышц, которые действуют в горизонтальном и вертикальном направлениях. Пусть составляющая раздражения, вызывающая горизонтальное движение (обозначим ее x' = dx/dt), возбуждает элемент H, т. е. S = x'. Пусть Н посылает коллатерали, образующие синаптические контакты с H_y и H'. Аналогично пусть вертикальное движение y' вызывает возбуждение элемента V, который образует контакты с элементами V_x×V'. Пусть далее Н_х связан с V, a V_y связан с H'. Допустим, имеется симметрия, т. е. Н и V эквивалентны, и т. д. Допустим, что элементы Н и V таковы, что мы можем пренебречь аккомодацией и что φ(S)=α'S и а очень велико, причем S есть раздражение x или y. Пусть для Н_y и V_x выполняются условия a>b и R = 1, такие, что b достаточно велико, чтобы можно было воспользоваться приближением (5). Пусть H' и V' - нейроны, реагирующие по закону "все или ничего", с порогом θ = 2. Пусть, наконец, H' и V' воздействуют на Н" и V" через такие перекрестные тормозные связи, как в рассмотренном выше случае простого различения двух категорий. Можно видеть, что для не слишком быстрого движения выходы ε_H" или ε_V" приближаются к значениям

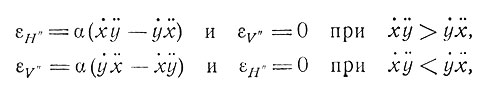
(6)

где α - константа. Если движение происходит примерно с постоянной скоростью, то значение выхода пропорционально кривизне траектории движения.

Далее мы рассмотрим по существу ту же самую структуру, которая использовалась выше для описания механизма различения, но теперь элементы нервной сети будут иметь различные параметры. Чтобы упростить дело, рассмотрим лишь устойчивое состояние. В частности, положим, что каждый из элементов некоторой двумерной совокупности слоя I образует взаимно однозначные возбуждающие контакты на элементах слоя II. Пусть каждый элемент слоя I образует такие тормозные контакты на соседних элементах, что вероятность контакта с некоторым ближайшим соседом достаточно велика, но она снижается для элементов, удаленных на расстояние, превышающее заданное расстояние δ. Пусть, например, возбуждаются элементы слоя I, лежащие внутри квадрата со стороной x>>δ. Если имеется достаточно большое число взаимных тормозных влияний, то хотя данный элемент слоя II, расположенный вблизи центра квадрата, и возбуждается от соответствующего элемента слоя I, он может не дать ответа вследствие получения большого числа тормозных импульсов от соседних элементов. Однако элементы, расположенные близко к краю контура, будут получать вдвое меньше тормозных импульсов от элементов, расположенных внутри квадрата. Следовательно, элементы слоя II, близкие к границе квадрата, могут давать реакцию, если даже элементы, которые расположены не так близко от границы, т. е. на расстоянии порядка величины δ, реакции давать не будут. Если вместо элементов внутри квадрата возбуждать элементы, лежащие вне его, то картина состояния слоя II останется в основном без изменений, хотя будет несколько более выражена. Совершенно аналогичная картина состояния слоя II может быть получена также при возбуждении только тех элементов в слое I, которые расположены очень близко к границе. Во всех этих случаях картины возбуждения слоя I различны, а соответствующие картины в слое II получаются по существу одними и теми же. Если теперь мы рассмотрим третий слой, имеющий такие же связи со слоем II, как слой II со слоем I, и в котором это взаимодействие достаточно сильно и характеризуется расстоянием δ такого же порядка, как и в других слоях, то от этого ничего нового не добавится. Но если это взаимодействие осуществляется на большом расстоянии и задается функцией K(s, s'), количественно определяющей эффективность влияния нейронов в точке s' на нейроны в точке s для каждой единицы возбуждения а в s', то возбуждение а в точке s будет задано уравнением

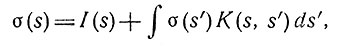
(7)

где I(s) обозначает выход слоя II вдоль контура предъявляемого образа, а ds' обозначает элемент вдоль этого контура. Для образов, размеры которых превышают расстояние δ, функция σ(s) для трех рассматриваемых образов приближенно будет одной и той же с точностью до слагаемого I. Если бы мы имели дело с произвольными образами, то зависимость функции σ(s) от формы контура выражалась бы через K(s, s'), причем σ(S) для разных форм была бы различной. Возникает вопрос об определении таких функций, как K(s,s'), чтобы разные контуры можно было легко различать с помощью некоторой функции от σ(s), например ее интеграла по контуру или ее интеграла, взвешенного функцией от s и r, где r - расстояние между s и центром тяжести образа.

На приведенном примере мы лишь проиллюстрировали, каким образом предъявляемый образ может быть разложен нервной сетью на его составные части. Рассматривались также другие механизмы, обеспечивающие инвариантность реакции по отношению к размеру, расположению образа и т. д. [40, 38]. В работах [38, 52] описан метод, которым при определенных условиях из неинвариантных свойств можно получить инвариантные. Это достигается усреднением по целой группе образов, имеющих одинаковое значение при заданном преобразовании. Здесь привлекает внимание исследование вероятностных сетей, обученных распознавать некоторые образы [6]. Такие сети будут распознавать любые другие образы только в том случае, если последние имеют какие-то общие элементы с применявшимися в процессе обучения. Проблема распознавания "общности" между различными образами, в один из которых может быть преобразован некоторый предъявленный образ, рассмотрена в работе [43].

Если на сеть (которая может содержать больше слоев) описанного выше типа воздействовать дискретными раздражителями при условии, что расстояние 6 достаточно велико, то эта сеть может избирательно пропускать только самые сильные из приложенных раздражений. Если происходят случайные флуктуации, то вероятность ответа на данное раздражение будет зависеть от интенсивности остальных раздражений. Такой механизм может служить основой для различения большого числа различных раздражителей.

Теперь перейдем к рассмотрению попыток анализа некоторых явлений восприятия цвета с помощью нейронных сетей. Сначала построим цепь, которая при небольшом числе типов рецепторов обеспечивает большое число типов реакций. Предположим, например, что имеется три типа рецепторов. Пусть рецепторы первого типа посылают волокна к точке C₁ некоторой двумерной области С, причем волокна из точки C₁ распространяются по всей области С. Пусть окончания волокон на нейронах расположены в этой области случайным образом, с тем лишь ограничением, что вероятность того, что окончание лежит в любой области, уменьшается с расстоянием от точки С₁. Допустим наличие симметрии, так что рецепторы других типов имеют коллатерали, расходящиеся от точек C₂ и С₃, причем точки С₁, С₂ и С₃ являются вершинами равностороннего треугольника.

Пусть S(λ) - распределение энергии в зависимости от длины волны, соответствующей данному цвету. Пусть S₁, S₂ и S₃ - интенсивности раздражения, необходимые для возбуждения каждого из трех типов рецепторов. Если S₁>>S₂>>S₃, то максимум возбуждения лежит вблизи точки d, тогда как при S₁ = S₂>>S₃ максимум при весьма общих условиях будет лежать посредине между точками C₁ и С₂. Пусть имеется второй слой С', нейроны которого получают возбуждающие импульсы только от соответствующих нейронов из слоя С, тогда как тормозные импульсы приходят к ним и от далеко расположенных нейронов слоя С. Тогда мы можем ожидать, как и в рассмотренных выше случаях, что возбуждение в слое С появится только вблизи той точки, которая соответствует максимально возбужденной точке в слое С'. Таким образом, может существовать поверхность, различные области которой могут возбуждаться разными цветами. При наличии самого простого типа взаимодействия и приблизительного распределения можно получить классические уравнения смешения цветов. При наложении небольших ограничений с помощью смешения трех разных цветов можно получить любой другой цвет. Надо отметить, что этот результат, который согласуется со многими экспериментальными данными, зависит не от предположения о трех типах первичных рецепторов, а от того предположения, что область С двумерна [15].

Если между фоном и рассматриваемой областью вводится взаимодействие, то можно получить результаты, совпадающие с данными эксперимента в отношении постоянства цвета. Здесь изменение наблюдаемого цвета вызывает сравнительно небольшое изменение воспринимаемого [18].

Дальнейшие интересные результаты можно получить при анализе переходных явлений. Так, например, исходя из этой модели, можно объяснить целый ряд возможных довольно заметных изменений воспринимаемого цвета [16].

Для малых интенсивностей света важную роль играет его квантовая природа. Интересно отметить, что ряд пороговых явлений можно объяснить, полагая, что глаз имеет механизмы, позволяющие ему функционировать в области максимума эффективности в соответствии с вероятностным характером этого процесса [2].

Перейдем к рассмотрению некоторых приложений вышеизложенного к проблемам обучения. Необходимой составной частью любой модели обучения является механизм, с помощью которого определенные события вызывают в ней более или менее долговременные изменения. Мы уже указывали, что сети с замкнутыми контурами можно использовать для сохранения состояния возбуждения на значительные периоды времени. Но ряд наблюдений говорит о том, что долговременные изменения должны быть совершенно стабильными, что может иметь место, если увеличить размеры области синаптических контактов или сделать их более эффективными в результате каких-либо физико-химических изменений [12, 32, 21]. В одной физико-химической модели дается естественное объяснение результата пространственных исследований, а постоянная времени связывается со скоростью обмена веществ в нейронах [21].

При выработке классического условного рефлекса животное получает некоторый раздражитель S_c, вслед за которым подается другой раздражитель S_u, например пища. После нескольких таких сочетаний условный раздражитель S_c начинает вызывать безусловную реакцию R_u (слюноотделение) даже до подачи безусловного раздражителя S_u (пища). Раздражитель S_c в результате такого процесса приобретает новое значение. Рассмотрим случай, когда при обучении требуется делать выбор. Положим, что выбор делается по-прежнему, но только теперь между двумя безусловными раздражителями, а интенсивность их воздействия изменяется в результате обучения. Будем считать, что по мере выработки условного рефлекса значение поощряемого раздражителя возрастает вместе с возрастанием числа правильных ответов. Введем некоторые допущения относительно этого процесса, добавим возможность поощрения или наказания. Тогда мы можем рассчитать вероятности того или иного ответа исходя из понятия механизма различения, аналогично тому, как мы делали это выше. Затем можно рассчитать суммарное число ошибок в зависимости от числа испытаний. Если вместо двух имеется N возможных выборов, то число N становится переменным параметром эксперимента.

Когда вероятность "правильного" ответа становится достаточно большой, она мало возрастает в ходе дальнейших испытаний, хотя интенсивность раздражителя может продолжать увеличиваться. Если испытание проводится спустя какое-то время, за которое условный рефлекс до некоторой степени угасает, то могут оказаться (ценными повторные испытания, так как добавочное возбуждение может проявляться в увеличении вероятности правильного ответа и при меньших вероятностях. Значит, естественным следствием такого подхода будет явление вспоминания [13].

Можно показать, что если исходная вероятность ответа мала, то график вероятности правильного ответа может иметь перегиб, как чаще всего и бывает на практике. Это согласуется с тем фактом, что у животного труднее вырабатывается тот рефлекс, который имеет малую вероятность спонтанного проявления [47].

Был сделан ряд интересных попыток объяснить явление обучения на основе формальных моделей [3, 4]. Например, для случая с двумя возможными исходами, вероятность одного из которых равна р, а другого (1-р), после события Е_i эта вероятность становится равной

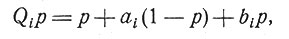
(8)

где оператор Q_i и постоянные а_i и b_i зависят от характера этого события, т. е. от того, поощрялось это событие или нет. А это событие может полностью определяться либо действиями испытуемого, либо только решениями экспериментатора, либо некоторой комбинацией этих двух возможностей. В данном случае задача состоит в том, чтобы не только определить возможный исход распределения вероятностей ответов и длительность отдельных испытаний, но и другие интересные стороны эксперимента. Этот метод можно обобщить на случай r возможных исходов путем введения матричного оператора Q_i, который применяется к вектор-столбцу, образованному из элементов p₁,... , р_r, представляющих собой разные вероятности. Этот формальный метод был с большим успехом использован для анализа ряда экспериментов. (В связи с этим интересно отметить, что теоретико-множественный подход [3] помогает связать между собой чисто формальный метод и метод, применяемый в практике психологических исследований.) Поскольку между выводами, полученными этим методом, и выводами, приведенными выше, имеются различия, интересно сравнить их лучшие стороны [22]. Интересные результаты получаются при исследовании обучения, происходящего в случайных сетях [33]. В более конструктивных моделях типа "перцептрон" способность к обучению обеспечивает возможность обобщающего восприятия [43, 44].

Далее рассмотрим механизм, входная функция которого S(t), определенная для t>0 и равная нулю при t≥T, является функцией некоторого другого параметра, а выходная функция R(t) такова, что может иметь место равенство R(t)=a'S(a"t-t'), т. е. здесь выход подобен входу, но появляется с задержкой и, возможно, имеет другой масштаб времени. Это соответствует тому, что последовательность событий на входе вызывает похожую последовательность событий на выходе, запаздывающую во времени и, возможно, идущую с другой скоростью. Один из таких механизмов может быть воспроизведен следующим образом. Пусть данный входной элемент посылает коллатераль к каждому элементу ряда, состоящего из элементов Г_i с θ = 2, каждый из которых принимает одну коллатераль также и из центра С. Пусть С при возбуждении посылает импульсы в Г_i, начиная с элемента i = 0 и кончая i = n, последним элементом ряда. Пусть Г'_i - есть совокупность элементов возбуждающего типа с постоянной времени а^-1>>Т, которые однозначно соответствуют элементам Г и возбуждаются ими. Если теперь подается раздражение S(t), интенсивность которого равна нулю при t>T, одновременно возбуждающее и С, то выход от Г' будет определяться формулой Г'_i = a'S(t), если после момента t = T выполняется равенство vi = t и vn>T, а значение Г'_i будет очень медленно изменяться во времени. Пусть каждый элемент из совокупности Г' имеет единственную коллатераль, ведущую к соответствующему элементу в совокупности Г". Пусть элементы в совокупности Г" работают согласно закону "все или ничего" с θ = 2. Пусть центр С" имеет такую же связь с совокупностью Г", как С - с совокупностью Г. Если С" возбуждается в момент времени t'<<1/a после подачи S{t), то выход из Г" будет примерно пропорционален S(t - t'). Но если скорость прохождения импульсов по Г" регулируется другими факторами, то выход будет пропорционален S(βt - t'). Заметим, что Т - длительность предъявляемого образа - не должна быть слишком большой, а время t' не может быть слишком большим, если выход хотя бы приблизительно соответствует входу.

Несмотря на то что и описанный механизм может служить определенным целям, естественно рассмотреть такие механизмы, элементы которых имеют параметры, распределенные в некоторых диапазонах. Рассмотрим механизм, аналогичный только что описанному, но допустим теперь, что центр С посылает импульсы элементам в совокупности Г одновременно, причем этот процесс поддерживается в течение некоторого времени. Пусть между центром С и элементами из Г имеются промежуточные элементы, и пусть для конкретности эти элементы будут непрерывной природы с R=1, a>>b, и пусть а будет достаточно велико. Пусть величины b этих элементов имеют распределение в широком диапазоне с функцией распределения h(b). Тогда при подаче возбуждения выход из Г будет зависеть от значений b для данного элемента из Г'. Следовательно, выход из элементов в Г, контактирующих с элементами, у которых постоянная скорости имеет величину b, определяется формулой

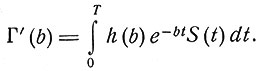
(9)

Так как по условию S(t) = 0 при t>T, то по крайней мере в определенных ситуациях этот временно сохраняющийся след может быть преобразованием Лапласа входа. Мы не будем здесь рассматривать задачу получения для выхода такой функции, которая соответствовала бы входу. Однако можно отметить, что нет необходимости в чем-то большем, чем приблизительное воспроизведение входа. Если произвольно ввести резонансные элементы, то при определенных условиях этот след представляется преобразованием Фурье. Проблема фазовых углов, так же как любое введение различия скоростей входа и выхода, усложняет воспроизведение выхода по входу.

Большая часть затронутых до сих пор положений может быть отнесена к обработке сенсорных входов или механизмов, распределяющих возбуждение по тому или иному каналу в зависимости от изменения входа во времени. Но мы можем также обратиться к процессам предварительного преобразования восприятия в нечто реальное, рассматривая их как некие элементы. В описываемой модели одна программа или функция может быть добавлена к другой или может быть включена в нее, тогда как в типичных биологических реализациях мыслительных и двигательных процессов одна схема может полностью перекрывать другую. В этом можно убедиться на многочисленных примерах, хотя мы и не умеем точно охарактеризовать это явление. Это различие, выражаясь образно, подобно различию между прямой суммой двух матриц и их кронекеровским произведением, т. е. интуитивно чувствуется, что одна структура как-то построена из составных частей, несущих отпечатки другой, возможно, таким образом, что способ построения одной группы из другой определяется некоторой группой коэффициентов. Когда младенец сосет грудь, его ручонки могут сжиматься и разжиматься в ритме движения губ. Исходя из многих аналогичных случаев, мы можем говорить, что этот процесс сосания вовлекает в движение руки, охватывая все больше и больше движений. Может быть, именно поэтому живые организмы, в отличие от машин, могут выполнять те же самые целенаправленные и сложные действия, используя любую группу эффекторов.

В описываемой модели рецепторная система вообще отделена от эффекторной. Движение живого организма может быть представлено системой последовательно усложняющихся элементарных движений. Это наводит на мысль о том, что машина, про которую в самом деле можно будет сказать, что она сознательно реагирует на воспринятое, реагировать будет вовсе не сознательно. Просто она будет в состоянии выполнять сложные действия, вроде тех, которые у животных связаны с инстинктивными реакциями.

На примере такой модели [10] анализировалась возможность представления информации в форме векторов (таких, как моды колебаний сложной системы или столбцы матрицы, представляющей структуру некоторой схемы), которые можно разложить на составляющие в различных системах координат. Эти системы понимаются как различные точки зрения на полученную информацию, причем частично эта информация в каждой системе может быть получена с помощью вероятностного механизма, аналогичного математическому описанию процесса наблюдения в квантовой механике, хотя эта модель не имеет ничего общего с квантовой физикой. Проблема состоит в том, чтобы отождествить элементы данной модели с элементами восприятия.

Ряд наблюдений над инстинктивным поведением, различные обобщения исследования процесса формирования понятий, а также ряд физиологических наблюдений, особенно в области гештальтпсихологии, говорят о глубоком содержании предположения, что сенсорные входы возбуждают некоторые реальные линейные сети, которые в свою очередь приводят к срабатыванию элементов, функционирующих по закону "все или ничего" и передающих информацию к другим сетям. В одном интересном исследовании [35] показано, какой будет геометрия реального мира в представлении организма, обладающего ограниченным числом чувств и совершенной системой логического анализа. Эти результаты относятся не только к рассматриваемым автором организмам, существующим в трехмерном пространстве; они также хорошо применимы к точкам в функциональном пространстве или к точкам в фазовом пространстве, размерность которых соответствует числу всех различных мышц и нервов, участвующих в двигательном акте. В частности, если входы описываются в терминах естественных режимов, то преобразования во внешнем мире отображаются в изоморфных преобразованиях параметров этих режимов. Обучение необходимым пространственным преобразованиям раздражителей может осуществляться на основе грубого распространения только на небольшое число режимов, так что векторное пространство системы рецепторов может иметь весьма малую размерность. Все эти идеи касаются способов достижения пространственной координации всех видов активности младенца. Они помогают понять, каким образом геометрические соотношения внешнего мира можно отобразить с помощью мышц и движений.

Мы можем считать, что устройство для распознавания образов может работать на основе предположения о том, что данный образ возбуждает те или иные виды колебаний, например электромагнитные или звуковые волны в волноводах или естественные колебания в нервной сети. Реакция будет проявляться, например, в образовании закорючек, подобных тем, которые получаются у ребенка, пытающегося рисовать квадраты [37]. Картина разных режимов может быть измерена с помощью подачи импульсов на входы при постоянном возрастании их частоты от нуля. При достижении критической или резонансной частоты в волноводе устанавливается соответствующий режим, после чего измеряются приращения мощности. Если эти значения частот или мощностей затем вводятся в некоторое анализирующее устройство (логическая сеть, перцептрон и т. д.), то работа всего этого устройства будет напоминать работу мозга.

Работа обучающейся машины может быть основана на реакции некоторой системы рычагов или ламп, в которой надо бороться с различными колебаниями и нестабильностью. Однако эти же самые колебания могут служить средством для получения ответных действий, а эти действия будут результатом потенциальных реакций, присущих данному организму.

Для случая простой линейной сети, описываемой уравнением By = x, где B - матрица дифференциальных операторов, вектор x представляет собой раздражение, а вектор y - ответ, сказанное выше означает, что реакции строятся в соответствии с решениями уравнения By = 0. Эти реакции могут быть обобщены способами, подсказываемыми этологией (Грин, не опубликовано). В качестве простого примера сопоставим два способа построения упрощенной модели лошади безотносительно к реальному животному. Согласно первому, для каждого аллюра строится сеть, задающая нужные фазовые соотношения в работе четырех (или более) моторов. Для одного аллюра конечность А может вызывать движение конечности В, но тормозить движение конечности С, а конечность С - вызывать движение конечности D через некоторый период, включающий элементы задержки, подобные синаптической задержке, и т. д. Кроме того, для выбора рабочей сети в модель вводятся переключатели. Согласно второму способу, разные аллюры описываются фазовыми соотношениями движения конечностей. При этом допускается, что каждая конечность совершает простое гармоническое колебание. Далее записывается группа чисел, выражающих средние частоты (т. е. скорости движения лошади), соответствующие заданным аллюрам, скажем 1, 2, 3, 4. Теперь остается только найти матрицу B(s) (где s - комплексная частота), строки которой ортогональны первому фазовому вектору при s = j, j = √-1 второму вектору - при s = 2j, третьему - при s = 3j и четвертому - при s = 4j. Далее надо построить сеть, соответствующую этой матрице. Теперь вместо четырех систем, связанных через коммутатор, мы получаем единую систему, не имеющую частей, которые можно было бы интерпретировать как тормозные связи, элементы задержки и т. д. Эта единая система выдает соответствующий аллюр в зависимости от скорости движения лошади.

В этом кратком обзоре мы затронули некоторые попытки изучения ряда явлений, основываясь главным образом на нейронных моделях. Мы упомянули только некоторые из множества интересных исследований, связанных с обсуждающейся тематикой. Несомненно, многие из этих исследований окажут большую помощь в понимании функций центральной нервной системы. Например, было бы очень полезно продолжать попытки интерпретировать данные о процессе слежения, представленные формальными структурами (ср. [27]), с помощью моделей, в которых более ясно введены физиологические компоненты. Сообщение Минского Д34] на дискуссии по искусственному интеллекту должно дать толчок как теоретическим, так и экспериментальным исследованиям проблем психологии. Здесь мы представили только беглый обзор некоторых моделей центральной нервной системы, и мы надеемся, что нам удалось показать, что многие интересные проблемы поддаются чарам Королевы Наук- Математики.

Литература

1. Beurle R. L., Activity in a block of cells capable of regenerating pulses, Trans. Roy. Soc. London, Ser. В (1956).
2. Bouman M. A., Sensory phenomena; Varenna conference on physicomathematical foundations of biology, New York, 1961, стр. 142-170.
3. Bush R. R., Mosteller F., Stochastic models for learning, New York, 1955. (Русский перевод: Буш Р., Мостеллер Ф., Стохастические модели обучаемости, Физматгиз, М., 1962.)
4. Bush R. R., Estes W. К., Studies in mathematical learning theory, Stanford, 1959.
5. Culbertson J. Т., A neural of behavior and of consciousness, Brown, Dubuque, Iowa, 1950.
6. Farley В. G., Self-organizing models for learned perception; Self-organizing systems, New York, 1960, стр. 7-30.
7. Goodall M. C., Performance of a stochastic net, Nature, 185 (1960), 557-558.
8. Greene P. H., Networks which realize for information representation; Symposium on the principle of self-organization, New York, 1960.
9. Greene P. H., Some biological ideas, U. S. Air Force Bionics Symposium, Dayton, Ohio, 1960.
10. Greene P. H., A suggested model for information in a computer that perceives, learns and reasons; Proc. Western Joint Computer Conference, San Francisco, 1960, стр. 151-164.
11. Hawkins J. K., Self-organizing systems - A review and commentary, Proc. IRE, 49 (1961), 31-48.
12. Hebb D. O., The organization of behavior, New York, 1949.
13. Householder A. S., Landahl H. D., Mathematical biophysics of the central nervous system, Bloomington, 1945.
14. Kleene S., Representation of events in nerve nets and finite automata; Automata studies, Annals of Mathematics Studies, № 34, Princeton, New York, I960, (Русский перевод: Клини С. К., Представление событий в нервных сетях и конечных автоматах, сб. "Автоматы", ИЛ, М., 1956.)
15. Landahl H. D., Mathematical biophysics of color vision, Bull. Math. Blophys., 14 (1952), 317-325.
16. Landahl H. D., Mathematical biophysics of color vision. II, Bull. Math. Biophys., 18 (1956); 137-149.
17. Landahl H. D., Note on the fusion frequency for stimuli of alternating duration, Bull. Math. Blophys., 21 (1959), 283-287.
18. Landahl H. D., Mathematical biophysics of color vision. Ill, Color constancy, Bull. Math. Blophys., 21 (1959), 395-402.
19. Landahl H. D., Some miscellaneous applications of neural net theory to psychological problems, Varenna conference on physico-mathematical foundations of biology, New York, 1961, стр. 295- 302.
20. Landahl H. D., A note on mathematical models for the interaction of neural elements, Bull. Math. Biophys., 23 (1961), 91- 97.
21. Landahl H. D., A model for conditioning and the effect of spaced trials in learning, Bull. Math. Biophys., 23 (1961), 159- 163.
22. Landahl H. D., Mathematical theory of the central nervous system, New York Academy of Sciences Symposium on Mathematical biology, 1961.
23. Landahl H. D., McCulloch W. S., Pitts W., A statistical consequence of the logical calculus of nervous nets, Bull. Math. Biophys., 5 (1943), 135-139.
24. Landahl H. D., Runge R., Outline of a matrix calculus for neural nets, Bull. Math. Biophys., 8 (1946), 75-81.
25. Landahl H. D., Williams С. М., Representation of modality in cutaneous sensibility, Bull. Math. Biophys., 20 (1958), 309-315.
26. Lettvin J., Maturama H. R., McCulloch W. S., Pitts W., What the frog's eye tells the frog's brain, Proc. IRE, 47 (1959), 1940-1951.
27. Licklider J. C, Quasi-linear operator models in the study of manual tracking, Developments in mathematical psychology, Glencoe, 111., 1960.
28. Luce R. D., Individual choice behavior: A theoretical analysis, New York, 1959.
29. McCulloch W. S., Pitts W., A logical calculus of ideas immanents in nervous activity, Bull. Math. Biophys., 5 (1943), 115-133. (Русский перевод: Мак-Каллок У. С, Питтс У., Логическое исчисление идей, относящихся к нервной активности, сб. "Автоматы", ИЛ, М., 1956.)
30. Menger K., Probabilistic geometry, Proc. Nat. Acad. Sci. USA, 37 (1951), 226-229.
31. Milner P. M., The cell assembly: Mark II, Psychol. Rev., 64 (1957), 242-252.
32. Milner R. M., Learning in neural system; Self-organizing systems, New York, 1960.
33. Minsky M., Selfridge O. Q., Learning in random nets, MIT Lincoln Lab., Lexington, Mass., Report № 5Y G-0024, 1960.
34. Minsky М., Steps toward artificial intelligence, Proc. IRE, 49 (1961), 8-30.
35. Nicod J., Geometry in the sensible world, Foundations of geometry and induction, New York, 1950.
36. Newell A., Shaw J. C., Simon H. A., Empirical explorations of the logic theory machine, Proc. Western. Joint Computer Conference, 1957, стр. 218-230.
37. Piaget J., Inhelder В., The child's conception of space, New York, 1956.
38. Pitts W., McCulloch W. S., How we perceive universals: the perception of auditory and visual forms, Bull. Math. Biophys., 9 (1947), 127-147.
39. Rapoport A., Ignition phenomena in random nets, Bull. Math. Biophys., 14 (1952), 35-44.
40. Rashevsky N., Mathematical biology of the central nervous system, Thales, 7 (1951), 51-68.
41. Rashevsky N., Mathematical biophysics, т. II, New York, 1960.
42. Reichardt W., Autokorrelations Auswertung als Funktions-prinzip der Zentralnervensystems, Z. Naturf., 12B (1957), 448-457.
43. Rosenblatt F., Perceptual generalization over transformation groups, S. P. Systems, New York, 1960, стр. 7-30. (Русский перевод: Розенблат Ф., Обобщение восприятий по группам преобразований, Кибернетический сборник, вып. 4. ИЛ, М., 1962.)
44. Rosenblatt F., Perception simulation experiments, Cornell Aeronautical Lab., Buffalo, N. Y., № VG-1196-G-3, 1959.
45. Selfridge O. G., Pattern recognition and modern computers, Western Joint Computer Conference, 1955, стр. 91-93.
46. Shimbel A., Rapoport A., A statistical approach to theory of the central nervous system, Bull. Math. Biophys., 10 (1948), 41-55.
47. Spence К. W., Behavior theory and conditioning, New Haven, Conn., 1956.
48. Towber J. A., A canonical form for a nerve net without circles, Bull. Math. Biophys (в печати).
49. Valentinuzzi M., A mathematical interpretation of motor reactions to fixed and moving stimulation of the eye, Bull. Math. Biophys., 21 (1959), 327-341.
50. von Neumann J., Probabilistic logics and the synthesis of reliable organism from unreliable components; Automata studies, Princeton, New York, 1956, стр. 45-98. (Русский перевод; Нейман Дж., Вероятностная логика и синтез надежных организмов из ненадежных компонент, сб. "Автоматы", ИЛ, М., 1956.)
51. White H., The formation of cell assemblies, Bull. Math. Biophys., 23 (1961), 43-53.
52. Wiener N., Cybernetics, New York, 1948. (Русский перевод: Винер Н., Кибернетика, изд. "Сов. радио", М., 1958.)
53. Williams C. M., Representation of locality in a biological information system, Bull. Math. Biophys., 20 (1958), 217-230.
54. Young C, Householder H. S., A note on multi-dimensional psychophysical analysis, Psychometrika, 6 (1941), 331-333.