3.2. Свойство конечной степени

Во второй части этой главы мы обсудим другую довольно трудную проблему, связанную с регулярными языками. Эта проблема оставалась открытой долгое время и была решена лишь в конце 70-х годов нашего века.

Будем говорить, что регулярный язык L обладает свойством конечной степени (сокращенно СКС), если множество {Lⁱ|i = 0, 1, 2, ...} конечно..

Другое понятие, связанное с этим, определяется так: порядком регулярного языка L называется наименьшее целое k, удовлетворяющее условию L^k = L^k+1; если такого k не существует, то будем говорить, что порядок L равен ∞.

Взаимосвязь между только что определенными понятиями устанавливается следующей простой леммой.

Лемма 3.6. Для непустого регулярного языка L являются эквивалентными следующие условия: (i) L обладает СКС; (ii) существует такое целое k, что порядок L равен k; (iii) существует такое целое k, что L^k = L^*.

Доказательство. Прежде всего заметим, что каждое из условий (i) - (iii) влечет принадлежность λ языку L, так как в противном случае при всех целых i кратчайшее слово из Lⁱ было бы короче кратчайшего слова из Lⁱ⁺¹. Поэтому каждое из условий (i)-(iii) влечет также выполнение соотношения Lⁱ⊆Lⁱ⁺¹ при всех i, откуда сразу следует эквивалентность условий (i)-(iii). В частности, отметим, что из условия (ii) вытекает, что L^k = L^k+1 при всех i. □

Приведем несколько простых примеров. Ни один конечный язык L, содержащий непустое слово, не обладает СКС. Значит, такой L является языком бесконечного порядка. Это утверждение является непосредственным следствием того факта, что для любого i слово наибольшей длины из Lⁱ⁺¹ длиннее слова наибольшей длины из Lⁱ.

Любой звездный язык, т. е. регулярный язык вида L^*, обладает СКС. В действительности порядок такого языка равен 1. Менее тривиальными примерами являются язык L₁, заданный регулярным выражением λ∪a²(a³)^*, и язык L₂, заданный регулярным выражением

Оба языка - и L₁, и L₂ - обладают СКС. Читатель при желании может проверить, что порядок языка L₁ равен 3, в то время как порядок L₂ равен 2.

Проблема СКС состоит в нахождении алгоритма, позволяющего по заданному произвольному регулярному языку установить, обладает ли этот язык СКС. В свете теорем 2.8, 2.9 и леммы 3.6 очевидно, что эта проблема эквивалентна проблеме нахождения порядка произвольного регулярного языка L.

Хотя некоторые частные случаи проблемы СКС решаются сравнительно легко (см. упр. 3-5), решение этой проблемы в общем случае оказалось весьма трудным и было завершено сравнительно недавно. Оставшаяся часть настоящей главы посвящена изложению этого решения.

Прежде всего введем понятие, которое даст нам интуитивную основу для последующих рассуждений. (В этом состоит единственная цель вводимого понятия; доказательства можно провести и без него.)

Для каждого конечного детерминированного автомата G итерат G^* автомата G - конечный (вообще говоря, недетермированный) автомат - определяется следующим образом.

Множество вершин G^* состоит из множества вершин G и вершины I (от слова iterate). Множества начальных и заключительных вершин G^*, равно как и алфавит пометок, совпадают с соответствующими объектами в G. (В частности, /Iне является заключительной вершиной.) Все стрелки, имеющиеся в G, есть и в G^*. Кроме того, в G^* имеются стрелки, ведущие в новую вершину I и исходящие из нее. Эти дополнительные стрелки получаются следующим образом. Каждой стрелке G, ведущей из вершины q в заключительную вершину и помеченный буквой a, в автомате G^* соответствует стрелка, ведущая из q в I и помеченная той же буквой a. Каждой стрелке в G, помеченной буквой a и ведущей из начальной вершины в вершину q, в G^* соответствует стрелка, помеченная буквой а и ведущая из I в q; кроме того, если q - заключительная вершина, то в G^* имеется помеченная буквой а стрелка, ведущая из I в I.

Например, если G - конечный детерминированный автомат

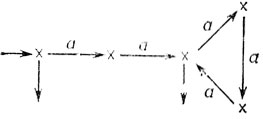
то G^* определяется графом

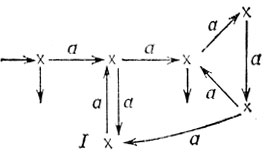
Как и прежде, мы выделяем начальные (соответственно заключительные) вершины малыми входящими (соответственно выходящими) стрелками. Заметим, что автомат G представляет язык L₁, рассмотренный выше и заданный регулярным выражением λ∪a²(a³)^*.

Лемма 3.7. (L(G))^* = L(G^*)∪(λ).

Доказательство. Это равенство непосредственно вытекает из определения G^*. Рассмотрим в (L(G))^* слово w≠λ. Его можно записать в виде

Последовательно перебирая все i<n, можно построить путь в G^* из начальной вершины в I, помеченный x₁, ..., x_i. Приняв x_n за пометку для пути, ведущего из I в заключительную вершину, получим, что до принадлежит L(G^*). С другой стороны, если в G^* существует помеченный словом до путь из начальной вершины в I, то слово до принадлежит (L(G))^*. Этот факт легко устанавливается по индукции. Он показывает также (согласно определению G^*), что каждое слово из L(G^*) принадлежит (L(G))^*. Заметим, что λ не обязательно принадлежит L(G^*), а посему его необходимо присоединить к последнему посредством операции объединения. □

Для заданного слова до в общем случае существует несколько путей в G^*, которые исходят из начальной вершины и помечены словом w. Рассматривая такие пути, обратим внимание на то, сколько раз проходится выделенная вершина I.

Итерационным числом слова w∈L(G^*) (обозначаемым IN (w)) называется наименьшее целое число k, такое, что в G^* существует помеченный словом до путь, ведущий из начальной вершины в заключительную и k раз проходящий через вершину I.

Например, для рассмотренного выше автомата G оказывается, что IN(a⁵) = 0, IN(a⁴) = 1, IN (a⁶) = 2. Можно показать, что в этом случае IN (aⁱ) ≤ 2 для всех i.

Очевидно, что итерационное число слова зависит от автомата G, однако вместо IN_G(w) мы используем более простое обозначение IN (w), поскольку из контекста всегда будет сно, о каком автомате идет речь. То же можно сказать и i некоторых других обозначениях, которые вводятся ниже.

В дальнейшем положим L(G) = R. Таким образом, R^* = L(G^*)∪{λ} Мы предполагаем также, что R содержит непустое слово.

Лемма 3.8. Пусть w - непустое слово в R^* и lN(w) = k. Тогда w принадлежит R^k+1, но не принадлежит никакому Rⁱ, при i<k+1.

Доказательство. По определению G^* слово до можно записать в виде w = x₁ ... x_k+1, где x₁∈R при всех j, 1≤j≤k+1. Стало быть, w ∈ R^k+1.

Предположим, что w можно записать в виде

Так как автомат G представляет язык R, то, согласно (3.17), G^* существует путь из начальной вершины в заключительную, помеченный словом w и проходящий только i-1 раз грез вершину I. Поскольку i-1 <k, последнее утверждение противоречит тому факту, что IN (w) = k. □

Лемма 3.8 показывает также, что для данных R и w∈R^* число IN (w) не зависит от представляющего R автомата.

Мы уже говорили, что в силу недетерминированности автомата G^* слову до может соответствовать несколько помеченных этим словом путей, выходящих из начальной вершины G^*. Более того, эти пути не обязательно заканчиваются в одной и той же вершине. Исходя из этого, определим START(w) как множество всех таких вершин q≠I в G^*, что в G^* существует помеченный словом до путь из начальной вершины в q.

Таким образом, START(w) является множеством возможных конечных точек путей, помеченных словом w. Заметим, что мы требуем, чтобы эти пути оканчивались в "собственно автомате G^* в силу условия q≠I. Множество START(w) определяется для любого слова w (а не только для слов из R^*).

Аналогично END (w) определяется как множество всех таких вершин q≠I в G^*, что в G^* существует помеченный до путь из q в одну из заключительных вершин.

Чтобы лучше уяснить понятие START (w), заметим, что его можно определить, не обращаясь к итерату G^* (если нам заданы только G и L(G) = R). Это делается следующим образом. START(w) есть множество таких вершин q в G, что для некоторого разложения w = w₁w₂, где слово w₁ принадлежит R^*, существует помеченный словом w₂ путь из начальной вершины G в вершину q. Аналогично END (w) можно определить как множество таких вершин q в G, что либо существует помеченный до путь из q в заключительную вершину, либо для некоторого разложения w = xyz выполняются следующие условия: (i) существует помеченный словом x путь из q в заключительную вершину; (ii) y принадлежит R^*; (iii) существует помеченный словом z путь из начальной вершины в заключительную (т. е. z∈R). Заметим, что START (λ) состоит из всех начальных вершин, а END (λ) - из всех заключительных вершин.

Непосредственным следствием леммы 3.7 и определений START (w) и END (w) является следующий результат.

Лемма 3.9. Пусть непустое слово w из R^* можно представить в виде w = w₁w₂. Тогда множество

непусто. Обратно, если для слова w = w₁w₂ множество (3.18) непусто, то слово w принадлежит R^*.

До сих пор рассмотренные понятия и леммы не относились непосредственно к СКС. Следующая лемма прямо связана с СКС и играет важную роль в последующем обсуждении.

Лемма 3.10. Пусть w = xyz - непустое слово в R^*, такое что

Тогда если R обладает СКС, то в множестве

существуют вершины q и q' (не исключено, что q = q'), для которых в G имеется помеченный словом у путь из q в q',

Доказательство. Прежде всего заметим, что в силу (3.19) и леммы 3.9 пересечение (3.20) непусто.

Доказательство проведем от противного, предполагая, что если q и q' принадлежат (3.20), то не существует пути из q в q', помеченного словом y. (Напомним, что путь, не содержащий стрелок, считается помеченным λ.) Из (3.19) следует, что для всех i и j

В силу леммы 3.9 отсюда вытекает, что для любого i слово xyⁱz принадлежит R^*. С другой стороны, согласно нашему предположению, для всех i

(Для того чтобы доказать это неравенство, рассмотрим помеченный словом x путь p из начальной вершины в вершину, лежащую в (3.20). Чтобы продолжить p путем, помеченным y и оканчивающимся в вершине из (3.20), необходимо пройти через I. Это относится к каждому пути, помеченному y, что и дает (3.21).)

Но теперь, согласно (3.21) и лемме 3.8, для любого k можно найти слово до из R^*, не принадлежащее R^k. Это противоречит тому факту, что R обладает СКС.□

Лемма 3.10 имеет следующий интуитивный смысл. Если R обладает СКС, то мы хотим доказать, что существует число k, вычисляемое только по автомату G и такое, что R^k = R^*. Для этого надо установить, что каждое слово до из R^* принадлежит R^k. Записывая до в виде w = xyz, так что выполняется (3.19), мы ищем такое число i ≤ k, что w∈Rⁱ. Теперь из леммы 3.10 вытекает, что подслово y увеличивает искомый показатель i самое большее на единицу, так как помеченный y путь лежит в G и, следовательно, не проходит через I.

Проведем теперь это рассуждение более подробно. Для этого нам потребуются некоторые новые понятия и обозначения.

Число элементов конечного множества S будем обозначать через #S.

Определим порядок слова w из R^* как

Кроме того, для каждого слова w из R^* определим

WORST (w) = (i, j), где

Таким образом PAIRS (w) содержит все возможные пары множеств вершин, полученных различными разложениями слова w. Первая комионента WORST(w) равна максимальному числу i, получаемому суммированием мощностей двух множеств в элементах PAIRS (w), а вторая компонента равна числу j способов, которыми достигается этот максимум.

Если w≠λ, то (согласно лемме 3.9) оба множества в каждом элементе PAIRS (w) непусты. Итак, i≥2. Обозначая общее число вершин G через n, получаем оценки

Кроме того 1≤j≤(²ⁿ_i).

Обозначая через b_n наибольший биномиальный коэффициент (²ⁿ_i), где 2≤i≤n, получаем

Заметим, что оценку j≤(²ⁿ_i) можно было бы слегка улучшить, принимая во внимание тот факт, что оба множества в каждом элементе множества PAIRS (w) непусты. Однако мы стремимся получить не наилучшие, а наиболее простые оценки. Это замечание относится и к другим частям настоящего доказательства.

Теперь рассмотрим пару (i, j), такую, что выполняются условия (3.22) и (3.23). На множестве таких пар вводится лексикографическое упорядочение: (i₁, j₁)≤(i₂, j₂), если либо i₁<i₂, либо i₁ = i₂ и j₁≤j₂.

Пусть i и j удовлетворяют (3.22) и (3.23), а R обладает СКС; введем следующие обозначения:

Мы предположили, что R обладает СКС, потому что в противном случае максимум может не существовать. Будем считать, что o(i, j) = 1, если в R^* нет такого слова да, что WORST (w)≤(i, j). Аналогично o(i) = 1. если в R^* нет такого да, что WORST (w) ≤(i, b_n), т. е. в R^* нет такого да, что первая компонента WORST (w) не превышает I. Указанные соглашения гарантируют, что o(i, j) и 0(i) определены для всех i и j, удовлетворяющих (3.22) и (3.23).

Непосредственно из определения следует, что при (i₁, j₁)≤(i₂, j₂) имеет место o(i₁, j₁)≤o(i₂, j₂). Этим свойством монотонности обладает также и одноместный оператор o: из i₁≤i₂ следует, что o(i₁)≤o(i₂). Более того, если R обладает СКС, то o(w)≤o(2n) для всех слов да из R^*.

Нам надо доказать, что существует число c_n, эффективно вычисляемое по числу n вершин автомата G и такое, что

при условии, что R обладает СКС. Это позволит нам выяснять, обладает ли данное R СКС или нет: мы строим G и проверяем, выполняется ли равенство R^c_n = R^*.

Самым существенным инструментом в доказательстве (3.24) является следующая лемма.

Лемма 3.11. Пусть R обладает СКС, и пусть для чисел i≥3, j≥2 выполняются условия (3.22) и (3.23). Тогда

Доказательство. Если в R^* нет такого слова w, что WORST (w) = (i, j), то o(i, j) = o(i, j-1). Следовательно, имеет место (3.25). Таким образом, для доказательства леммы нам нужно только установить, что для любого слова w с WORST (w) = (i, j) выполняется неравенство

(Отметим, что при этом учитывается также тот случай, когда порядок каждого слова w, для которого WORST (w) = (i, j), в действительности не превосходит o(i, j-1).) Рассмотрим произвольное, но фиксированное w, для которого WORST (w) = (i, j). Можно предположить, что w≠λ, поскольку o(λ) = 0. (В действительности (3.26), конечно, выполняется при |w|≤5.)

Запишем теперь w в виде w = xz₁, где

и, кроме того, x - кратчайший префикс слова w, обладающего этим свойством. (Иначе говоря, из равенств w = x'z₁ и

следует, что |x|≤|x'|.) Введем обозначения

и запишем z₁ в виде z₁ = yz, где

и, кроме того, z - кратчайший суффикс слова z₁, обладающего этим свойством. (Иначе говоря, из равенств z₁ = y'z' и

следует, что |z|≤|z'|.)

Таким образом, w = xyz. Возможно, что одно или два из слов x, y, z равны λ.

По лемме 3.10 в S∩S' можно найти такие вершины q и q', что в G имеется путь из q в q', помеченный словом y. Продлим теперь этот путь до пути из начальной вершины в конечную следующим образом.

Пусть u - такой суффикс слова x, что в G существует путь из начальной вершины в вершину q, помеченный словом u. Аналогично пусть v - такой префикс слова z, что в G существует путь из q' в заключительную вершину, помеченный словом v. (Конкретнее, в качестве путей, помеченных словами u и v, мы берем подпути пути, помеченного словом w = xyz.) Таким образом, x = w₁u, z = vw₂ и w = w₁uyvw₂ для некоторых слов w₁ и w₂ из R^*. Существование u и v обеспечивается тем, что w принадлежит R^*. Кроме того, слово uyv принадлежит R. Возможно, что одно из слов u и v или оба они пусты.

Из того, что uyv∈R, и из очевидного для всех слов w', w" неравенства o(w'w")≤o(w') + o(w") получаем

Если u≠λ, то выбор слова x гарантирует, что o(w₁)≤o(i-1). (Очевидно, что если разложение w_i приводит к максимальному числу i, то это i может быть достигнуто в w до вхождения в x.) Если u = λ, а w₁≠λ, то запишем w₁ (=x) в виде w₁ = w₃w₄, где w₃∈R^*, а w₄≠λ принадлежит R. Отсюда ясно, что

Так как (3.28), очевидно, выполняется и для w₁ = λ, мы заключаем, что (3.28) имеет место во всех случаях.

Если v≠λ, то выбор слова z гарантирует, что o(w₂)≤o(i, j-1). (Действительно, все максимальные пары с общим числом элементов i, которые могут быть получены из разложений w₂, могут быть получены и из разложений w, но при этом пара (S, S') не может быть получена из разложения w₂.) Если v = λ, а w₂≠λ, то запишем w₂ (=z) в виде w₂ = w₅w₆, где w₆∈R^*, а w₅≠λ принадлежит R. Это показывает, что

Ясно, что это неравенство выполняется и при w₂ = λ, так что оно имеет место во всех случаях.

Теперь (3.26) оказывается непосредственным следствием (3.27) - (3.29), откуда и вытекает утверждение леммы.

Лемма 3.12. Пусть R обладает СКС, а число i≥3 удовлетворяет соотношению (3.22). Тогда o(i, 1)≤2o(i-1) + 3.

Доказательство проводится в точности так же, как доказательство предыдущей леммы, однако в данном случае в качестве верхней границы при рассмотрении w₂ фигурирует o(i-1) вместо о (i,j-1).

Напомним, что мы стремимся получить верхнюю оценку для о (2я). Предыдущие леммы сводят получение этой оценки к нахождению оценок для меньших значений I. Нам остается получить оценку для "конечной ситуации".

Лемма 3.13. Если R обладает СКС, то o(2)≤1.

Доказательство. Если в R^* нет таких слов w, что первая компонента WORST(w) равна 2, то равенство o(2) = 1 следует из определения o(2).

Рассмотрим произвольное w≠λ из R^*, такое, что первая компонента WORST(w) равна 2. В силу леммы 3.9 из этого условия следует, что для любого разложения w = w₁w₂ множество START(w₁) = END (w₂) состоит в точности из одной вершины. Следовательно, любому пути р в G^*, помеченному словом w, исходящему из начальной вершины и один или несколько раз проходящему через вершину I, соответствует путь в G, помеченный словом w, исходящий из начальной вершины и оканчивающийся в той же вершине, что и p. Это означает, что w∈R и, следовательно, o(λ) = 1. Так как o(λ) = 0, то лемма доказана.

В лемме 3.13 предположение о том, что R обладает СКС, было сделано только потому, что это предполагалось в определении o(i). В противном случае (т. е. при обобщении определения o(i)) доказательство леммы 3.13 не опиралось бы на это предположение. Теперь мы готовы установить основной результат.

Теорема 3.14. Пусть R - регулярный язык, который может быть представлен конечным детерминированным автоматом с n вершинами. Тогда существует натуральное число c_n, эффективно вычисляемое по n и такое, что R обладает СКС тогда и только тогда, когда

Следовательно, проблема СКС разрешима. Более того, существует алгоритм для нахождения порядка данного регулярного языка.

Доказательство. Пусть язык R обладает СКС. Последовательное применение леммы 3.11 прежде всего дает для каждого i, такого, что 3≤i≤2n, соотношения

Применяя лемму 3.12, отсюда получаем

Теперь положим a_n = 4(b_n+1) и c_n = a_n^2n-2. Тогда для 3≤i≤2n выполняется неравенство o(i)≤a_no(i-1). Следовательно,

Отсюда по лемме 3.13

Так как порядок каждого слова w из R^* не превосходит o(2n), то (3.30) непосредственно следует из (3.31).

Мы показали, что если R обладает СКС, то имеет место (3.30). Очевидно, что если R не обладает СКС, то (3.30) не выполняется. Значит, проблему СКС можно решать следующим образом. Для данного R (с помощью G) сначала вычислим c_n, а затем проверим, выполняется ли (3.30). Эту проверку можно осуществить в силу теоремы 2.8.

Порядок данного регулярного выражения R можно теперь найти следующим образом. Сначала указанным выше способом выясним, обладает ли R СКС. Если R не обладает СКС, то по лемме 3.6 порядок R бесконечен. В противном случае проверяем для k = 0, 1, 2 ..., верно ли, что

Эта последовательность проверок обрывается, так как R обладает СКС. Порядок R равен наименьшему k, при котором выполнено (3.32).▫

Мы закончим настоящую главу другой интересной характеризацией СКС. Эта характеризация (существование слова с особым свойством) может, в частности, проверяться способом, не использующим приведенные выше результаты. Подробности можно найти в [Lil].

Теорема 3.15. Порядок непустого регулярного языка R бесконечен тогда и только тогда, когда в R^* существует такое слово w, что wⁱ∉Rⁱ для всех i≥1.

Доказательство. Часть "тогда" утверждения теоремы очевидна. (В самом деле, если w∈R^*, то и wⁱ∈R^* при всех i.) Чтобы доказать часть "только тогда", предположим, что порядок R бесконечен. Тогда в R^* существует такое слово xyz, что

и, кроме того, для любых вершин q и q' из множества

в конечном детерминированном автомате G, представляющем R, не существует пути из q в q', помеченного y. Это доказывается следующим образом. Единственное следствие из СКС, используемое в доказательстве леммы 3.11 и в дальнейших рассуждениях, приводящих к оценке o(2n)≤c_n,- это заключение леммы 3.10. Следовательно, обращение леммы 3.10 также верно: если R не обладает СКС, то в R^* существует такое слово xyz, что (3.19) выполняется, но утверждение о множестве (3.20) не выполняется.

Как и в доказательстве леммы 3.10, мы заключаем теперь, что для всех i слово xyⁱz принадлежит R^* и

Кроме того, для любого q из S существует путь в G^* (но не в G) из q в некоторую вершину из S, помеченный словом у. Из конечности множества S следует, что найдутся вершина q из S, декомпозиция y = y₁y₂ и целое число m, такие, что в G^* существует путь из q в заключительную вершину (соответственно из начальной вершины в q), помеченный y₁ (соответственно y₂y^m). Следовательно, y₂y^my₁ = (y₂y₁)^m+1∈R^*.

Теперь введем обозначение t = 2|xyz| и определим w как w = (y²y^my₁)^t. Слово w принадлежит R^*, потому что y²y^my₁ принадлежит R^*.

Чтобы убедиться в том, что w удовлетворяет поставленному условию, предположим противное: для некоторого i≥1 слово wⁱ принадлежит Rⁱ. Тогда слово

принадлежит R^i+|zyx|. Но этот результат противоречит (3.33) и лемме 3.8, так как

В заключение заметим, что оценка c_n, полученная в теореме 3.14, может оказаться сильно завышенной в свете того факта, что не известен ни один пример регулярного языка, имеющего порядок больше n (число вершин представляющего автомата), который при этом обладал бы СКС.