3. Регулярность; интересные проблемы

3.1. Звездная высота

Простейшие средства задания языков - регулярные выражения (или конечные автоматы) и DOL-системы - явились источником математически интересных и захватывающих задач. Многие, в том числе и автор этой книги, предпочитают задачи, которые можно без труда объяснить даже полному профану в соответствующей области, таким задачам, в которых основная трудность заключается в том, чтобы разобраться во введенных понятиях. Типичным примером задачи первого типа является гипотеза Ферма. По очевидным соображениям мы не станем приводить примеры задач второго типа.

Регулярные выражения и DOL-системы породили много проблем, относящихся к первому из указанных выше классов. Действительно, несмотря на многочисленные попытки решения этих проблем, многие из них до сих пор остаются открытыми.

В этой главе мы приведем решения двух задач, связанных с регулярными языками. Обе они достаточно трудны, так что читатели, самостоятельно нашедшие решение, могут себя поздравить. Обе задачи связаны с операцией звезды - кате-нативного замыкания. Операция звезды лежит в основе рассматриваемой теории, поскольку объединение и катенация позволяют порождать только конечные языки. Однако комбинация звезды с объединением и катенацией приводит к некоторым трудным вопросам.

Мы начнем с введения понятия звездной высоты. По существу звездная высота регулярного выражения есть наибольшее число вложений звезды в выражении, т. е. длина самой длинной цепи вложений звезды в звезду. Звездная высота регулярного языка L представляет собой звездную высоты "наиболее экономного" регулярного выражения а для L, т. е. ни одно из регулярных выражений, задающих L, не имеет звездную высоту меньше α.

Определение.Звездной высотой регулярного выражения α над алфавитом ∑ (обозначается sh(α)) называется неотрицательное целое число, рекурсивно определяемое следующим образом:

(i) буквы из ∑ и ∅ имеют звездную высоту 0;

(ii) если sh(α) = i, а sh(β) = j, то

sh ((α∪β)) = sh ((αβ)) = max (i, j);

(iii) если sh(α) = i, то sh(α^*) = i+1.

Звездная высота регулярного языка L (обозначается sh(L)) есть наименьшее целое i, такое, что sh(α) = i для некоторого регулярного выражения α, задающего L. □

Звездная высота показывает "циклическую сложность" регулярного выражения: выражение с меньшей звездной высотой менее сложно, хотя оно может содержать большее число символов. Можно ли понизить звездную высоту каждого регулярного выражения (настолько, что она не будет превышать определенного предела), выбирая другое регулярное выражение, задающее тот же язык? Иначе говоря, не окажется ли звездная высота любого регулярного языка над ∑ всегда меньше некоторой константы, возможно зависящей от числа букв в ∑? Это первая проблема, которую мы собираемся исследовать в этой главе.

Очевидно, что во многих случаях звездную высоту данного регулярного выражения действительно можно понизить. Для каждого регулярного выражения а выражения α* и (α*)* задают один и тот же язык. Менее тривиальными примерами оказываются две пары регулярных выражений

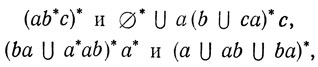
упомянутых в конце гл. 2. В обоих случаях возможно понижение звездной высоты с 2 до 1. Очевидно, что дальнейшее понижение невозможно, поскольку ни один бесконечный язык не имеет звездную высоту, равную нулю.

Пример класса регулярных выражений, звездная высота которых может быть уменьшена радикальным образом, дает следующая теорема.

Теорема 3.1. Каждый регулярный язык над однобуквенным алфавитом ∑ = {a} имеет звездную высоту, не большую 1.

Доказательство. В силу теорем 2.9 и 2.4 можно считать, что L = L(G), где G - конечный детерминированный автомат с алфавитом пометок, равным {a}. Но при этом всегда можно считать, что автомат G имеет вид

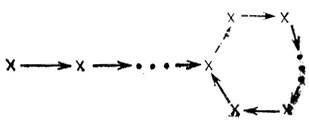
Это означает, что множество целых чисел {i|aⁱ∈L}, упорядоченное по возрастанию, является заключительно периодическим^*. Если соответствующий период равен p, то

где F₁ и F₂ - конечные языки над {a}. Правая часть (3.1), рассматриваемая как регулярное выражение, имеет звездную высоту, равную 1. Следовательно, звездная высота L не превосходит 1. □

^* (Множество натуральных чисел А называется заключительно периодическим (с периодом p), если для некоторого с

x≥c→(x∈A ↔ x+p ∈ A).- Прим. перев.)

В основе теоремы 3.1 лежит следующая интуитивная идея: в случае однобуквенного алфавита имеет значение лишь длина слова, и, следовательно, нет необходимости во вложениях звезды. Это заключение не распространяется на случаи, когда алфавит содержит две или более буквы. Итак, мы хотим установить следующий результат.

Теорема 3.2. Над любым алфавитом, содержащим хотя бы две буквы, существуют регулярные языки с любой звездной высотой.

Для доказательства теоремы 3.2 достаточно показать, что некоторый язык L_i, заданный регулярным выражением α_i со звездной высотой i, нельзя задать никаким регулярным выражением со звездной высотой, меньшей L Определим регулярные выражения α_i для всех значений i≥1.

Сначала заметим, что нам всего лишь нужно показать, что над алфавитом {a, b} существуют регулярные выражения с произвольно заданной звездной высотой ≥1. Это следует, во-первых, из того, что каждое регулярное выражение над {a, b) остается регулярным выражением над любым алфавитом, содержащим {a, b}, и, во-вторых, из того, что, скажем, {a} является регулярным языком со звездной высотой, равной нулю.

Регулярные выражения α_i, i = 1, 2, ..., рекурсивно определяются следующим образом:

Так, например,

Далее, пусть L_i - регулярный язык, заданный регулярным выражением α_i, i = 1, 2, ... . Для завершения доказательства теоремы 3.2 достаточно проверить, что для каждого i звездная высота языка L_i равна i. Поскольку очевидно, что звездная высота α_i равна i для всех i, то sh(L_i)≤i. Следовательно, достаточно показать, что

В доказательстве (3.2) будут использованы слова w(i, j) с i, j ≥1 над алфавитом {a, b}. Эти слова рекурсивно определяются следующим образом:

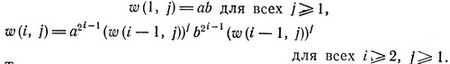
Так, например,

Для каждого слова w над алфавитом (a, b) обозначим через 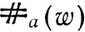число вхождений буквы а в слово w. Подобным же образом определяется 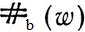. Так,

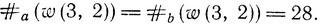
Рассмотрим теперь фиксированное значение i≥1 и обозначим через K_i семейство регулярных языков L над {a, b}, удовлетворяющих следующим трем условиям:

(i) существует такое натуральное t, что для каждого слова w из L имеет место равенство

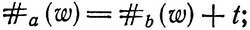
(ii) для бесконечного множества значений j слово (w(i,j))^j входит в качестве подслова хотя бы в одно слово из L;

(iii) из всех языков, удовлетворяющих (i) и (ii), L имеет минимальную звездную высоту, т. е. не существует'регулярного языка L', удовлетворяющего условиям (i) и (ii) и неравенству sh (L')<sh (L).

Сначала сделаем несколько предварительных замечаний относительно семейств K_i. Ясно, что для каждого i язык L_i удовлетворяет условиям (i) (при t = 0) и (ii). (По сути дела тот факт, что язык L_i удовлетворяет условию (ii), доказывается простой индукцией по i: для i = 1 это утверждение очевидно, а шаг индукции совершается согласно определению α_i и w(i,j).) Это показывает, что семейство K_i непусто при всех i≥1. Кроме того, условие (iii) гарантирует, что все языки семейства K_i имеют одну и ту же звездную высоту d_i. Поскольку sh(L_i)≤i и L_i удовлетворяет условиям (i) и (ii), мы заключаем, что

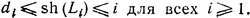
(3.3)

Ясно, что каждый язык, удовлетворяющий условию (ii), должен быть бесконечным. Отсюда вытекает, что d_i не может быть равной нулю, и, следовательно, в силу (3.3)

Рассмотрим теперь произвольное фиксированное i≥2 и произвольный язык L и K_i. Поскольку sh(L) = d_i, мы заключаем, что L является конечным объединением языков, каждый из которых задан регулярным выражением вида

(3.4)

где звездная высота каждого регулярного выражения γ_j (j = 0, ..., 2n) не превосходит d_i-1. (Заметим, что γ₀ или γ_2n может оказаться регулярным выражением ∅.) Кроме того, язык, заданный выражением β, удовлетворяет условию (i), поскольку сам язык L удовлетворяет условию (i). Можно также считать, что язык, заданный выражением |3 (3.5), удовлетворяет условию (ii). (Это следует из того, что L удовлетворяет условию (ii), и поэтому хотя бы один язык из задающего L объединения должен удовлетворять условию

Для доказательства теоремы 3.2 предварительно докажем три леммы.

Лемма 3.3. Ни один из языков, заданных регулярными выражениями γ_u, u = 0, ..., 2n, в (3.5), не удовлетворяет условию (ii).

Доказательство. Предположим противное: пусть для некоторого и язык L', заданный выражением γ_u, удовлетворяет условию (ii). Тогда V удовлетворяет также условию (i), так как язык, заданный выражением β, удовлетворяет (i), и, согласно определению β, существуют такие слова w₁ и w₂, что слово w₁ww₂ принадлежит языку, заданному выражением β, коль скоро w принадлежит L'.

Но из того, что L' удовлетворяет условиям (i) и (ii) и имеет меньшую звездную высоту, чем L, следует, что L не удовлетворяет условию (iii). Это противоречие доказывает лемму 3.3. □

Лемма 3.4. Существует такое натуральное u, 0≤u≤n, что язык, заданный выражением γ_2u в (3.5), удовлетворяет условию (ii).

Доказательство. Предположим противное. Тогда, согласно лемме 3.3, ни один из языков, заданных регулярными выражениями

(3.6)

не удовлетворяет условию (ii). Из конечности множества этих языков следует, что существует такое целое j₀, что при всех j>j₀ слово (w(i,j))^j не входит в качестве подслова ни в одно слово, принадлежащее какому-либо из языков, заданных регулярными выражениями (3.6).

В силу теоремы 2.9 язык, заданный регулярным выражением β, может быть представлен конечным детерминированным автоматом G. Обозначим число вершин в G через j₁. Так как язык L_β, заданный регулярным выражением β, удовлетворяет условию (ii), существует натуральное число

такое, что (w(i, j₂))^j₂ является подсловом некоторого слова в L_β. Следовательно, существуют такие слова w₁ и w₂, что слово w₁(w(i, j₂))^j₂w₂ принадлежит L_β. Согласно (3.7), j₂ превосходит число вершин автомата G. Отсюда следует, что существуют такие целые числа m₁ и m₂, 1≤m₁<m₂≤j₂, что слова w₁(w(i, j₂))^m₁ и w₁(w(i, j₂))^m₂ переводят автомат G из начальной вершины в одну и ту же вершину. Полагая m = m₂ - m₁, заключаем, что слова

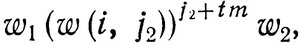(3.8)

где t - произвольное неотрицательное целое число, принадлежат L_β.

Вспоминая определения j₀ и L_β, заключаем, что ни одно из слов (w(i, j₂))^j, где j>(2n + 1)j₂, не является подсловом никакого слова из L_β. (В противном случае слово (w(i, j₂))^j₂ было бы подсловом какого-либо слова в одном из языков, заданных регулярными выражениями (3.6).) Но это заключение противоречит тому факту, что все слова (3.8) принадлежат L_β. □

Лемма 3.5. Существует целое число u, 0≤u≤n, такое, что язык L^(2u), заданный выражением γ_2u в (3.5), удовлетворяет следующему условию (модификации условия (ii)): для бесконечного множества значений j слово (w(i-1, j))^j входит в качестве подслова хотя бы в одно из слов языка L^(2u).

Доказательство. Мы утверждаем, что целое число и из леммы 3.4 удовлетворяет также лемме 3.5. Снова предположим противное: существует такое натуральное j₀, что для всех j>j₀ слово (w(i-1, j))^j не входит в качестве подслова ни в одно слово из L^(2u).

Согласно лемме 3.4, язык (L^(2u))^* удовлетворяет условию (ii). Следовательно, существует такое целое число j₁>j₀, что слово

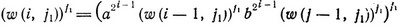
является подсловом некоторого слова из (L^(2u))^*. Значит, и слово w(i, j₁) есть подслово некоторого слова из (L^(2u))^*. Поэтому существует целое число v и слова w₁, ..., w_v из L^(2u), такие, что

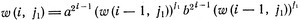(3.9)

слова w₁, ..., w_v.

Как было показано выше (см. доказательство леммы 3.3), язык L^(2u) удовлетворяет условию (i). Но язык (L^(2u))^* также удовлетворяет условию (i), поскольку язык Lp, заданный выражением (3, удовлетворяет (i). Более того, язык L_β должен удовлетворять условию (i) при t = 0, поскольку язык (L^(2u))^* содержит пустое слово. Отсюда следует, что и язык L^(2u) удовлетворяет условию (i) при t = 0.

Следовательно, в каждом из слов

число вхождений a равно числу вхождений b. Напомним, что (3.9) является подсловом в слове w₁, ..., w_v. Выясним теперь, почему это возможно.

Обозначим через p, 1≤p≤v, такое целое число, что первое вхождение слова

в (3.9) начинается внутри w_p (когда мы рассматриваем некоторое фиксированное вхождение (3.9) как подслово в слове w₁, ..., w_v), а через q такое целое число, что первое вхождение (3.11) в (3.9) оканчивается внутри w_q. Тогда q>p, поскольку из равенства q = p следовало бы, что слово (3.11) входило бы в качестве подслова в w_p, а это невозможно по определению j₀ и выбору j₁. Значит, можно записать, что

где x - собственный суффикс слова (3.11).

Из определения слов w(i,j) вытекает, что (1) ни один суффикс слова (3.11) не содержит больше букв a, чем букв b, и (2) каждый префикс слова

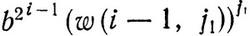(3.13)

(включая само это слово) содержит больше букв b, чем букв a.

Так как w_q содержит одинаковое число букв a и b, то из условий (1) и (2) следует, что y в (3.12) должно быть пустым словом λ. Следовательно, слово (3.13) является префиксом слова w_q+1, ..., w_v. Но в силу условия (2) такой факт может иметь место только тогда, когда (3.13) является префиксом слова w_q+1. Так как j₁>j₀, это опять-таки противоречит выбору j₀, и полученное противоречие доказывает лемму 3.5.

Теперь мы в состоянии доказать (3.2), а тем самым и теорему 3.2.

Согласно лемме 3.5, язык L^(2u) удовлетворяет условиям (i) и (ii)' (последнее получается из (ii) заменой i на i-1). Это влечет неравенство

С другой стороны, мы видели, что язык, заданный одним из регулярных выражений γ в (3.5), имеет звездную высоту не более d_i-1. Поэтому имеет место следующее неравенство:

Так как i≥2 было выбрано произвольно, из (3.14) и (3.15) следует, что

Неравенство (3.2) непосредственно получается из (3.3), (3.4) и (3.16).□

Хотя теорема 3.2 дает решение одной из основных проблем, связанных со звездной высотой (проблемы построения языков с произвольно выбранной звездной высотой), многие другие важные проблемы, касающиеся звездной высоты, все еще остаются открытыми. Наиболее известной из них является так называемая проблема звездной высоты, состоящая в нахождении алгоритма для определения звездной высоты произвольного регулярного языка. Хотя установлен ряд результатов в духе теоремы 2.8, ни одна из многочисленных попыток решить указанную проблему до сих пор не завершилась успехом. Родственные вопросы обсуждаются в упр. 1.