4. Коды и множества совпадения

4.1. Основные свойства кодов

В настоящей главе перед нами стоят две задачи. Во-первых, мы хотим совершить краткий экскурс в теорию кодов. Эта теория дала ряд красивых результатов, применимых к различным разделам теории языков. Во-вторых, мы хотим обсудить некоторые недавно введенные понятия, тесно связанные с теорией кодов. Эти понятия нам потребуются в гл. 5 и 6. Подчеркнем, что мы не будем обсуждать так называемые коды с исправлением ошибок, а будем иметь дело исключительно с алгебраической теорией кодов, обычно рассматриваемой как часть теории полугрупп¹.

¹ (Более глубоко и детально ознакомиться с различными вопросами алфавитного кодирования и смежными проблемами теории конечных автоматов читатель может по работам [Л1^*], [Л2^*], [Мар2^*].- Прим. перев.)

На интуитивном уровне код¹ можно определить как такое множество слов, что любое произведение этих слов может быть "декодировано" только одним способом. Рассмотрим, например, множество слов

¹ (В отечественной литературе в этом смысле часто употребляется термин "кодовое множество".- Прим. перев. )

Можно закодировать этими словами символы 0, 1, 2, 3 и "морфически" распространить это кодирование на все слова в алфавите {0,1,2,3}. Так, кодом слова 012230 будет слово

Гарантией однозначности декодирования служит тот факт, что каждое слово в алфавите {a, b} может быть представлено в виде произведения слов (4.1) не более чем одним способом. Этот факт легко установить, читая слова в алфавите {a, b) справа налево: каждое закодированное слово должно кончаться на одно из слов (4.1). Таким способом символы 0, 1, 2, 3 можно получить один за другим с правого конца. Это означает, что (4.1) является кодом.

С другой стороны, множество {a, ab, ba) не является кодом. Например, слово aba декодируется двумя разными способами: aba =(ab)a = a(ba).

Определение. Непустой язык C в алфавите ∑ называется кодом, если для любых слов x_i1, x_i2, ..., x_im, x_j1, ..., x_jn из C, таких, что

имеет место x_i1 = x_j1. ▫

Если C является кодом, то из (4.2), очевидно, следует, что m = n и x_it = x_jt при t = 1, ..., m. Таким образом, каждое слово в C^* единственным образом декодируется как произведение слов из C. Очевидно также, что в код не может входить пустое слово и что непустое подмножество кода также является кодом. Будем считать, что алфавит ∑ содержит не менее двух символов, так как однобуквенный алфавит тривиален с точки зрения кодирования. Теперь установим два довольно простых характеристических свойства кодов.

Лемма 4.1. Непустой язык C над алфавитом ∑ является кодом тогда и только тогда, когда существует множество символов ∑₁ и биекция ∑₁ на C, которую можно продолжить до инъективного морфизма ∑₁^* в ∑^*.

Доказательство. Прежде всего заметим, что множество символов ∑₁ может быть бесконечным (тем не менее понятно, что означает при этом ∑₁^*).

Рассмотрим часть "тогда" утверждения леммы. Предположим, что существуют ∑₁ и биекция φ: ∑₁→C, удовлетворяющие условию продолжения. Чтобы доказать, что C представляет собой код, рассмотрим произвольные слова x_i1, ..., x_im, x_j1 ..., x_jn из C, удовлетворяющие (4.2). Обозначая φ^-1 (x_it) = a_it (соответственно φ^-1 (x_jt) = a_jt получаем

(Здесь φ уже продолжено на ∑₁^*.) Тот факт, что отображение φ инъективно, влечет равенство

Следовательно, a_i1 = a_j1, откуда x_i1 = φ(a_i1) = φ(a_j1) = x_j1, и значит, С является кодом.

Рассмотрим часть "только тогда". Предположим, что C есть код. Пусть ∑₁ - множество символов той же мощности, что C, а φ: ∑₁→C - биекция, где соответствующие элементы обозначены одинаковыми нижними индексами. Это отображение естественным образом продолжается до морфизма ∑₁^* в ∑^*. Нам еще надо доказать, что это продолжение φ инъективно.

Допустим противное: существуют элементы ∑₁, удовлетворяющие условиям

Без потери общности можно предположить, что m в (4.3) является наименьшим из возможных: (4.3) не выполняется ни для какого m₁<m. Следовательно, a_i1 ≠ a_j1. (При a_i1 = a_j1 мы получили бы

что противоречит минимальности m.) Таким образом, мы имеем

и a_i1 ≠a_j1. Так как ф есть биекция, то последнее неравенство влечет x_i1 ≠ x_j1, а это с учетом (4.4) противоречит предположению, что C является кодом. Отсюда следует инъективность продолжения отображения φ. ▫

Следующий результат известен под названием критерия Шютценберже. Будем говорить, что язык L катенативно-независим, если никакое слово w из L нельзя представить как произведение

Лемма 4.2. Катенативно-независимый непустой язык C над ∑ является кодом тогда и только тогда, когда для любого слова w в алфавите ∑ из того, что оба языка C^*w и wC^* пересекаются с C^*, следует, что w принадлежит C^*.

Доказательство. Сначала рассмотрим часть "тогда" утверждения леммы. Предположив, что C удовлетворяет условию леммы, мы должны показать, что C является кодом. Допустим противное: в C существуют такие слова x_v, что

Согласно (4.5), одно из слов x_i1 и x_j1 является префиксом другого. Без потери общности можно считать, что

Согласно (4.5) и (4.6), языки C^*y и C^* (соответственно yC^* и C^*) пересекаются, имея общий элемент x_j1 (соответственно x_i2 ... x_im). (Заметим, что из (4.5) и (4.6) следует, что m≥2.) Поскольку С удовлетворяет условию о пересечениях, получаем, что y принадлежит C^*. Однако в силу (4.6) это заключение противоречит допущению о катенативной независимости языка.

Теперь рассмотрим часть "только тогда". Предположим, что С является кодом, и докажем от противного, что выполняется условие о пересечениях. Итак, предположим, что это условие не выполнено, т. е. что в C найдутся элементы x_v, а в C^* - элементы y_v и такое слово w∉C^*, что

Снова предполагая минимальность m, заключаем, что x_i1 ≠ x_j1 (В противном случае мы получили бы равенство вида (4.7) с меньшим m.) Теперь мы получаем, что

это противоречит предположению о том, что C есть код. ▫

Условие леммы 4.2 можно сформулировать более компактно: для каждого слова w из ∑^*

Очевидно, что если все три множества C^*w, wC^* и C^* имеют общий элемент, то пересекаются и пары множеств C^*w, C^* и wC^*, C^*. Обратно, если wx₁ = x₂ и x₃w = x₄, где x₁, x₂, x₃, x₄∈C^*, то wx₁x₄ = x₂x₄ = x₂x₃w, откуда следует, что пересекаются все три множества. Заметим, однако, что одно лишь условие (4.8) (без допущения о катенативной независимости множества C) не гарантирует еще, что C является кодом.

Леммы 4.1 и 4.2 сами по себе не дают нам эффективного метода, позволяющего определить, является ли данный язык кодом, однако такие алгоритмы (для конечных языков) существуют. В сущности результаты гл. 2 приводят к следующему алгоритму: надо проверить, пусто ли множество x₁C^*∩x₂C^* для каждой пары (x₁, x₂) различных элементов из С. Старейшим является алгоритм, вытекающий из следующей теоремы и в первоначальном варианте принадлежащий Сардинасу и Паттерсону [SarP].

Теорема 4.3. Пусть C - непустой язык над ∑. Определим индуктивно языки C₀, C₁, C₂, ... над ∑, полагая

Язык C является кодом тогда и только тогда, когда C_i∩C = ∅ для каждого i≥1.

Прежде чем перейти к доказательству теоремы, заметим, что в случае конечного языка C длина каждого слова в каждом C_i не превосходит длину самого длинного слова в C. Следовательно, существует лишь конечное число различных языков C_i, и мы действительно получаем алгоритм, определяющий, является ли множество C кодом (см. также упр. 1). Например, выберем в качестве С множество (4.1). В этом случае ;

Поскольку для каждого i≥1 C_i∩C = ∅, то C является кодом. С другой стороны, полагая C = {a, ab, ba}, получаем C₁ = {b}, C₂ = {a}. Так как C₂∩C ≠ ∅, то C не является кодом.

Доказательство. Сначала рассмотрим часть "тогда" утверждения теоремы. Покажем, что если C не является кодом, то одно из множеств C^* пересекает C.

Так как C не является кодом, то в C найдутся элементы x_v, удовлетворяющие (4.5). Ситуацию можно изобразить так:

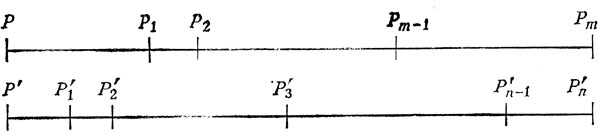
Идея состоит в том, что слово x_i1 ... x_im записывается на верхней прямой: отрезок PP₁ содержит x_i1, отрезок P₁P₂ содержит x_i2 и т. д. Аналогично слово x_j1, ... x_jn, записывается на нижней прямой. Поскольку x_i1 ≠ x_j1, точки P₁ и P₁' оказываются на разных вертикалях. (На схеме принято, что x_j1 является собственным префиксом x_i1.) Снова предполагая минимальность m в (4.5), мы можем заключить, что ни одна из точек верхней прямой (за исключением первой и последней точек) не лежит на одной вертикали с точкой нижней прямой.

Напомним, что слова из C_i+1 получаются либо стиранием префикса, принадлежащего C^*, в некотором слове из C, либо стиранием некоторого префикса, принадлежащего C, в слове из C_i. Таким образом, на нашей схеме слово в отрезке P₁'P₁ принадлежит C₁, слово в отрезке P'₂P₂ принадлежит C₂, слово в отрезке P₁P'₃ принадлежит C₃, а слово в отрезке P₂P'₃ принадлежит C₄. Рассуждая далее таким же образом, мы заключаем, что либо x_jn принадлежит одному из множеств C_i (это имеет место в описанной выше ситуации), либо x_im принадлежит некоторому множеству C_i (последнее имеет место в случае, когда P_m-1 ближе к общей концевой точке, чем P'_n-1). В любом случае одно из множеств C, пересекает C.

Рассмотрим теперь часть "только тогда". Предположим, что С является кодом. Прежде всего индукцией по i докажем, что

(4.9)

Действительно, для i = 0 утверждение (4.9) очевидно. (Напомним, что C₀ = C.) Предположим, что (4.9) выполнено для i-1, и рассмотрим w∈C_i, i≥1. По определению C_i найдутся слова x∈C и y∈C_i-1, такие, что

По предположению индукции x₁y = x₂ для некоторых x₁ и x₂ в C^*. Следовательно, либо x₁xw = x₁y = x₂, либо x₁yw = x₂w = x₁x в зависимости от того, какое из равенств (4.10) имеет место. В обоих случаях мы видим, что C^*w∩C^* ≠ ∅, а это завершает доказательство (4.9).

Чтобы показать, что C не пересекается ни с одним из множеств C_i, i≥1, предположим противное: C∩C_i ≠ ∅ для некоторого i≥1. Следовательно, по определению C_i найдутся такие слова x∈C, x'∈C и y∈C_i-1, что

Рассмотрим первое равенство. В этом случае (4.9) влечет yC^*∩C^* ≠ ∅ и C^*y∩C^*≠∅, откуда, согласно лемме 4.2, следует y∈C^*. Однако это невозможно, поскольку yx = x' и C есть код.

Следовательно, в (4.11) должно выполняться альтернативное равенство. Отсюда следует, что i≥2, поскольку в противном случае y принадлежало бы C, представляя собой произведение двух элементов из C. Следовательно, существуют y₁∈C_i-2 и x"∈C, такие, что

Первое равенство не выполняется, потому что в силу (4.9) и леммы 4.2 y₁x'x = x". Таким образом, должно выполняться альтернативное равенство

Если i = 2, то выходит, что некоторый элемент C можно записать как произведение трех элементов из C. Значит, i≥3.

Продолжая в этом духе, мы придем к тому, что i больше любого наперед заданного числа. Отсюда можно заключить, что для всех iC∩C_i = ∅. ▫