4.2. Максимальные коды

Код C над алфавитом ∑ называется максимальным, если для любого кода C'⊇C над ∑ имеет место C' = C. Например, код C = {aa, ab, ba, bb) является максимальным. Очевидно, для каждого слова w в алфавите {a, b} не из кода C множество C∪{w} не является кодом. Это заключение следует из того, что слово w² может быть разложено в произведение элементов из C∪ {w} двумя разными способами.

Максимальные коды можно охарактеризовать посредством некоторых числовых величин, связанных с языками. В теории языков такое описание класса языков - редкое явление.

Кодовым индикатором слова w в алфавите ∑ из n≥2 букв называется величина c_i (w) = n^-|w|.

Пусть L - язык над ∑, где ∑ содержит n≥2 букв. (Предполагаем, что ∑ - минимальный алфавит языка L, т. е. L не является языком ни над каким собственным подмножеством ∑.) Тогда кодовый индикатор языка L, обозначаемый через ci(L), определяется как сумма кодовых индикаторов всех слов в L. Таким образом, если язык L конечен, то ci(L) - положительное рациональное число. Если же язык L бесконечен, то ci(L) либо является положительным вещественным числом (если соответствующий ряд сходится), либо равно бесконечности.

Например, если L является языком (4.1), то

Ограничение кодового индикатора сверху соответствует двум интуитивным идеям: во-первых, код не должен содержать слишком много слов и, во-вторых, чем больше в языке коротких (а не длинных) слов, тем больше шанс, что этот язык не будет кодом. Это приводит нас к следующей теореме.

Теорема 4.4. Каждый код C удовлетворяет неравенству ci(C)≤1.

Доказательство. Сначала предположим, что С является конечным кодом в алфавите из т≥2 букв. Следуя определению кода, легко проверить, что каждая степень C^j, j≥1, также является кодом.

Теперь индукцией по j докажем, что

Для j = 1 это очевидно. Предполагая (4.12) для фиксированного значения j, рассмотрим степень C^j+1. Так как C^j+1 является кодом, каждое из его слов единственным образом можно представить в виде xw, где x∈C, а w∈C'. Если C состоит из слов x₁,..., x_t, а c_a = n^-|x_α| для α = 1, ..., t, то

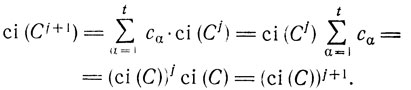
(Здесь используются предположение индукции и равенство

Следовательно, (4.12) верно.

Если длина самого длинного (соответственно самого короткого) слова в C равна K (соответственно k), то длина каждого слова в C^j ограничена числом k_j снизу и числом K_j сверху. Следовательно, существует не более чем (K - k)j+1 различных значений длины слов из C^j. С другой стороны, ci(L)≤1 для любого языка L, такого, что все слова в L имеют одинаковую длину. Эти факты приводят к оценке

Применяя (4.12), получаем, что (ci(C))^j≤(K - k)j + 1 для всех j. Так как K - k не зависит от j, это возможно лишь при ci(C)≤1.

Этот результат легко распространяется на случай бесконечного C. Очевидно, код C счетен: C = {x₁, x₂, ...}. Если ci(C)>1, то существует конечное подмножество C' = {x₁, x₂, ..., x_t} множества C, удовлетворяющее условию ci(C')>1, что противоречит первой части доказательства, поскольку подмножество кода также является кодом. ▫

Непосредственным следствием теоремы 4.4 и определения кодового индикатора является приведенный ниже результат.

Теорема 4.5. Код C, удовлетворяющий условию ci(C) = 1, является максимальным.

Следующая теорема показывает, что для конечных кодов справедливо обращение теоремы 4.5.

Теорема 4.6. Конечный код С максимален тогда и только тогда, когда ci(C) = 1.

Доказательство. В силу теоремы 4.5 достаточно показать, что конечный максимальный код C удовлетворяет условию ci(C) = 1. Снова предположим, что алфавитом кода C является S с числом элементов n≥2, а длина самого длинного (соответственно самого короткого) слова в C равна K (соответственно k).

Так как код C максимален, то слово y∈C^* обладает следующим свойством: для каждого x∈∑^* существует такое слово x'∈∑^*, что yxx'∈C^* (ср. упр. 4). Пусть p - достаточно большое натуральное число, и пусть x пробегает множество ∑^p. Тогда каждое слово

имеет длину, не меньшую |y|+p и не большую |y|+p+k. (Слово x' можно выбрать так, что |x'|<K.) Следовательно, существуют такие не зависящие от p положительные числа q₁ и q₂, что каждое из слов (4.13) (когда x пробегает ∑^p) принадлежит некоторому языку C^j, причем

Поскольку длина интервала изменения j линейно зависит от p, а число слов вида (4.13) равно n^p, то найдется такое не зависящее от p положительное число q₃, что некоторое множество C^j₀ содержит не менее q₃n^p/p слов вида (4.13).

Предположим теперь, что ci(C)<1. Применив соотношение (4.12), получим

(Напомним, что длины слов вида (4.13) не превосходят |y| + p + K.) Но это означает, что существует такое не зависящее от p положительное число q₄ что для всех (достаточно больших) p

(ci(C)^q₁p>q₄/p.

Последнее возможно только при ci(C)≥1, и мы пришли к противоречию. Следовательно, ci(C)≥1, а это в сочетании с теоремой 4.4 дает, что ci(C) = 1. ▫