6.2. Морфический генератор для контекстно-свободных языков

В этом разделе мы в явном виде построим такой контекстно-свободный язык L₀, что каждый контекстно-свободный язык L представим в виде h^-1(L₀), где h - некоторый морфизм. Говоря неформально, все возможные выводы всех контекстно-свободных грамматик в закодированном виде представлены в L₀; морфизм используется для того, чтобы выбрать конечные результаты соответствующих выводов.

Сначала вводится некоторая "нормальная форма" результатов для контекстно-свободных грамматик: мы покажем, что каждый контекстно-свободный язык может быть порожден грамматикой, продукции которой имеют специфическую форму. Нормальные формы, которые будут фигурировать в леммах 6.3 и 6.4, обычно называются нормальной формой Хомского и нормальной формой Грейбах соответственно. Для этих лемм будут даны только короткие описательные доказательства; читатель при желании может восполнить недостающие детали. Кроме того, более подробные доказательства приводятся в ряде работ, например в [Sa2]^*, Язык, не содержащий λ, мы для краткости будем называть λ-свободным языком. Рассматривая грамматики для обозначения нетерминалов (соответственно терминалов), мы применяем заглавные (соответственно строчные) начальные буквы латинского алфавита, которые могут быть снабжены индексами или штрихами.

^* (См. также [G1].- Прим. перев.)

Лемма 6.3. Каждый λ-свободный контекстно-свободный язык порождается грамматикой с продукциями только двух видов: A→BC и A→a.

Доказательство. Проведем серию преобразований данной грамматики, каждое из которых оставляет без изменений язык, порождаемый грамматикой, так что в конечном итоге мы придем к грамматике нужного вида. Очевидно, мы можем предположить, что данная грамматика имеет только один начальный символ Ы.

Начнем с устранения продукций вида A→λ. Для этого прежде всего определим множество U, состоящее из всех нетерминалов B, таких, что B⇒^*λ. Новое множество продукций состоит из всех продукций вида A→α₁, α₁≠λ, таких, что в исходном множестве существовала продукция A→α, и α₁ или совпадает с α, или получается из него удалением нескольких вхождений элементов из U.

По существу тем же способом можно избавиться от продукций вида A→B. Сначала определим для каждого нетерминала A множество U_A, состоящее из всех терминалов и нетерминалов x, таких, что A⇒^*x. (Напомним, что продукции вида A→λ уже устранены. Следовательно, в выводе A⇒^*x используются только сохраняющие длину продукции.) Теперь новое множество продукций состоит, во-первых, из всех продукций S→a, где a - терминал из множества U_s, и, во-вторых, из всех продукций B→y₁ ... y_n, где n≥2 и каждая буква y такова, что в исходном множестве продукций имелась продукция A→x₁ ... x_n, обладающая следующими свойствами:

(Очевидно, что A всегда принадлежит U_A. Терм {x_i} добавлен для того, чтобы учесть терминалы x_i.)

Заменим теперь в этих продукциях каждую терминальную букву а новым нетерминалом Aa и добавим к множеству продукций Aa→a для всех a. После этих преобразований наша грамматика содержит продукции лишь двух видов: A→a (только в них будут входить терминалы) и

Для каждой продукции (6.4), где n>2, введем новые нетерминалы C₁, ..., C_n-2 и заменим (6.4) продукциями

▫

Лемма 6.4. Каждый λ-свободный контекстно-свободный язык L порождается грамматикой с продукциями только трех видов: A▫aBC, A▫aB, A▫a.

Доказательство. Начнем с грамматики для L, которая имеет вид, указанный в лемме 6.3. Для представления множества продукций удобно использовать матричные обозначения. Предположим, что A₁, ..., A_n - нетерминалы нашей грамматики, причем A₁ - единственный начальный символ. Если

суть все продукции для A₁, то мы выразим этот факт в виде

Полагая V = (A₁, ..., A_n), мы можем теперь представить все множество продукций в матричной форме

где (i) T есть n-мерный вектор-строка, элементами которого являются суммы терминальных букв, и (ii) M есть (n×n)-матрица, элементами которой являются суммы нетерминальных букв. В (i) и (ii) могут входить "пустые суммы" ∅. Например, если продукции нашей грамматики суть

то матричным представлением будет

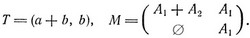
Наоборот, по данному матричному представлению для V (не обязательно имеющему вид (6.5)) мы можем написать продукции грамматики в обычной форме.

Модифицируем теперь (6.5) таким образом, чтобы результирующее матричное представление приводило исключительно к продукциям видов, указанных в лемме 6.4. С этой целью введем n² новых нетерминалов B_ij, 1≤i,j≤n, и квадратную матрицу Y = (B_ij). Рассмотрим грамматику

Здесь A₁ еще остается начальным символом. Продукции во втором множестве определяются естественным образом: правая часть продукции для B_ij образует (i, j)-й элемент матрицы M + MY.

Нетрудно видеть, что и грамматика (6.6) порождает наш язык L. По существу это происходит потому, что при использовании получающихся из VM продукций нетерминалы из V должны в конце концов заменяться терминалами. Эту идею выражает слагаемое TY в (6.6). С другой стороны, из Y можно вывести любую степень M, и поэтому переход к терминалам можно отложить настолько, насколько нужно.

Более формально, предположим, что слово w из языка L имеет длину t. С помощью итераций можно переписать (6.5) в виде

Так как слово w порождается (6.5) и |w| = t, мы заключаем, что w порождается грамматикой

(Продукции, получаемые из V→VM^*, можно использовать только в выводе слов длины больше t.) Аналогично, итерируя Y в (6.6), получаем

мы видим, что каждое слово, порождаемое (6.7), в частности слово w, порождается (6.6).

Обратно, (6.8) можно применить для доказательства того, что слово w длины t, порождаемое (6.6), принадлежит языку L.

Пусть Y⁽ⁱ⁾ (соответственно M⁽ⁱ⁾), i = 1, ..., n, обозначает i-ю строку Y (соответственно M). Запишем сначала (6.6) в

виде

Поскольку элементами M являются суммы нетерминалов, можно записать, что

где T⁽ⁱ⁾ есть (n×n)-матрица, все элементы которой суть либо λ, либо ∅. Это приводит (6.9) к виду

Наконец, применив V→T + TY к другим вхождениям V в (6.10), получим грамматику

очевидно, содержащую продукции только требуемого вида.▫

Определим теперь наиболее важные способы записи выводов, соответствующих контекстно-свободной грамматике.

Рассмотрим алфавит

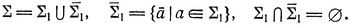
Отображение Дика ρ множества ∑^* в себя определяется равенствами

Предположим, что ∑₁ состоит из k≥1 букв a₁, ..., a_k. Язык Дика D_k определяется так:

Таким образом, D_k состоит из всех слов над ∑, которые можно свести к λ, применяя равенства

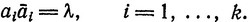
Если мы будем рассматривать a_i (соответственно a^-_i) как левую (соответственно правую) скобку некоторого типа, то D_k будет состоять из всех последовательностей правильно расставленных скобок. Например, полагая

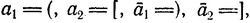
мы видим, что [( )[ ]]( ) принадлежит D₂, тогда как ([)] и ( ) [ ]] не принадлежат D₂.

Очевидно, что D_k порождается контекстно-свободной грамматикой, заданной продукциями

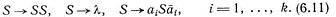
В дальнейшем мы будем иметь дело с языком Дика D₂, так как любые символы удобно кодировать двумя буквами. Весьма употребительным оказывается следующий язык:

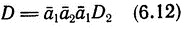
(так сказать, D₂ "с инициалами"). Язык D порождается слегка видоизмененной грамматикой (6.11): надо лишь добавить новый нетерминал S₁ (который будет единственным начальным символом) и продукцию 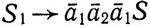. Предположим, что в (6.11) k = 2.

Инверсия σ^-1 конечной подстановки а действует на язык L так:

Заметим, что в общем случае σ(w) состоит из нескольких слов. Для того чтобы слово до принадлежало σ^-1(L), не обязательно, чтобы все эти слова принадлежали языку L; достаточно, чтобы одно из них принадлежало L. Заметим также, что алфавиты области определения и множества значений конечных подстановок, рассмотренных в гл. 5, были равны, а здесь они могут различаться.

Мы теперь можем получить первый основной результат о представлении. В утверждении приведенной ниже теоремы D означает язык (6.12). Не существенно, что мы ограничиваемся рассмотрением λ-свободных языков: языки, содержащие λ, порождаются аналогичным образом из D∪{λ}.

Теорема 6.5. Для каждого λ-свободного контекстно-свободного языка L существует такая конечная подстановка σ, что

Доказательство. Рассмотрим любой язык L, порождаемый грамматикой G, множество P продукций которой задано так же, как в лемме 6.4. Пусть

суть нетерминальный и терминальный алфавиты грамматики G, причем A₁ - единственный начальный символ. Напомним, что D - язык над алфавитом

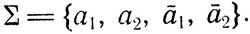
Интуитивно A_i кодируется как a₁a₂ⁱa₁, i = 1, ..., n. Слово 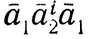используется для кодирования "инверсии" A_i и означает, что данное вхождение символа A_i опущено.

Формально определим конечную подстановку σ:∑^*_L→∑^* так:

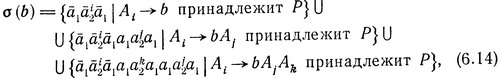
где b - любая буква из ∑_L, а i, j, k пробегают множество {1, ..., n). Нам еще нужно показать, что выполняется (6.13). Это проще всего сделать, установив несколько более сильное утверждение.

Обозначим через L_i, i = 1, .... n, язык, порождаемый продукциями P из начального символа A_i. Таким образом, мы будем рассматривать грамматики, полученные из G изменением начального символа; заметим, что L₁ = L. Мы установим следующее утверждение.

Утверждение. Пусть 1≤i≤n и w — любое слово над ∑_L. Тогда w∈L_i тогда и только тогда, когда σ (w) содержит какое-либо слово из

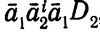(6.15)

т. е. тогда и только тогда, когда w∈σ^-1().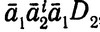

Прежде всего заметим, что (6.13) следует из нашего утверждения, если положить

i = 1. Доказательство утверждения ведется индукцией по длине t слова до. Можно предполагать, что t≥1: пустое слово не принадлежит ни одному из рассматриваемых языков (см. также упр. 5).

В качестве базиса индукции рассмотрим случай t = 1. В этом случае w принадлежит L_i тогда и только тогда, когда продукция A_i→w принадлежит P, а это имеет место тогда и только тогда, когда

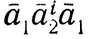∈σ(w). (6.16)

Поскольку 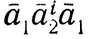является единственным словом из правой части (6.14), принадлежащим также языку (6.15), мы заключаем, что (6.16) выполняется тогда и только тогда, когда о (до) содержит слово из (6.15). Значит, слово до принадлежит L_i тогда и только тогда, когда σ(w) содержит слово из языка (6.15).

В качестве гипотезы индукции примем, что наше утверждение выполняется для всех слов, имеющих длину меньше t(≥2). Рассмотрим произвольное слово w, такое, что |w| = t.

Очевидно, что (i) w∈L, тогда и только тогда, когда или (ii) продукция A_i→bA_j принадлежит P и w можно записать в виде w = bw₁, где w_i∈L_j, или (ii)' продукция A_i→bA_jA_k принадлежит P и w можно записать в виде w = bw₂w₃, где w₂∈L_j, а w₃∈L_k.

По определению σ и по гипотезе индукции (ii) выполняется в том и только том случае, когда (iii) σ(b) содержит слово 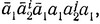а σ(w₁) содержит слово 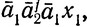где w = bw₁ и x₁∈D₂. Аналогично (ii)' выполняется в том и только том случае, когда (iii)' σ(b) содержит слово

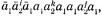
σ(w₂) содержит слово 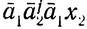и σ(w₃) содержит слово 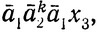где w = bw₂w₃, а x₂ и x₃ принадлежат D₂.

Для завершения шага индукции мы теперь покажем, что (iv) o(w) содержит слово из (6.15) тогда и только тогда, когда выполняется (iii) или (iii)'. Это доказывает, что условия (i) и (iv) эквивалентны, а это как раз то, что нам нужно.

Из определения D₂ непосредственно следует, что выполнение каждого из условий (iii) и (iii)" влечет выполнение условия (iv). Обратно, пусть выполнено (iv), т. е. σ(w) содержит слово

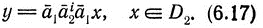
Пусть w = bw₁, где b - некоторая буква. Значит,

Напомним, что |w|≥2, а следовательно, w₁≠λ Значит, x≠λ. Равенство y = 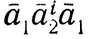не может иметь места, потому что в этом случае слово x = y₂ принадлежало бы D₂ и в то же время начиналось с "надчеркнутой" буквы (так как это слово принадлежит σ(w₁)), а эти два условия не могут выполняться одновременно. Значит, в силу (6.14) либо

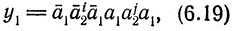
либо

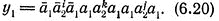
Достаточно показать, что из (6.19) (соответственно из (6.20)) следует (iii) (соответственно (iii)').

Предположим, что имеет место (6.19). Мы утверждаем, что

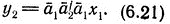
Согласно (6.17)-(6.19), это доказывает справедливость (iii), Действительно, если не выполняется (6.21), то

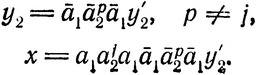
Очевидно, это приводит к ρ(x)≠λ для отображения Дика ρ независимо от y₂'. Последнее противоречит (6.17), что и доказывает равенство (6.21).

Пусть теперь выполняется (6.20). В этом случае мы утверждаем, что

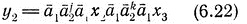
для некоторых x₂ и x₃ из D₂, где

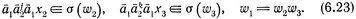
Очевидно, что (6.20), (6.22) и (6.23) доказывают истинность утверждения (iii)'.

Соотношения (6.22) и (6.23) являются следствиями следующих фактов. Слово y₂ должно начинаться с 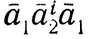это устанавливается точно так же, как в (6.21). Слово y₂ получается катенацией слов вида a₁a₂^pa₁ и 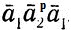, p = 1, ..., n. Согласно (6.20), слово y₂ должно содержать (после 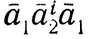) подслово 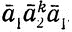поскольку в противном случае равенство ρ(x) = λ, не выполняется. Таким образом, мы получаем (6.22) и, снова рассматривая ρ, устанавливаем, что x₂, x₃∈D₂. Так как x₂ и x₃ принадлежат D₂ и, следовательно (если они непусты), должны оканчиваться "надчеркнутыми" буквами, мы получим разложение w₁ = w₂w₃, удовлетворяющее (6.23). ▫

Опираясь на теорему 6.5, теперь легко построить морфический генератор контекстно-свободных языков, упомянутый в начале этого раздела. Мы лишь так изменим определение (6.14), чтобы а оказалась морфизмом. Для этого достаточно образовать катенацию (т. е. последовательное приписывание) слов в правой части, предварительно разделив их граничными маркерами. В качестве граничного маркера используем символ +, чтобы напомнит, что мы имеем дело с "суммой" слов. Язык-генератор D надо модифицировать таким образом, чтобы обеспечить место для "мусора", возникающего от продукций, не используемых на каждом шаге.

Изложим теперь некоторые подробности более формально. Как и ранее, ∑ является алфавитом {a₁, a₂, 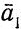, 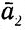). Язык L₀ над алфавитом

задается следующим образом:

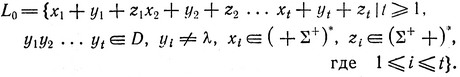
Легко показать, что язык L₀ контекстно-свободен; см. упр. 6.

Для данного λ-свободного контекстно-свободного языка L, как и в доказательстве теоремы 6.5, мы определим морфизм

следующим образом. Рассмотрим произвольную букву b из ∑_L. Пусть

есть множество слов, находящихся в правой части (6.14). Положим

Соотношение между σ и h устанавливается следующей леммой.

Лемма 6.6. Для каждого слова w над ∑_L слово h(w) принадлежит L₀ тогда и только тогда, когда σ(w) содержит слово из D.

Доказательство. Слова из L₀ имеют вид

причем в этих словах нет вхождений подслова ++ , кроме t-1 выделенных здесь вхождений. Поскольку все α₁ из (6.24) суть непустые слова над ∑, то подслово ++ не входит ни в одно h(b).

Ясно, что лемма справедлива для w = λ. Рассмотрим w = b₁ ... b_t, t≥1. Сначала предположим, что h(w)∈L₀ и запишем h(w) в виде (6.25). Тогда в силу (6.24) подслова ++ встречаются точно на границе между h(b_i) и h(b_i+1), i = 1, ..., t-1. По (6.24) y₁∈σ(b_i), i = 1, ..., t, а это показывает, что слово y₁ ... y_t из D принадлежит также σ(w).

Обратно, если o(bt) содержит слово y_i, i = 1, ..., t, такое, что y₁ ... y_t∈D. В силу (6.24) мы заключаем, что h(w) можно записать в виде (6.25), а это значит, что h (w) принадлежит L₀. Заметим, что мы учитываем тот факт, что y_i может быть первым или последним "слагаемым" в (6.24), поскольку в определении L₀ мы допускаем возможность равенств x_i = λ и z_i = λ. ▫

Мы хотим подчеркнуть, что выражение (6.25) для слова h(w) из L₀ ни в коем случае не обязано быть единственным: такое выражение может иметь место для разных y₁. Указанное обстоятельство отражает тот факт, что слово до может иметь в грамматике G несколько выводов. Этот момент подробнее исследуется в упр. 8.

Теорема 6.5 и лемма 6.6 показывают, что

Таким образом, мы установили фундаментальный результат, из которого следует, что L₀ является "морфическим генератором" для контекстно-свободных языков. Предположение о λ-свободности, как и в случае теоремы 6.5, не существенно: язык L₀∪{λ} подобным же образом оказывается генератором для контекстно-свободных языков, содержащих λ. (Очевидно, никакой язык не может порождать оба этих класса языков.)

Теорема 6.7. Для каждого λ-свободного контекстно-свободного языка L существует такой морфизм h, что