6.3. Порождение морфизмами рекурсивно перечислимых языков

Справедливость результата, аналогичного теореме 6.7, для семейства рекурсивно перечислимых языков следует из самого определения этого семейства. Действительно, каждый язык, слова которого могут быть перечислены посредством некоторой эффективной процедуры ("эффективной" в интуитивном смысле), порождается также грамматикой типа 0. Это утверждение (обычно называемое тезисом Чёрча^* будет использовано в приведенном ниже доказательстве, хотя последнее можно было бы провести и без него, см. упр. 10. Дальнейшее обсуждение тезиса Чёрча читатель может найти

^* (Точнее было бы назвать его тезисом Поста Подробнее о соотношении между вычислимостью и рекурсивной перечислимостью см. [УС*].- Прим. ред.)

Теорема 6.8. Существует язык L₀ типа 0 со следующим свойством: для каждого λ-свободного языка L типа 0 существует такой морфизм h, что L = h^-1(L₀).

Доказательство. Без потери общности можно считать, что языки типа 0 порождаются грамматиками, нетерминальные (соответственно терминальные) алфавиты которых являются собственными начальными отрезками бесконечного множества

с единственным начальным символом S₁. Пусть G₁, G₂, ... - перечисление всех таких грамматик в порядке возрастания общего числа вхождений всех букв в продукции. Каждой грамматике G₁ мы сопоставим слово вида

где p₁, p₂, ..., p_k суть продукции G_i. Таким образом, слова вида (6.27) содержат два специальных символа # и → и, кроме того, символы из (6.26). Все эти буквы кодируются теперь словами над алфавитом {a₁, a₂). (Например, можно представить все буквы в виде a₁aⁱ₂a₁. Значения i = 1, 2 зарезервируем для специальных символов, а остальные нечетные и четные значения i будем использовать для кодирования нетерминалов и терминалов соответственно.) Применяя такое кодирование к (6.27), получаем слово

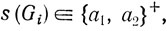
соответствующее грамматике G_i.

Для i≥1 определим теперь морфизм h_i: ∑^*_i→{a₁, a₂}^*, где ∑_i - терминальный алфавит G_i. Пусть b∈∑_i - произвольная буква, а e(b) - ее код (построенный, как указано выше) в алфавите {a₁, a₂). Положим

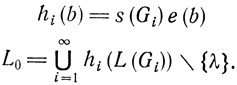
Язык L₀ эффективно перечислим, например, посредством процедуры, n-й шаг которой состоит в перечислении всех непустых слов, порождаемых грамматиками G₁, ..., G_n с выводами длины ≤n. Согласно тезису Чёрча, L₀ есть язык типа 0.

С другой стороны, если L = L(G_i) и λ∉L, то L = h_i^-1 (L₀). Этот результат получается сразу, поскольку "ярлык" s(G_i) наличествует только в тех словах из L₀, которые содержатся в L(G_i). ▫

Заметим, что при λ∈L язык h_i^-1(L₀) равен языку L\{λ}. Заранее нельзя сказать, какой из языков L(G_i) не содержит λ. На самом деле, проблема принадлежности λ данному языку L(G_i) неразрешима.

Как мы уже отмечали, теорема 6.8 обусловлена универсальной природой грамматик типа 0. Обсудим теперь некоторые более конкретные морфические представления языков типа 0. Оказывается, что множества совпадения очень полезны для таких представлений.

Мы хотим представить произвольный рекурсивно перечислимый язык как морфический образ множества совпадения. Этот результат давал бы представление всех рекурсивно перечислимых языков исключительно с помощью морфизмов! Само по себе это требование в какой-то мере слишком сильное по следующей причине. Каждый язык совпадения является "звездным языком", т. е. имеет вид L = L₁^* а, стало быть, звездными являются и языки h(L). Однако если мы предусмотрим надлежащий механизм для отбора подмножества из языка совпадения, то такое морфическое представление действительно окажется возможным. Очень простой способ, подходящий для этой цели, состоит в пересечении языка совпадения с регулярным языком. Этот способ широко используется в различных разделах теории языков. Другой возможный способ преодоления указанной трудности приведен в упр. 11.

Если ∑ и ∑₁ - алфавиты, ∑⊆∑_i, то морфизм H_∑: ∑₁^*→∑^* задается равенствами

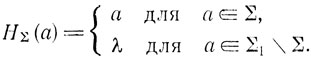
Таким образом, H_∑ стирает все, кроме букв из ∑.

Теорема 6.9. Для каждого рекурсивно перечислимого языка L⊆∑^*_T. существуют два морфизма h₁ и h₂ и регулярный язык R, такие, что

Доказательство. Рассмотрим произвольный рекурсивно перечислимый язык L, порожденный грамматикой G типа 0, где ∑_N и ∑_T - нетерминальный и терминальный алфавиты, S∈∑_N - начальный символ, а множество продукций P состоит из

p_i: α_i→β_i, i = 1, ..., n.

(Таким образом, мы каждой продукции приписываем ее имя p_i.)

По существу за конструкцией h₁, h₂ и R стоит следующая идея. Каждое слово в L является последним словом в некотором выводе D в рамках G. На слове D', похожем на D, морфизмы h₁ и h₂ удовлетворяют равенству

Однако h₁ "пробегает быстрее", чем h₂, префиксы D', и h₂ "догоняет" h₁ только в самом конце. Морфизм H_∑ стирает все, кроме конечного результата. Наконец, R гарантирует, что рассматриваются только слова соответствующего вида.

Изложим теперь подробности более формально. Мы используем "штрихованные варианты" алфавитов так же, как и ранее: ∑' есть алфавит {a'|a∈S}, а w' - слово, полученное из w приписыванием штриха каждой букве. Рассмотрим алфавиты

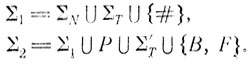
Морфизмы h₁, h₂: ∑₂^*→∑₁^* задаются таблицей

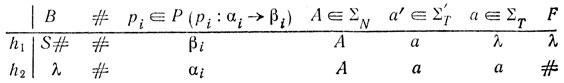
Далее, регулярный язык R задается регулярным выражением

Мы должны еще показать, что выполняется (6.28). Сначала приведем пример. Рассмотрим грамматику с продукциями

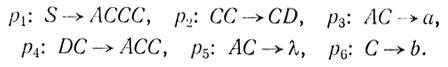
Слово ab принадлежит языку, порожденному этой грамматикой, что видно из вывода

Теперь поставим этому выводу в соответствие слово

и заметим, что H_(a,b)(w) - ab и что w ∈ R. Далее, h₁(w) = h₂(w), где обе части равны слову, полученному из (6.29) заменой ⇒ на # и добавлением # в конце.

Возвращаясь к доказательству, мы сначала покажем, что произвольное слово x∈L содержится также в правой части (6.28). Для этого нам нужно лишь доказать по индукции следующее утверждение: каждый раз, когда

является выводом в G, существует слово w∈B(V^*₁PV₁^*#)⁺, такое, что

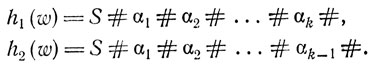
Очевидно, что этого достаточно, так как если α_k = x является терминальным словом,то

Для k=1 можно выбрать w = Bp₁#, где p₁ - имя продукции S→α₁. В качестве гипотезы индукции примем, что утверждение истинно для k. Значит, для произвольного вывода (6.30) существует слово w, удовлетворяющее требуемым условиям. Удлиним (6.30) дополнительным звеном

и продукция p: α→β принадлежит P. Пусть слово β'₁ (соответственно β₂) получается из β₁ (соответственно из β₂) приписыванием всем терминалам штрихов (при этом нетерминалы остаются без изменений). Тогда слово wβ'₁pβ'₂# удовлетворяет требуемым условиям для более длинного вывода. Это завершает шаг индукции.

Обратно, рассмотрим произвольное слово

Поскольку слово w∈R, его можно записать в виде

Заметим, в частности, что слово x должно стоять перед F, потому что x = H_∑T(w), а все буквы, не принадлежащие ∑_T, стираются морфизмом H_∑T.

Теперь используем равенство h₁(w) = h₂(w). Если w есть префикс w, то одно из слов h₁(w) и h₂(w) должно быть префиксом другого. Ситуация легко исследуется просмотром всех вхождений #. Буква В вносит одно вхождение # в h₁-образ, но не вносит ни одного в h₂2-образ. Каждое из слов w_i вносит одно вхождение # в конце h₁- и h₂-образов. Следовательно, h₁ "движется быстрее", т. е. h₂(w) является префиксом h₁(w).

В частности, имеем

для некоторых слов w_i⁽¹⁾, и, следовательно,

Так как h₂ "догоняет" h₁ при отображении xF, должно иметь место w_k⁽¹⁾ = x.

Слово w_i, i = 1, ..., k, дает "вклад" w_i⁽¹⁾# в h₁-образ и "вклад" w⁽ⁱ⁾_i-1 в h₂-образ. (Здесь мы полагаем w₀⁽¹⁾ = S.) Поскольку w_i∈V₁^*PV₁^*#, отсюда следует, что

где α→β - продукция в P. Но это означает, что мы имеем вывод

где w_k⁽¹⁾ = x, и, следовательно, x∈L.▫

Теорему 6.9 можно применить также для характеризации языков типа 0 при помощи весьма простого генератора. Такой генератор, называемый языком перетасовки двойников, мы сейчас определим.

Рассмотрим алфавит ∑ одновременно с его "подчеркнутым" вариантом ∑. (Как и в случае со штрихами, 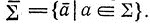При этом w обозначает слово, полученное из 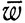надчеркиванием всех букв.) Язык перетасовки двойников L_∑ определяется равенством

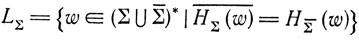
и, таким образом, состоит из слов, каждое из которых представляет собой произвольную перетасовку некоторого слова x∈∑^* и его "надчеркнутого" двойника 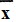. Если морфизм

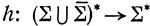
определен как

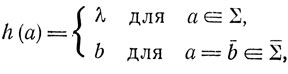
то очевидно, что L_∑ = E(h, H_∑).

Теорема 6.10. Для каждого рекурсивно перечислимого языка L⊆∑^*_T. существуют язык перетасовки двойников L_∑ и регулярный язык R₁, такие, что

Доказательство. Рассмотрим представление (6.28), данное в теореме 6.9. Можно считать, что ∑₂ и ∑₁, т. е. алфавиты области определения и множества значений морфизмов h₁ и h₂, не пересекаются. (Чтобы достичь этого, мы просто переименуем буквы ∑₁, что не окажет никакого влияния на (6.28).)

Положим теперь ∑ = ∑₂∪∑₁. Пусть g - морфизм, удовлетворяющий равенству

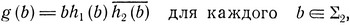
и пусть язык R₁ получается из языка g(R) введением в его слова букв из 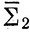в произвольном порядке. Таким образом, R₁ состоит из слов вида

здесь b_i - буквы из 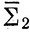, а x_j - - слова (возможно, пустые). Очевидно, язык R₁ регулярен.

Равенство (6.31) является теперь прямым следствием (6.28) и равенства

которое непосредственно следует из определений. ▫

В теореме 6.10 алфавит 2 зависит от языка L. Эта зависимость не существенна. Более сильные варианты этой теоремы приводятся в упр. 3 и 14.

Результаты, приведенные в этой главе, показывают, что язык двойной перетасовки и язык Дика играют похожие роли в теориях языков типа 0 и контекстно-свободных языков соответственно. В заключение мы без доказательства приведем следующую довольно своеобразную теорему о представлении (доказательство в общих чертах намечено в упр. 15). Символами ρ и D соответственно обозначаются определенные выше отображение Дика и язык Дика "с инициалами" (см. (6.12)). Что касается ρ, то мы рассматриваем надмножество исходного алфавита 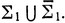Дополнительные символы в этом надмножестве не затрагиваются отображением ρ.

Теорема 6.11. Для каждого рекурсивно перечислимого языка L⊆∑⁺_T существует морфизм h, такой, что

L = ρ(h^-1(D))∩∑^*_T.