Упражнения
- Семейство 3 языков называется полным абстрактным семейством языков (АСЯ)*, если оно замкнуто относительно каждой из следующих операций: объединение, *(итерация), морфизм, инверсный морфизм и пересечение с регулярными языками. Докажите, что каждое полное АСЯ замкнуто также относительно катенации и конечной подстановки.
- Докажите, что семейства регулярных, контекстно-свободных и рекурсивно перечислимых языков являются полными АСЯ. (Наше соглашение - ограничить рассмотрение только А-свободными языками - здесь не применимо.) Докажите, что, с другой стороны, семейства DOL- и OL-языков являются "антиАСЯ", т. е. не замкнуты относительно ни одной АСЯ-операции. (Исчерпывающее изложение теории АСЯ читатель может найти в [G2]**.)
- Объясните, почему в формуле (7.2) фигурирует G1', а не G1 (Например, рассмотрите грамматику H1, заданную продукцией S→ab, грамматику H2, заданную продукциями S→ab, S→cd, и грамматику H3, заданную продукциями S→ab, S→ba. Какие следствия имела бы замена G1' на G1 в формуле (7.2)? Осталась бы верной лемма 7.3?)
- Сформулируйте и докажите соответствующий теореме 7.6 результат для семейства, всех регулярных языков (вместо рассмотренных в тексте Я-свободных).
- Рассмотрим семейство линейных языков, т. е. языков, порождаемых линейными грамматиками. Докажите результаты о линейной достаточности и линейной полноте, соответствующие лемме 7.5 и теореме 7.6. Эта теория значительно сложнее аналогичной теории для регулярных языков. При желании читатель может найти информацию в [MSW2].
- Обобщая рассуждения, использованные в доказательстве леммы 7.5, * покажите, что каждое грамматическое семейство замкнуто относительно пересечения с регулярными языками, Иначе говоря, если L - язык из этого семейства, a R - регулярный язык, то L∩R принадлежит семейству. Покажите также, что семейство языков, порожденное грамматикой только с одним терминальным символом, замкнуто относительно объединения. Зачем необходимо предположение об единственном терминале?
- Грамматическое семейство
 называется унарно-полным, если для любой грамматики G, удовлетворяющей условию
называется унарно-полным, если для любой грамматики G, удовлетворяющей условию 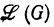 =
=  , существует a-ограничение Ga, удовлетворяющее условию
, существует a-ограничение Ga, удовлетворяющее условию  (Ga) =
(Ga) =  . Исследуйте понятие унарной полноты. (Теорема 7.6 показывает, что семейство регулярных языков унарно-полно. То же самое справедливо для линейных языков, см. упр. 5. Можно показать также, что семейство контекстно-свободных языков унарно-полно.)
. Исследуйте понятие унарной полноты. (Теорема 7.6 показывает, что семейство регулярных языков унарно-полно. То же самое справедливо для линейных языков, см. упр. 5. Можно показать также, что семейство контекстно-свободных языков унарно-полно.)
- Покажите, что конструкция в доказательстве теоремы 7.8 эффективна в следующем смысле. Предположим, известно, что
 1
1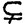
 2 и дан язык L, принадлежащий разности
2 и дан язык L, принадлежащий разности  2\
2\ 1. Тогда можно эффективно построить грамматическое семейство
1. Тогда можно эффективно построить грамматическое семейство  3, удовлетворяющее условию
3, удовлетворяющее условию  1
1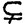
 3
3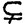
 2. (Проблема равенства грамматических семейств, т. е. проблема -выяснения, верно ли, что
2. (Проблема равенства грамматических семейств, т. е. проблема -выяснения, верно ли, что  (G1) =
(G1) =  (G2) в случае двух произвольно выбранных контекстно-свободных грамматик G1 и G2, остается открытой***.)
(G2) в случае двух произвольно выбранных контекстно-свободных грамматик G1 и G2, остается открытой***.)
- Покажите, что между любыми двумя семействами в иерархии (7.7) найдется некоторое цветосемейство. (Рассмотрите нечетное число "склеенных" вместе циклов.)
- Покажите, что семейство орграфов, ассоциированное с языком L = {ab, bc}, является последователем семейства орграфов, ассоциированного с языком {ab}. (Понятие последователя определяется здесь точно так же, как для цветосемейетв.) Покажите, что семейство орграфов, ассоциированное с L3 = {ab, bc, cd}, не является, однако, последователем семейства орграфов, ассоциированного с L2. Покажите, что семейство орграфов, ассоциированное с языком {ab, bc1, b1c1, b1c, cd}, является предшественником семейства, ассоциированного с L3. (См. в [MSW4] обсуждение соответствующих иерархий. Не известен ни один пример последователя, если орграфы более сложны, например содержат циклы.)
- Заметим, что каждый граф (соответственно орграф) является интерпретацией графа (соответственно, орграфа), содержащего петлю. Это основная причина того, почему такие графы и орграфы были исключены из рассмотрения. Покажите, что семейство орграфов, ассоциированное с языком {a2}, не имеет предшественника.
- Сопоставьте каждой контекстно-свободной грамматике некоторый конечный язык. Рассмотрите интерпретации такого языка наряду с интерпретациями исходной грамматики. Постройте коммутативную диаграмму, а также исследуйте ее отношение к семейству языков, порождаемых всеми интерпретациями исходной грамматики.
- Покажите, что цветосемейства образуют плотное частично упорядоченное множество, т. е. что между двумя любыми цветосемействами, одно из которых строго содержится в другом, существует строго промежуточное цветосемейство. Указания. Сначала рассмотрите произвольный циклический граф вида C2m+1. Покажите, что существуют произвольно большие связные графы H, такие, что (i) H является интерпретацией графа C2m+1, но не обратно и (ii) если отождествить две любые несмежные зершины в H, то C2m+1 окажется интерпретацией полученного графа. Заключите отсюда, что не существует графа, для которого граф C2m+1 был 5ы последователем. Распространите это заключение на произвольный связный граф G, в который C2m+1 входит как наименьший нечетный цикл, посредством "замещения" одного вхождения этого цикла графом H. После этого заключение легко распространить и на случай несвязных графов. (Это упражнение основано на частном сообщении Э. Велцля.)
* (В отечественной литературе такие семейства иногда называют полными многообразиями (см. также замечание 3° на с. 137).- Прим. перев.)
** (На русском языке имеется изложение теории АСЯ в ряде статей в сборнике [ЯиА*].- Прим. перев.)
*** (Относительно этого упражнения см. замечание 1° переводчика в конце главы.- Прим. ред.)
Замечания переводчика 1°. Алгоритмы для проблемы включения, а следовательно, и проблемы равенства грамматических семейств (г. с.) изложены в работе [GGoSp*]. Сначала выделяются три тривиальные г. c.: L∅ = {∅}, где ∅ - пустой язык, Lλ = {∅, {λ}}, Ltin = {L|L конечен}. В более ранней работе [CrGSp*] были предложены алгоритмы для решения проблем, порождает ли произвольно выбранная контекстно-свободная грамматика (КСГ) G г. с.: L∅, Lλ, Ltin и LCF - семейство всех контекстно-свободных языков (в последнем случае Саломаа называет КСГ G полной). Г. с.  называется собственным, если оно нетривиально и является собственной частью семейства LCF. Полным полуАСЯ называется семейство языков, содержащее непустой язык и замкнутое относительно морфизма, инверсного морфизма, пересечения с регулярными множествами и объединения. Для любого множества языков
называется собственным, если оно нетривиально и является собственной частью семейства LCF. Полным полуАСЯ называется семейство языков, содержащее непустой язык и замкнутое относительно морфизма, инверсного морфизма, пересечения с регулярными множествами и объединения. Для любого множества языков  через φ(
через φ( ) и F(
) и F( ) обозначаются соответственно наименьшее полное полуАСЯ и наименьшее полное АСЯ, содержащее
) обозначаются соответственно наименьшее полное полуАСЯ и наименьшее полное АСЯ, содержащее  . Полное полуАСЯ
. Полное полуАСЯ  называется главным, если существует язык L, такой, что
называется главным, если существует язык L, такой, что  = φ ({L}). В работе [CrG] доказан важный результат о том, что каждое нетривиальное г. с. является полным главным полуАСЯ. Алгоритм для решения проблемы включения г. с. в [GGoSp*] основан на методе разложения г. с. Определяются сумма г. с.
= φ ({L}). В работе [CrG] доказан важный результат о том, что каждое нетривиальное г. с. является полным главным полуАСЯ. Алгоритм для решения проблемы включения г. с. в [GGoSp*] основан на методе разложения г. с. Определяются сумма г. с.
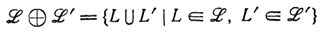
и их произведение
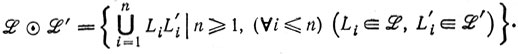
Выражение вида
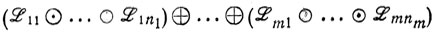
называется многочленом г. с. (sum-of-products). Если удаление из многочлена любого  ij приводит к многочлену, обозначающему строго меньшее Г. с, то многочлен называется минимальным. Г. с.
ij приводит к многочлену, обозначающему строго меньшее Г. с, то многочлен называется минимальным. Г. с.  называется простым (аддитивно простым), если для любых г. с.
называется простым (аддитивно простым), если для любых г. с.  1 и
1 и  2 из
2 из 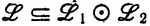 (соответственно
(соответственно 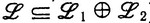 ) следует
) следует 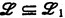 или
или 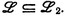 . Доказывается, что г. с. аддитивно просто тогда и только тогда, когда оно является конечным произведением нескольких простых г. с. Основным результатом является замечательная теорема простого разложения: каждое г. с. единственным образом (с точностью до переименования) представимо в виде минимального многочлена от простых г. с, причем этот многочлен можно эффективно найти по заданию исходного г. с. порождающей его грамматической формой. С помощью этой теоремы проблема включения г. с. сводится к частному случаю, когда первое г. с. просто, а второе является произведением простых. Для дальнейшего решения вводится еще одна операция
. Доказывается, что г. с. аддитивно просто тогда и только тогда, когда оно является конечным произведением нескольких простых г. с. Основным результатом является замечательная теорема простого разложения: каждое г. с. единственным образом (с точностью до переименования) представимо в виде минимального многочлена от простых г. с, причем этот многочлен можно эффективно найти по заданию исходного г. с. порождающей его грамматической формой. С помощью этой теоремы проблема включения г. с. сводится к частному случаю, когда первое г. с. просто, а второе является произведением простых. Для дальнейшего решения вводится еще одна операция 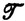 над г. е. Грамматика G = (V, ∑, P, σ) называется сплит-линейной (split linear), если правая часть каждой продукции в G принадлежит множеству
над г. е. Грамматика G = (V, ∑, P, σ) называется сплит-линейной (split linear), если правая часть каждой продукции в G принадлежит множеству
A(V-∑)∪C∪(V-∑)B,
где A, B, C образуют разбиение ∑. Для г. с.  1,
1,  2
2 3 через
3 через 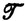 (
( 1,
1,  2
2 3) обозначается семейство языков вида τ(L), где L = L(G) для некоторой сплит-линейной грамматики
3) обозначается семейство языков вида τ(L), где L = L(G) для некоторой сплит-линейной грамматики
G = (F, A∪C∪B, P, σ),
а τ — такая подстановка на (A∪C∪B)*, что τ(x) принадлежит  1,
1,  2
2 3, если x принадлежит A, C или B соответственно. Собственное г. с. является простым тогда и только тогда, когда оно имеет одну из альтернативных форм
3, если x принадлежит A, C или B соответственно. Собственное г. с. является простым тогда и только тогда, когда оно имеет одну из альтернативных форм 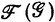 или
или 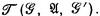 Семейство регулярных языков
Семейство регулярных языков 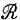 играет роль единицы относительно
играет роль единицы относительно 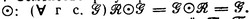 Оказывается, что любое г. с. строится из
Оказывается, что любое г. с. строится из 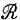 с помощью операций
с помощью операций 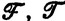
 и
и 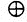 , причем его представление находится эффективно. Существует единственное каноническое представление, уточняющее представление в виде минимального многочлена. Два нетривиальных г. с. равны тогда и только тогда, когда совпадают их канонические представления. Включение г. с. также выводится из их канонических представлений. Каноническое представление дает большую информацию о структуре г. с., и, вероятно, с его помощью можно получить решение многих проблем, связанных с г. с. Было бы интересно распространить введенные понятия на произвольные полные полуАСЯ.
, причем его представление находится эффективно. Существует единственное каноническое представление, уточняющее представление в виде минимального многочлена. Два нетривиальных г. с. равны тогда и только тогда, когда совпадают их канонические представления. Включение г. с. также выводится из их канонических представлений. Каноническое представление дает большую информацию о структуре г. с., и, вероятно, с его помощью можно получить решение многих проблем, связанных с г. с. Было бы интересно распространить введенные понятия на произвольные полные полуАСЯ.
2°. Различные модификации схем грамматик, позволившие получить kC содержательные результаты, относящиеся к семействам языков, отличных от , а также к субрегулярным семействам, рассматриваются в работах [W], [MPSW*] и [OSW*].
3°. Естественно определяемые классы сложности языков обычно являются АСЯ, хотя и не полными (см. [АиЯ*] и замечание в конце гл. 6). Таким образом, контекстные языки образуют (просто) АСЯ и распознаются недетерминированными машинами Тьюринга с линейной памятью. Среди классов временной сложности аналогичную роль играет абстрактное семейство языков квазиреального времени (см. [Bea*]).
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'