7.3. Раскраски и семейства графов
Применим теперь идеи, изложенные в этой главе, к теории графов. Этот подход, появившийся совсем недавно, представляется особенно интересным по двум причинам. Во-первых, он приводит к классификации графов, основанной на понятии, естественным образом обобщающем понятие раскраски графа. Во-вторых, вопросы, связанные с этой классификацией, можно отождествить с вопросами, касающимися теории грамматических форм. Таким образом, мы обнаруживаем интересную связь между теорией языков и теорией графов.
Помимо орграфов, введенных в гл. 2, мы будем рассматривать и неориентированные графы, которые для краткости будем называть просто графами. По определению графом является пара (V, E), где V - конечное множество, элементы, которого называются вершинами, а E - множество неупорядоченных пар элементов V. Элементы E называются линиями или ребрами (в отличие от стрелок в случае орграфов). В дальнейшем предполагается, что графы и орграфы не содержат петель, т. е. ребер или стрелок, ведущих из вершины в нее же. Предполагается также, что каждый граф или орграф содержит хотя бы две вершины, связанные линией или соответственно стрелкой. Сначала рассмотрим непомеченные графы и орграфы и начнем с основных определений.
Граф G' называется интерпретацией графа G, если существует отображение φ множества вершин G' в множество вершин G, такое, что для каждого ребра в G', соединяющего вершины x и y, существует ребро в G, соединяющее вершины φ(x) и φ(y).
Орграф G' называется интерпретацией орграфа G, если существует отображение φ множества вершин Gr в множество вершин G, такое, что для каждой стрелки из x в y в орграфе G' существует стрелка из φ(x) и φ(y) в орграфе G.
Каждый граф (соответственно орграф) G определяет семейство  (G) графов (соответственно орграфов), состоящее из всех интерпретаций G. (Заметим, что мы применяем обозначение
(G) графов (соответственно орграфов), состоящее из всех интерпретаций G. (Заметим, что мы применяем обозначение  для семейства устройств, "машин" или "моделей"; такое же обозначение было введено для грамматик. Когда мы говорим о языках, порождаемых устройствами, то применяем обозначения
для семейства устройств, "машин" или "моделей"; такое же обозначение было введено для грамматик. Когда мы говорим о языках, порождаемых устройствами, то применяем обозначения  .)
.)
Мы будем говорить также, что граф G' является G-раскрашиваемым (или раскрашиваемым в соответствии с G), если G' принадлежит семейству  (G). Семейство графов называется цветосемейством, если оно равно
(G). Семейство графов называется цветосемейством, если оно равно  (G) для некоторого графа G.
(G) для некоторого графа G.
Введенная выше терминология мотивируется следующими соображениями. Для n≥2 обозначим через Kn полный граф с n вершинами, т. е. граф, в котором две любые различные вершины соединены ребром. Очевидно, что граф G n-раскрашиваем в обычном для теории графов смысле тогда и только тогда, когда G принадлежит  (Kn). Таким образом, знаменитая теорема о четырех красках утверждает, что каждый плоский граф принадлежит
(Kn). Таким образом, знаменитая теорема о четырех красках утверждает, что каждый плоский граф принадлежит  (K4)!
(K4)!
С другой стороны, в обычной теории раскрашивания графов рассматриваются только семейства  (Kn). Данное выше определение является намного более общим, поскольку рассматриваются раскрашивания, соответствующие произвольному графу.
(Kn). Данное выше определение является намного более общим, поскольку рассматриваются раскрашивания, соответствующие произвольному графу.
Например, рассмотрим циклический граф Cn с n вершинами, т. е. граф, ребра которого образуют замкнутый цикл. Следующая иллюстрация показывает, как граф C7 раскрашивается в соответствии с C5.
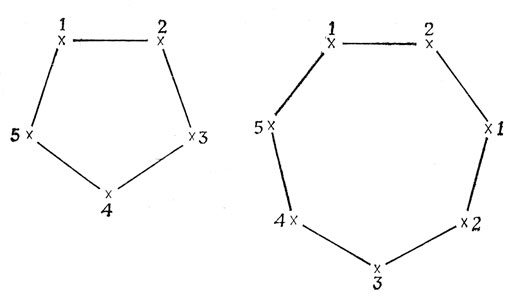
Таким образом, C7 принадлежит  (C5). Интуитивно, раскраска, соответствующая C5, означает такое использование цветов 1-5, что сохраняется соседство в C5: если вершина окрашена в цвет 1, то соседние с ней вершины могут быть окрашены в цвета 2 или 5, но не в 3 или 4 и т. д. Легко видеть также, что обратная раскраска невозможна: C5 не принадлежит
(C5). Интуитивно, раскраска, соответствующая C5, означает такое использование цветов 1-5, что сохраняется соседство в C5: если вершина окрашена в цвет 1, то соседние с ней вершины могут быть окрашены в цвета 2 или 5, но не в 3 или 4 и т. д. Легко видеть также, что обратная раскраска невозможна: C5 не принадлежит  (C7).
(C7).
Теперь обсудим значение введенных выше понятий теории графов с точки зрения теории языков. Отождествим конечный язык F с грамматикой G, заданной продукциями
S→w, w∈F,
и будем также говорить об интерпретации языка F, равно как о семействе языков  (F), порожденных F. Очевидно, язык L принадлежит
(F), порожденных F. Очевидно, язык L принадлежит  (F) тогда и только тогда, когда L является подмножеством σ(F) для некоторой конечной подстановки σ, такой, что σ(a) является конечным множеством букв для каждой буквы a и a≠b всегда влечет σ(a)∩σ(b) = ∅. Отождествление языка F и грамматики G проведено в соответствии с леммой 7.3, которая показывает, что семейство языков, определяемое грамматикой, порождающей конечный язык, полностью определяется этим языком.
(F) тогда и только тогда, когда L является подмножеством σ(F) для некоторой конечной подстановки σ, такой, что σ(a) является конечным множеством букв для каждой буквы a и a≠b всегда влечет σ(a)∩σ(b) = ∅. Отождествление языка F и грамматики G проведено в соответствии с леммой 7.3, которая показывает, что семейство языков, определяемое грамматикой, порождающей конечный язык, полностью определяется этим языком.
Приведенным вариантом G1 графа (орграфа) G называется граф (орграф), полученный из G удалением всех изолированных вершин, т. е. вершин, не связанных никаким ребром (стрелкой). Ясно, что  (G1) =
(G1) =  (G). (Напомним наше соглашение о том, что все графы и орграфы содержат хотя бы одно ребро или стрелку, и поэтому, удаляя изолированные вершины, мы никогда не удалим все вершины.)
(G). (Напомним наше соглашение о том, что все графы и орграфы содержат хотя бы одно ребро или стрелку, и поэтому, удаляя изолированные вершины, мы никогда не удалим все вершины.)
Конечный язык называется графоподобным, если он содержит только слова длины 2 и не содержит никаких слов вида a2. С каждым графоподобным языком можно естественным образом ассоциировать некоторый орграф: каждая буква обозначает вершину, а слова языка - стрелки. Например, является орграфом, соответствующим языку {ab, bc, ca}. Слово ab показывает, что существует стрелка, ведущая из a в b.
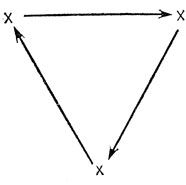
Обратно, приведенный вариант произвольного орграфа определяет графоподобный язык, единственный с точностью до переименования букв. Таким образом, между графоподобными языками и приведенными орграфами существует взаимно-однозначное соответствие*.
* (Это соответствие можно продолжить, сопоставив произвольным конечным языкам размеченные ориентированные гиперграфы.- Прим. перев.)
Указанная выше связь между графами и языками в явном виде выражается следующей леммой (доказательство леммы опускается, ибо она сразу следует из определений).
Лемма 7.9. Если F и F' - графоподобные языки, а G и G' - соответствующие им орграфы, то F' является интерпретацией F тогда и только тогда, когда G' является интерпретацией G.
Лемма 7.9 выражает коммутативность диаграммы
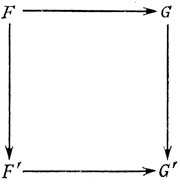
Таким образом, для произвольной интерпретации F' (графоподобного) языка F ассоциированный с F орграф является одновременно интерпретацией орграфа G, ассоциированного с F. Этот результат показывает также, что все вопросы относительно иерархий семейств орграфов можно свести к вопросам относительно семейств, порожденных графоподобными языками, и обратно.
Что касается графов, то их взаимосвязь с теорией языков аналогична. Единственное отличие состоит в том, что в данном случае мы вынуждены ограничиться рассмотрением "коммутативных языков", т. е. таких языков, в которых порядок букв несуществен. Например, не имеет значения, какое из слов ab и ba принадлежит языку: и то и другое означает, что в ассоциированном графе вершины a и b соединены ребром. Понятие интерпретации можно определить и для коммутативных языков. Например, коммутативный язык
{a1a2, a2a3, a3a4, a4a5, a5a6, a6a7, a7a1}
является интерпретацией коммутативного языка
{a1a2, a2a3, a3a4, a4a5, a5a1}
в соответствии с тем, что циклический граф C7 является интерпретацией 6. Вообще, для графов и коммутативных языков справедливо утверждение, соответствующее лемме 7.9.
Лемма 7.9 и ее аналог для графов показывают, что результаты леммы 7.1 можно применять к графам и орграфам. В частности, если G' - интерпретация G (где и G, и G' являются или графами, или орграфами), то  (G')⊂
(G')⊂ (G).
(G).
Вернемся теперь к обсуждению цветосемейств. Вспомним определения Cn и Kn, а также приведенный выше пример с C5 и C7. В соответствии с этими определениями легко установить следующую дважды бесконечную иерархию:
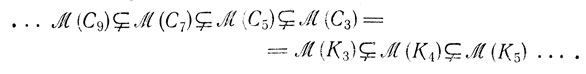
Очевидно, что для всех п имеет место равенство  (C'2n) =
(C'2n) =  (K2). (Оно соответствует тому обстоятельству, что граф является 2-раскрашиваемым в том и только том случае, когда он не содержит циклов нечетной длины.) Таким образом, существенно, что графы в (7.7), являющиеся циклами, имеют нечетную длину.
(K2). (Оно соответствует тому обстоятельству, что граф является 2-раскрашиваемым в том и только том случае, когда он не содержит циклов нечетной длины.) Таким образом, существенно, что графы в (7.7), являющиеся циклами, имеют нечетную длину.
Иерархия (7.7) является линейной иерархией цветосе-мейств (в общем случае цветосемейства не упорядочены линейно) . В действительности можно доказать следующий (сильнейший из возможных) результат о несравнимости.
Рассмотрим произвольный граф G. Если все циклы в G имеют четную длину, то  (G) =
(G) =  (K2). Это выводится, например, с помощью критерия 2-раскрашиваемости. Действительно, так как мы предположили, что все рассматриваемые графы имеют хотя бы одно ребро, то
(K2). Это выводится, например, с помощью критерия 2-раскрашиваемости. Действительно, так как мы предположили, что все рассматриваемые графы имеют хотя бы одно ребро, то  (K2) содержится в каждом цветосемействе.
(K2) содержится в каждом цветосемействе.
Итак, пусть в G имеется цикл нечетной длины 2n+1. Поскольку для некоторого m граф G является m-раскрашиваемым, получаем включения
 (C2n+1)⊆
(C2n+1)⊆ (G)⊆
(G)⊆ (Km).(7.8)
(Km).(7.8)
Значит, каждый граф G либо удовлетворяет (7.8), либо  (G) =
(G) =  (K2). В частности, каждое семейство
(K2). В частности, каждое семейство  (G) может быть несравнимо только с конечным числом семейств
(G) может быть несравнимо только с конечным числом семейств  (Ci) и конечным числом семейств
(Ci) и конечным числом семейств  (Kj). Оба этих числа могут быть произвольно большими, как показывает следующая теорема (ее доказательство опускается, так как необходимый для него теоретический аппарат выходит за рамки этой книги*).
(Kj). Оба этих числа могут быть произвольно большими, как показывает следующая теорема (ее доказательство опускается, так как необходимый для него теоретический аппарат выходит за рамки этой книги*).
* (Необходимые для доказательства сведения читатель может почерпнуть, например, из книг [О*], гл. 14, и [X*], гл. 12.- Прим. перев.)
Теорема 7.10. Для любых натуральных чисел m≥3 и n≥2 существует граф G, обладающий следующими свойствами:
(i) G является интерпретацией графа Km, но не графа Km-1;
(ii) C2n-1 не является интерпретацией графа G.
Следовательно, каждое из цветосемейств
 (C2n-1), ...,
(C2n-1), ...,  (C3)
(C3)  (K3), ...,
(K3), ...,  (Km-1)
(Km-1)
несравнимо с  (C).
(C).
По аналогии с грамматическими семействами мы назовем цветосемейство  (G2) последователем цветосемейства
(G2) последователем цветосемейства  (G1), если
(G1), если  (G1)
(G1)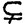
 (G2) и не существует цветосемейства
(G2) и не существует цветосемейства  (G3), такого, что
(G3), такого, что
 (G1)
(G1)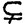
 (G3)
(G3)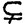
 (G2).
(G2).
Напомним, что мы исходили из того, что в каждом графе имеется хотя бы одно ребро. Если отказаться от этого предположения, то, исследуя граф K1 с одной вершиной и без ребер, можно непосредственно убедиться в том, что  (K2), является последователем
(K2), является последователем  (K1).
(K1).
Этот тривиальный пример является единственным возможным примером последователя, т. е. цветосемейства образуют плотное частично упорядоченное множество. Последнее обстоятельство используется в упр. 9 и 13; примеры последователей среди семейств орграфов приводятся в упр. 10.
Наконец, мы хотим показать, как подобные идеи можно применить в более общей ситуации. Например, можно рассмотреть размеченные графы, и в частности конечные (недетерминированные) автоматы, введенные в гл. 2. Предположим далее, что в каждом автомате имеются ровно одна начальная вершина q1 и ровно одна заключительная вершина q2, q1≠q2 и что ни одна стрелка не ведет в q1 и не выходит из q2. Предоставляем читателю проверить, что автоматом такого типа может быть представлен каждый λ-свободный регулярный язык.
Пусть автоматы G' и G относятся к описанному выше типу. Мы назовем автомат G' интерпретацией автомата G, если существует такое отображение φ множества вершин G' в множество вершин G и такое отображение ψ множества символов, помечающих стрелки G', в множество символов, помечающих стрелки G, что для каждой помеченной символом а стрелки из x в y в графе G' найдется помеченная символом ψ(a) стрелка из φ(x) в φ(y) в графе G и, кроме того,
φ(q1) = q1, φ(q2) = q2
и никакие другие вершины графа G' не отображаются посредством ψ в q1 или q2. Это определение расширяет определение, данное выше: оно требует также, чтобы сохранились пометки стрелок, равно как и начальная, и заключительная вершины.
С другой стороны, каждому такому автомату G можно сопоставить конечный язык F, состоящий из слов вида qaq'. (Слово qaq' показывает, что в автомате G некоторая помеченная символом а стрелка ведет из вершины q в q'. Предполагается, что в G нет изолированных вершин.) Пусть F и F' - два таких конечных языка; мы скажем, что F' является интерпретацией F, если (i) F' является подмножеством σ(F), где σ - конечная подстановка, определенная, как и выше, и (ii) aσ(q1)= {q1}, σ(q2) = {q2} и вершины q1, q2 больше нигде не встречаются в области определения σ.
Нетрудно проверить коммутативность следующей диаграммы:
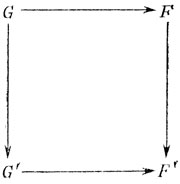
Эту диаграмму, как и предыдущую, можно записать, начиная с F.
Обозначим через 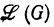 семейство языков, представимых интерпретациями графа G. Следует подчеркнуть, что семейства
семейство языков, представимых интерпретациями графа G. Следует подчеркнуть, что семейства  (F) не находятся больше во взаимно-однозначном соответствии с семействами
(F) не находятся больше во взаимно-однозначном соответствии с семействами  (G). Может иметь место
(G). Может иметь место  (G1) =
(G1) =  (G2), хотя соответствующие семейства
(G2), хотя соответствующие семейства  (F1) и
(F1) и  (F2) несравнимы.
(F2) несравнимы.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'