О пользе догадок (Глава шестая)

Молодой кавалер проигрался в Монте Карло. Верный выигрыш или смерть - только два события могли спасти его от позора, Размышляя о своей несчастной судьбе, он вспомнил рассказ о старой гра фине, доживающей свой век в Париже. Однажды в молодости она попала в столь же критическое положение и с успехом вышла из него, узнав секрет 'верного' номера. Движимый отчаянием, кавалер устремился в Париж. Ночью он пробрался в спальню графини, напугав бедную старушку до полусмерти. Когда графиня пришла в себя, она увидела молодого человека, который стоял перед ней на коленях и заплетающимся языком умолял спасти его жизнь и честь, открыв тайну верного номера.
- О господи это же так просто! - воскликнула старушка, - Три числа: шесть, девять и двенадцать, всегда были для меня исключительно счастливыми, родилась девятого декабря 1806 года, а на балу, когда мою голову венчала диадема с девятью крупными рубинами и двенадцатью бриллиантами, вделанными в шесть золотых колец, я затмила всех своих соперниц... Конечно, такие совпадения не могли быть случайными. Я получила прекрасное воспитание и не чужда натурфилософии, поэтому я сразу догадалась, что самым счастливым для меня числом должно быть среднее этих трех чисел. Сложив их, я получила двадцать сечь, а поделив на три - восемь. Затем без малейших колебаний несколько раз подряд я поставила на восьмерку.
Также без малейших колебаний мы называем эту главу о пользе догадок перефразируя тем самым заглавие знаменитой книги Якоба Бернулли^*.

(Имеется в виду книга Якоба Бернулли "Искусства догадок" опубликованная в 1713 г. и посвященная теории вероятностей.)

История знает не одну попытку использовать математику в азартных целях, причем многие из них мало чем отличались от ухищрений графини, не знавшей таблицы умножения. Но об этом речь впереди. А пока подведем некоторые итоги сказанному в предыдущей главе. Ознакомившись достаточно подробно с системами автоматического регулирования, мы получили возможность сформулировать несколько положений, имеющих принципиальное значение.

Мы установили, что цель управления - заставить некоторую систему совершать последовательность действий, предписанных про-граммой, или планом. В предыдущей главе рассматривались примеры, где подобные действия сводились лишь к механическим перемещениям, хотя в одном случае конечным результатом механических перемещений были музыкальные произведения, исполняемые виртуозами. Теперь мы расширим понятие цели и будем считать действиями все, что совершает искусственная или естественная система, включая, например, последовательность ответов на задаваемые человеку вопросы. Заметим попутно, что данная книга также появилась как результат последовательности действий, каждое из которых состояло в написании очередного слова или, если угодно, буквы. Эти действия также совершались по определенному плану.

Сказанное дает нам право определить процесс управления как всякий процесс, ведущий к достижению цели, т. е. заставляющий систему выполнять запланированные действия. Вопрос о том, всегда ли план или программа задается системе извне или же план может представлять со.бой внутреннее свойство самой системы, мы пока оставим открытым.

Рассматривая швейную машину и ПИД-регулятор, мы. пришли к выводу, что существуют по меньшей мере два принципиально различных способа организации процесса управления. Первый из них реализуется в швейной машине, которую мы отнесем к классу автоматических систем разомкнутого типа, К этому классу принадлежит большое количество разнообразнейших автоматических устройств и в том числе знаменитые ткацкие станки Жаккарда, продукция которых хорошо известна любой моднице. В разомкнутой автоматической системе каждая движущаяся деталь жестко связана с приводом (таких приводов в общем случае может быть несколько) и совершает движения, заранее определенные конструкцией системы. Результат движения никак не контролируется. Например, если в швейной машине сломается иголка или в ткацком станке порвется нитка, все детали будут продолжать двигаться до тех пор, пока человек не исправит повреждения.

В случае ПИД-регулятора также имеется жесткая программа действий: Однако в остальном организация работы принципиально иная. До тех пор пока фактические действия системы не отличаются от заданных, управление полностью отсутствует. Процесс управления проявляет себя только тогда, когда. обнаруживается отклонение от намеченного плана. При этом возникает то, что мы назвали выше управляющим воздействием, и управляющее воздействие всегда направлено противоположно причине, вызвавшей отклонение. Другими словами, имеется связь между результатом действий системы и той ее частью, которая побуждает систему совершать действия. Эту связь мы назвали обратной. Системы с обратной связью мы назовем системами замкнутого типа.

Мы установили, наконец, что в реальных физических системах между моментом, когда создаются условия для выполнения того или иного действия, и моментом совершения самого действия всегда проходит определенное время. Поэтому принцип отрицательной обратной связи был бы вообще порочным (мы-бы всегда опаздывали), если бы не додумались с помощью дифференцирующего звена определять как момент времени, когда создаются условия для отклонения, так и направление этого отклонения.

Наличие двух возможных способов построения автоматических систем приводит нас к совершенно естественному, хотя и несколько наивному вопросу: какой же из способов лучше? Действительно, вряд ли у нас есть основания предъявлять какие-либо претензии к конструкции швейной машины, верно служащей человеку уже более сотни лет. Правда, автомат для игры на рояле не удовлетворяет наши эстетические запросы, но на это легко возразить, что на сегодня вообще не существует искусственной системы,, замкнутой или разомкнутой, которая могла бы полностью заменить талантливого пианиста.

Признаемся сразу, что мы не собираемся отвечать здесь на этот вопрос, поскольку такого ответа попросту не существует. В определенных условиях лучшими оказываются системы разомкнутого типа, а в других условиях - замкнутого. Однако сама постановка вопроса позволит нам прийти в конечном итоге к достаточно интересным выводам.

Обратим внимание прежде всего на то, что при прочих равных условиях разомкнутая система должна быть обязательно сложнее замкнутой. А как же иначе? Ведь в разомкнутой системе все без исключения движения составляющих ее частей определяются конструкцией, т. е. являются вынужденными. В противоположность этому в замкнутой системе многие действия совершаются как бы сами по себе, а механизм управления включается лишь тогда, когда обнаруживается отклонение.

Но сложность, конечно, не такой уж большой порок. Значитель но важнее другое. Чтобы дальнейшее стало более ясным, рассмотрим, например, одну из возможных конструкций механизма привода рычага, в котором закреплена иголка швейной машины (рис. 29). Положение этого механизма, изображенное на рисунке, соответствует крайнему верхнему положению иглы. В этом положении вертикальная составляющая скорости рычага равна нулю. Вал с кривошипом вращается равномерно в направлении, показанном стрелкой. В момент, когда вал повернется точно на 90° по отношению к положению, показанному на рисунке, вертикальная составляющая скорости рычага с иглой достигает максимального значения. Поскольку рычаг обладает массой, он будет и в дальнейшем стремиться сохранить эту скорость, т. е. будет стремиться отклониться от движения, предусмотренного планом. Но конструкция кривошипного механизма препятствует такому отклонению и скорость рычага начнет уменьшаться, пока не станет равной нулю в крайнем нижнем положениииглы.

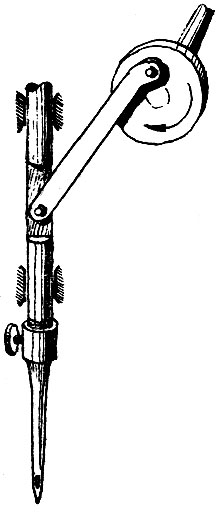
Рис. 29 Одна из возможных конструкций механизма привода рычага, в котором закреплена иголка швейной машины

Сказанное приводит нас к выводу, что конструкция механизма привода рычага предусматривает возможность отклонения и выполнена так, чтобы это отклонение никогда не могло иметь место. То же самое распространяется и на конструкцию любой системы, построенной по разомкнутому принципу.

Но вот тут-то и возникает важнейший вопрос: все ли отклонения можно предусмотреть заранее? Можно ли, например, построить швейную машину, которая представляла бы собой систему разомкнутого типа и при этом автоматически останавливалась каждый раз, когда ломается игла? Конечно, нет. Ведь для этого надо заранее хотя бы приближенно знать момент времени, когда произойдет поломка иглы, а этого не знает никто. Одна игла может сломаться через несколько минут после начала работы, а другая служит своей хозяйке многие годы. Поломка иглы - это случайное событие. Такими же точно случайными событиями являются, например, увеличение люфта в шарнирах рычагов, связывающих клавишу рояля с молоточком, или внезапное снижение нагрузки тепловой электростанции, причиной которому послужило то, что множество телезрителей захотели спать и одновременно выключили свои телевизоры. Именно наличие внешних воздействий, имеющих случайных характер, и вынуждает строить замкнутые автоматические системы с обратной связью.

В паровой машине, снабженной регулятором Уатта, изменение положения грузов регулятора может произойти, вообще говоря, по двум различным причинам: либо вследствие случайного изменения нагрузки, либо вследствие того, что изменение скорости вращения вала предусмотрено программой работы, такое изменение в программе мы также вправе считать случайным, поскольку паровая машина, грубо говоря, не знает плана своей работы во всех деталях.

Сказанное позволяет нам рассмотреть работу обратной связи под совершенно новым углом зрения. Автоматическая система подвержена случайным внешним воздействиям. Задача обратной связи состоит в том, чтобы в ответ на каждое такое воздействие вырабатывать свое собственное управляющее воздействие, устраняющее последствия возмущения.

А что делает игрок, играя в азартные или неазартные игры? Какова бы ни была игра, каждый участвующий в ней имеет дело с одним или с несколькими противниками. Если бы все действия противника были в точности известны игроку наперед, игра потеряла бы всякий интерес. Смысл игры в том и состоит, что, делая ход, игрок отвечает на предыдущий ход противника, который не был ему известей или, во всяком случае, был известен не в полной мере до того, как он был совершен. Окончательный результат игры зависит от того, насколько удачными были ходы игрока.

Для пущей убедительности рассмотрим еще один пример. Пусть имеется тепловая электростанция с паровой турбиной, питающая в числе прочих потребителей некое промышленное предприятие. Величина напряжения, вырабатываемого генератором, зависит от скорости вращения вала паровой машины. Машина снабжена регулятором, который и выступает теперь, с нашей новой точки зрения, в качестве игрока. Цель такого игрока - удерживать скорость вращения вала постоянной. Если он играет плохо, то скорость, например, может понизиться, что повлечет за собой понижение напряжения и очевидным образом снизит производительность питаемого промышленного предприятия. К еще более серьезным последствиям может привести увеличение сверх определенного предела скорости вращения вала, так как чрезмерное повышение напряжения вызовет перегрев и сгорание обмоток электродвигателей. Следовательно, всякий неудачный ход игрока приводит в этом примере к убытку (проигрышу), имеющему непосредственное денежное выражение. Аналогия с азартной игрой оказывается здесь полной.

В чем же состоит искусство игрока, играющего в азартные игры? Всякий скажет - искусство это в том, чтобы предугадать ход противника и сделать собственный ход так, чтобы добиться при этом максимального выигрыша. Именно этим и занимается дифференцирующее звено ПИД-регулятора. Изменяя ускорение маховика, оно заранее предугадывает возможные изменения скорости.

Неужели простой кусочек металла, прикрепленный к маховику двумя пружинками, и заключает в себе ту великую тайну, которой тщетно добивался кавалер у старой графини? Конечно, нет. Ведь хороший игрок всегда предусматривает развитие партии на несколько ходов вперед. Что же касается дифференцирующего звена, то оно способно предсказать лишь один ближайший ход, да и то только в такой простой системе, как паровая машина. И в то же время вскрытая нами здесь аналогия оказывается чрезвычайно плодотворной.

Последовательность ходов, которые совершает игрок, называется стратегией. С любой, даже достаточно простой игрой обычно связано множество возможных стратегий для каждого игрока. В процессе игры, основываясь на сведениях об уже совершенных ходах и предугадывая следующие, игрок меняет свою стратегию, добиваясь максимального выигрыша.

Развивая обнаруженную нами аналогию, мы вправе говорить теперь и о стратегии управления. Стратегия ПИД-регулятора состоит в том, чтобы предугадывать один ближайший возможный ход противника и определять на основании этого свой собственный ход, который состоит в том, чтобы приоткрыть или закрыть заслонку. И дело совсем не в том, насколько эффективной оказывается такая стратегия. Мы уже установили в предыдущей главе, что ПИД-регулятор - игрок довольно слабый. Стоит ему столкнуться с достаточно изощренным противником, как он, подобно многим другим игрокам в азартные игры, начинает беспорядочно метаться из стороны в сторону, то завышая, то занижзя ставки, и это неизбежно ведет к проигрышу.

И в то же время установленная нами аналогия совместно с рассмотренной в предыдущей главе идеей включения дифференцирующего, а заодно и интегрирующего звеньев в цепь обратной связи открывает новое и совершенно неожиданное свойство замкнутых автоматических систем. Оказывается, в цепь обратной связи можно включать органы, задающие стратегию управления или, если угодно, стратегию игры с природой. А как мы вскоре увидим, и не только с природой.

Еще один пример мы посвятим также весьма азартному занятию - охоте. Как ведет себя охотник, стреляющий по летящей утке? Сначала он прицеливается, т. е. представляет себе воображаемую линию, являющуюся продолжением оси ружейного ствола. Затем, когда положение этой линии в пространстве, на его взгляд, оказывается таким, как нужно, он нажимает на собачку. Химическая энергия, заключенная в порохе, освобождается, и под действием этой энергии заряд вылетает из ствола и движется в пространстве вдоль некоторой линии, называемой траекторией. Если расчеты охотника оказались правильными, го в некоторой точке пространства и в нужный момент времени траектория заряда и траектория летящей утки пересекаются.

Однако, как это хорошо известно всем охотникам, для того чтобы выстрел оказался успешным, нужно учесть, по меньшей мере, два обстоятельства. Первое состоит в том, что заряд летит с определенной скоростью и пройдет определенное время, пока он достигнет точки пересечения траекторий. За это время утка, хотя ее скорость, конечно, значительно меньше скорости заряда, также пролетит некоторое расстояние. Поэтому всякий опытный охотник целится не в ту точку, где утка находится в данный момент, а в другую, находящуюся несколько впереди по направлению полета утки. Расстояние между положением утки в данный момент и точкой прицеливания называется упреждением. Упреждение должно быть, очевидно, тем больше, чем дальше от утки находится охотник.

Во-вторых, как известно,, заряд летит в пространстве не по прямой, а по линии, называемой параболой. Поэтому, даже стреляя по неподвижной мишени, охотник должен целиться не в саму мишень, а несколько выше - давать завышение, которое опять-таки должно быть тем большим, чем дальше от цели находится охотник. Если стрельба производится не из охотничьего ружья, а из винтовки, завышения давать не нужно, поскольку оно учитывается конструкцией прицела. Тем не менее, завышение учитывается перед выстрелом путем установки прицельной рамки в соответствии с расстоянием.

Легко увидеть здесь все уже знакомые нам элементы. С помощью глаза (датчик) охотник устанавливает положение цели. По линии связи (нервная система охотника) данные о положении цели передаются усилителям (мышцы), которые с помощью исполнительною механизма (руки) устанавливают нужное положение ствола. Обычно перед выстрелом охотник некоторое время, как говорится, ведет стволом, изменяя его направление в соответствии с изменениями положения утки, а эти изменения воспринимаются датчиком (гдаз).

Следовательно, снова замкнутая система. В данном случае движение исполнительного органа (ствола) определяется планом, а этот план задается движением цели. Однако последний пример имеет одно принципиальное отличие от всех примеров, рассмотренных выше. Дело в том, что начиная с момента нажатия собачки, система регулирования (охотник) полностью теряет контроль над объектом регулирования (летящий заряд). Перемещение заряда в пространстве совершается под воздействием поля тяготения Земли, а также таких случайных возмущений, как, например, ветер, и изменить направление этого перемещения охотник при всем своем желании уже не в силах. Существенно здесь то, что автоматическая система бездействует не потому, что отсутствуют отклонения, как это было во всех примерах, разобранных выше, а потому, что возможность управления отсутствует в силу специфических особенностей самой системы. Выстрел окажется успешным только в том случае, если охотник правильно рассчитал точку встречи заряда и цели. Такой расчет производится в предположении, что траектория полета утки, вообще говоря, не изменится в течение ближайшего времени. Охотник ведет стволом именно для того, чтобы определить эту траекторию и рассчитать (экстраполировать) продолжение траектории.

Предположение о том, что утка будет продолжать лететь по той же самой траектории, как правило, оказывается достаточно обоснованным. Ведь в подавляющем большинстве случаев утка не подозревает о наличии охотника. Однако, если по каким-то своим утиным делам она в момент нажатия на собачку вздумает изменить направление полета, выстрел почти наверняка окажется неудачным для охотника.

Аналогичная ситуация возникает и при стрельбе из зенитных орудий по самолетам. Правда, здесь положение резко усложняется тем, что летчик, попавший в зону зенитного огня, начинает совершать так называемый противозенитный маневр, т. е. изменяет траекторию полета самолета по возможности случайным образом. Снова мы имеем аналогию с игрой, правда, в этой игре ставки неизмеримо выше. Стратегия одного из игроков - это последовательные изменения направления ствола оружия и определение момента времени, когда надо сделать ход (выстрел). Стратегия другого игрока в том, чтобы должным образом менять направление полета. Участвует в этой игре и третий игрок - ветер. На первый взгляд, у третьего игрока в отличие от первых двух нет определенной цели и поэтому включение его в число играющих вызывает сомнения. Ведь не считаем же мы игроком колоду карт, хотя расположение карт в этой колоде очевидным образом сказывается на протекании игры. К этому вопросу мы еще вернемся Существенным в последнем примере является то, что в определенных ситуациях предугадать даже ближайший ход противника оказывается значительно сложнее, чем в случае паровой машины.

Обобщим теперь все полученные сведения, снова привлекая концепцию черного ящика. Так, мы имеем два вида систем: разомкнутые и замкнутые. Заметим, что мы сознательно не говорим здесь автоматических, поскольку пока что мы не установили никаких различий между поведением живого игрока и ПИД-регулятора. Моделью разомкнутой системы может служить схема, показанная на рис. 30. Она состоит из носителя Н, на котором зафиксирован план, или программа, работы. План с носителя прочитывается датчиком и передается по каналу связи к усилителю. Выходной сигнал усилителя приводит в действие исполнительный механизм.

Носитель с зафиксированной на нем программой - вот то новое, что мы внесли в модель на рис. 30 по сравнению со всеми ранее рассмотренными моделями. Включая такрй носитель в состав системы, мы можем говорить уже о системе управления, а не о системе регулирования, как это было раньше. Следовательно, разомкнутая система управления содержит в своем составе четыре знакомых нам элемента и, кроме того, носитель. Главная и единственная отличительная черта разомкнутой системы состоит в том, что в ней отсутствует обратная связь между исполнительным механизмом и датчиком.

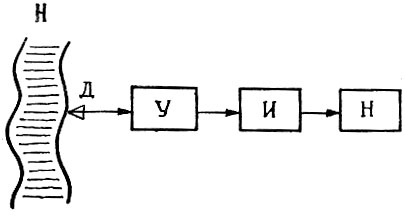
Рис. 30 Моделью разомкнутой системы может служить схема

Модель замкнутой системы управления показана на рис. 31. Кроме перечисленных элементов, здесь введен еще один дополнительный элемент, определяющий стратегию управления, - носитель с зафиксированной на нем программой. В остальном модель на рис. 31 не отличается от рассмотренных раньше и, следовательно, не требует дополнительных пояснений.

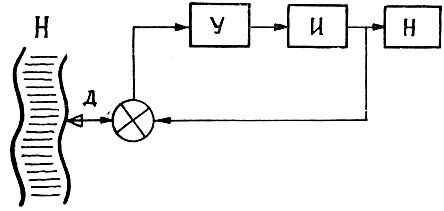
Рис. 31 Модель замкнутой системы управления

Два обстоятельства, связанные с моделью, показанной на рис. 31, позволили нам провести аналогию между замкнутой системой управления и игроком. Первая - то, что объект управления подвергается случайным внешним возмущениям и сам вследствие этого совершает действия, которые могут рассматриваться как случайные события. Именно это и дало нам возможность сравнить объект управления с противником, ходы которого нельзя в точности предсказать заранее. Второе обстоятельство - это наличие в составе системы управления элемента, определяющего стратегию управления. Сосредоточим на некоторое время наше внимание именно на этом элементе.

Отметим одну особенность предыдущего изложения, которая, возможно, ускользнула от внимания читателя. Когда речь шла об игроке, мы говорили, что он предугадывает или, во всяком случае, должен предугадывать ближайший ход противника. Перейдя к охотнику, мы стали говорить, что он рассчитывает точку встречи. То же самое относилось и к стрелку из зенитного орудия. Угадывает или рассчитывает? Что это, простая вольность слов, допущенная авторами, или в этом-то и заключается некое принципиальное различие между игроком и охотником? Но ведь мы неоднократно подчеркивали, что предполагается именно случайное поведение объекта. Если это и не совсем справедливо применительно к утке, то явно справедливо применительно к самолету, совершающему противозенитный маневр. Но тогда возникает вопрос: можно ли рассчитать заранее момент наступления случайного события или, в более общем случае, характер протекания случайного процесса^*, если по самому определению случайными мы называем такие события, моменты наступления которых нам неизвестны?

^*(Случайным процессом называется последовательность отдельных случайных событий.)

Подобный вопрос заинтересовал в свое время некоего кавалера де Мере. Это было в середине XVII века. Кавалер де Мере подобно кавалеру, грустную судьбу которого мы описали во вступлении к этой главе, также не чуждался азартных игр. Правда, в отличие от своего неудачливого коллеги он не проиграл состояние и ему не пришлось нарушать покой старой графини. Однако, будучи по своему времени образованным человеком, кавалер де Мере задумался о том, может ли игрок рассчитывать средствами математики свои шансы в игре и определять стратегию на основании такого расчета. Со своими сомнениями кавалер обратился к одному из образованнейших и талантливейших людей того времени Блезу Паскалю.

В 1653 г. со своими знатными друзьями - герцогом Роанским, кавалером де Мере и Дамьеном Митоном - Паскаль ездил в Пуату. Во время этого путешествия де Мере и задал Паскалю свои два вопроса об азартных играх. Правда, на первый из этих вопросов де Мере оказался в состоянии ответить сам. Вопросы кавалера де Мере послужили основанием для переписки между Паскалем и другим великим французским математиком Ферма. Три письма Паскаля к Ферма от 29 июля, 24 августа и 27 октября 1654 г. положили начало новой отрасли математики, названной теорией вероятностей. Значительно позже, уже в XX веке, методы теории вероятностей были положены в основу создания другой теории, названной теорией игр. Теория игр сама по себе не является вероятностной теорией, и методы теории вероятностей используются в ней как средство получения некоторых решений. Однако вернемся к началу нашего рассказа.

Размышляя над задачами кавалера де Мере, Паскаль поставил перед собой вопрос: можно ли применить к случайным событиям, т. е. к событиям, о которых, грубо говоря, мы ничего не знаем, кроме того, что каждое такое событие рано или поздно наступает, какую-либо количественную меру? Оказывается, количественной мерой случайного события может служить вероятность его наступления.

Представим себе ситуацию, которая может иметь несколько различных исходов, случайных в том смысле, что мы не знаем заранее, какой именно из этих исходов наступит. Пусть, например, подобная ситуация состоит в том, что в воздухе находится подброшенная игральная кость. Исход ситуации - падение кости на стол определенной стороной вверх. Всего у кости шесть сторон, а следовательно, у данной ситуации шесть возможных исходов. Предположим теперь, что мы подбросили кость очень много раз подряд и посчитали, сколько раз выпала единица, сколько раз двойка и так далее до шестерки. Величину m₁/n, где m₁ - количество случаев, когда выпала единица, an - общее количество бросаний кости, назовем частотой выпадания единицы. Аналогичным образом можно определить частоту выпадания двойки или других сторон кости. По мере увеличения количества бросаний частота будет стремиться к определенной величине. Эта величина и называется вероятностью.

Математически то же самое можно записать следующим образом:

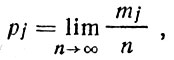
где p₁ - вероятность выпадания единицы, р₂ - вероятность выпадания двойки и так далее, р₆ - вероятность выпадания шестерки.

Если кость представляет собой куб правильной формы, то вероятности выпадания всех ее сторон окажутся равными в точности одной шестой. Вообще из самого способа определения вероятности мы можем заключить, что вероятность - это положительная величина, заведомо не большая единицы.

Продолжая бросать игральную кость, мы легко можем прийти также к выводу, что частота выпадания двух каких-либо граней, скажем, либо двойки, либо четверки, в точности равна сумме частот выпадания каждой из них в отдельности. То же самое справедливо и для вероятностей. Вероятность исхода, состоящего в том, что имеет место хотя бы один из двух каких-либо исходов, равна сумме вероятностей каждого из этих исходов в отдельности. Эта - знаменитая теорема сложения вероятностей, также открытая Паскалем, справедлива только тогда, когда ситуации несовместны, т. е. исходы каждой из них никак не зависят от исходов предыдущих ситуаций.

Паскалем была сформулирована также и другая теорема: для независимых ситуаций вероятность сложного исхода, состоящего в том, что в двух следующих друг за другом ситуациях сначала наступит исход А, а затем исход Б, равна произведению вероятностей каждого исхода в отдельности. Другими словами, вероятность того, что при двух последовательных бросаниях кости выпадут две шестерки подряд, равна 1/36. К слову сказать, это и есть ответ на первый вопрос кавалера де Мере.

Мы не намерены здесь излагать даже самые элементарные сведения из области теории вероятностей, потому что это уже с успехом сделали до нас другие авторы^*. Однако из того, что уже сказано, можно сделать выводы, которые сыграют в дальнейшем очень важную роль.

^*(Е. С. Вентцель. Теория вероятностей, М., Фнзматгиз, 1962.)

Во-первых, теория вероятностей позволяет применять к случайным событиям количественную меру. Такой мерой является вероятность наступления этих событий. Во-вторых, для определения величины вероятности требуется наблюдать достаточно большое количество исходов независимых ситуаций. Наконец, в-третьих, знание вероятности наступления события не приносит особой пользы, если рассматривается лишь одно-единственное событие данного типа.

Последний вывод не столь очевиден, как два предыдущих, поэтому обсудим его несколько подробнее. Рассмотрим одну из простейших азартных игр, состоящую в подбрасывании монетки. Пусть условия игры состоят в следующем. Один из игроков подбрасывает монетку, а другой берется угадать, на какую сторону она упадет. При правильном угадывании он получает, а при неправильном отдает определенную сумму, причем величина суммы назначается перед каждым подбрасыванием.

Если монетка имеет абсолютно правильную форму, то вероятность выпадания герба та же, что и вероятность выпадания решетки, и равна ½. Ясно, что если вся игра сводится к одному только подбрасыванию, знание вероятности выпадания герба и решетки ничего не дает ни тому, ни другому игроку.

Предположим теперь, что вся игра состоит не из одного, а из четырех независимых подбрасываний. Предположим также, что три подбрасывания уже имели место и при этом каждый раз выпадала решетка. Каковы вероятности выпадания сторон при четвертом подбрасывании? Согласно теореме умножения вероятностей вероятность того, что решетка выпадет и в четвертый раз, т. е. четыре раза подряд, равна 1/16. На основании теоремы сложения вероятностей вероятность того, что выпадет либо герб, либо решетка, равна единице. Следовательно, в рассматриваемой ситуации вероятность того, что при четвертом бросании выпадет герб, равна:

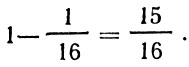
Это очень большая вероятность, и, казалось бы, у отгадывающего есть все основания поставить на герб достаточно большую сумму. Однако вряд ли все сказанное послужит ему утешением, если монета все-таки и в четвертый раз упадет решеткой кверху. А это вполне может случиться. Вспомним, что события, по определению, независимы, следовательно, у подброшенной в четвертый раз монеты ровно столько же шансов упасть вверх решеткой, сколько и гербом. Этот кажущийся парадокс на самом деле не является парадоксом, а свидетельствует лишь о необходимости хорошо разобраться в сущности самого понятия вероятности.

Подобно тому, как выше мы ввели понятие вероятности простого события, т. е. события, состоящего в наступлении одного какого-либо исхода, можно ввести понятие вероятности более сложных событий, состоящих в одновременном наступлении нескольких различных исходов. Например, запись р(А, В) означает вероятность сложного события, состоящего в том, что одновременно наступают исход А и исход В. Если бросить две игральных кости, то они одновременно упадут на стол и каждая из них ляжет вверх какой-нибудь стороной. Пусть А - это событие, состоящее в том, что первая кость упала вверх стороной А, а В - это событие, состоящее в том, что вторая кость упала вверх стороной В. Тогда запись р(А, В) будет вероятностью наступления сложного события, связанного с положениями обеих костей. Сложные события могут состоять из трех и более исходов. Вероятность сложного события определяется точно так же, как и простого, т. е. подсчитывается частота наступлений сложного события и рассматривается предельное значение этой частоты при устремлении количества испытаний к бесконечности. Если отдельные исходы, составляющие сложное событие, взаимонезависимы, то на основании теоремы умножения вероятностей будет справедливо равенство

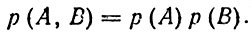
Существенное значение в приложениях теории вероятностей имеет также понятие условной вероятности. По определению, условной вероятностью р(А/В) наступления исхода А, если известно, что перед этим имел место исход В, называется величина

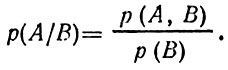
Условную вероятность необязательно вычислять по только что приведенной формуле. Ее можно получить и непосредственно из экспериментов точно так же, как мы поступали выше. Для этого нужно регистрировать все случаи, когда исход А наступает вслед за исходом В. Затем подсчитавается частота этих случаев. Сказанное свидетельствует о том, что условная вероятность суть такая же объективная мера, как и обычные вероятности простых и сложных событий.

Покажем теперь, как понятие условной вероятности позволяет разрешить отмеченный нами выше парадокс. Предположим снова, что мы подбрасываем монетку четыре раза подряд. Исход каждого подбрасывания - это независимое событие, поэтому вероятность сложного события, состоящего в том, что три раза подряд монетка выпадала решеткой вверх, согласно теореме умножения вероятностей равна 1/8 - Обозначим эту вероятность через р{В).

Вероятность сложного события, состоящего в том, что при трехкратном подбрасывании монеты каждой раз выпадала решетка и при четвертом следующем подбрасывании тоже выпадет решетка [обозначим эту вероятность через р(А, В)], согласно теореме умножения вероятностей равна:

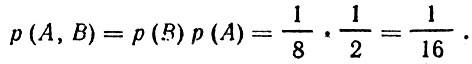
Именно эту величину мы и получили выше. Но существенное обстоятельство заключается здесь в том, что, подбрасывая монету в четвертый раз, мы знаем результаты трех предыдущих подбрасываний. Следовательно, здесь мы должны пользоваться понятием условной вероятности, т. е. определять вероятность выпадания решетки, если известно, что перед этим три раза подряд выпадала решетка. Эта вероятность равна:

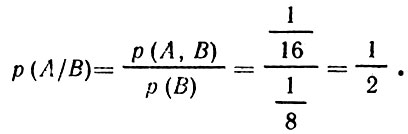
Теперь все встает на свои места. Ведь все, что происходит, когда подбрасывается в воздух монета, никак не зависит от того, подбрасывается она в первый или не в первый раз. Именно это обстоятельство и представляет собой существо утверждения о независимости исходов. Поэтому когда мы бросаем монету и при этом не знаем, имели ли место предыдущие подбрасывания, мы с полным основанием можем считать, что монетка подбрасывается впервые, и пользоваться понятием вероятности простого события. Если же мы знаем результаты предыдущих испытаний, то надо пользоваться условной вероятностью. Как было только что показано, результат в обоих случаях один и тот же.

Приведем еще более разительный пример. Пусть имеется колода, состоящая из шестнадцати карт: четыре туза, четыре короля, четыре дамы и четыре валета четырех различных мастей. Посчитаем, какова вероятность того, что после перетасовки колоды карты окажутся сложенными в любом заданном порядке. Карта, лежащая сверху, может быть любой из шестнадцати. Следовательно, вероятность того, что сверху окажется, например, туз пик, равна 1/16 - Второй по порядку может оказаться любая из оставшихся пятнадцати карт, и вероятность для любой из них оказаться в этом положении равна 1/15 - Продолжая подобные рассуждения, приходим к выводу, что вероятность картам оказаться сложенными в данном порядке равна:

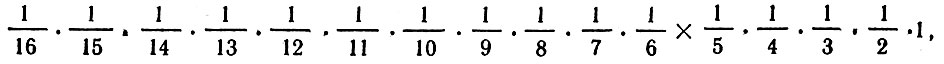
что примерно составляет 0,00000000000005. Это исчезающе малая величина, и все же после каждой перетасовки колоды карты оказываются сложенными в некотором определенном порядке, т. е. осуществляется событие, имеющее столь малую вероятность наступления. Более того, оно происходит каждый раз после очередной перетасовки карт.

К какому же выводу приводят нас эти примеры? Для игрока в азартные игры вывод очевиден - не надо ставить на карту все, даже когда вероятность выигрыша очень велика. Лучше всего вообще не играть в азартные игры. С другой стороны, по тем же самым соображениям имеет прямой смысл покупать лотерейные билеты. Ведь как бы ни мала была вероятность выиграть, например, автомобиль, такой выигрыш выпадает в каждом розыгрыше и у купившего билет ничуть не меньше шансов получить этот выигрыш, чем любого другого, также купившего один билет.

Иначе оборачивается дело, когда рассматривается не одно случайное событие, а последовательность большого количества таких событий - случайный процесс. Вспомним, что с самого начала мы определили вероятность как предел, к которому стремится частота исходов при условии, что количество независимых ситуаций, порождающих эти исходы, неограниченно растет. Отсюда можно сделать заключение, что вероятность представляет собой некую меру частоты исходов.

Поясним сказанное еще на одном примере. Пусть снова двое играют, подбрасывая монету, причем на этот раз ставка при каждом подбрасывании остается неизменной. Чем больше было количество подбрасываний, тем ближе будет частота выпаданий, например, герба к ½. Следовательно, если стратегия отгадывающего состоит в том, чтобы каждый раз загадывать герб, то с увеличением количестра подбрасываний вероятность окончания игры вничью увеличивается и при бесконечном количестве подбрасываний вероятность превратится в достоверность.

Этот последний пример дает нам уже определенную идею о том, как используются методы теории вероятностей при разработке стратегий и, в частности, стратегии управления. Заметим попутно, что если игроки пользуются правильной монеткой, то не существует стратегии, которая приводила бы одну из сторон к выигрышу при достаточно большом количестве подбрасываний.

Но цель, которая стоит перед игроком, называемым системой автоматического (или не автоматического) управления, состоит именно в том, чтобы получить выигрыш. Наш краткий экскурс в область теории вероятностей пока позволил сделать в этом плане лишь пессимистические выводы. Но не будем отчаиваться. Дело в том, что в природе очень редко встречаются абсолютно правильные игральные кости или монеты. Именно это обстоятельство и позволяет в подавляющем большинстве случаев верно построить стратегию игры и получить желаемый выигрыш. Более подробно мы рассмотрим этот вопрос позднее, а пока ограничимся лишь указанием на следующее.

В состав системы автоматического управления замкнутого типа входит элемент, занимающийся разработкой стратегии управления. Согласно всему сказанному ранее этот элемент должен решать по меньшей мере две самостоятельные задачи: определять вероятности наступления тех или иных событий и на основании знания этих вероятностей разрабатывать стратегию управления.

Теперь мы можем вернуться к тому, что побудило нас обсуждать поведение кавалера де Мере, а также последствия, вызванные его любознательностью к различию понятий "угадать" и "рассчитать". Мы уже знаем, что предугадать наступление того или иного события можно, рассчитав его вероятность/При этом остается в силе все сказанное по поводу одиночных событий. Система управления, работающая по принципу расчета-предугадывания, никогда не может гарантировать того, что наступление каждого отдельного события будет предугадано правильно. Однако частота правильных отгадываний может быть достаточно высокой.

Вернемся еще раз к вопросу о различии между разомкнутой и замкнутой системами. Мы неоднократно отмечали то обстоятельство, что обратная связь в замкнутой системе вступает в действие, т. е. система по-настоящему оказывается замкнутой лишь тогда, когда значения регулируемого параметра отклоняются от значений, предписанных программой. В общем случае и при отсутствии таких отклонений система может выполнять достаточно сложные действия. Поскольку при отсутствии отклонений обратная связь не работает и ее можно исключить из рассмотрения, в промежутках между отклонениями замкнутая система работает, как разомкнутая. Иными словами, разомкнутая система представляет собой как бы частный случай замкнутой системы.

Разовьем эту мысль еще дальше. Истинной стратегией игры против внешних возмущений является последовательность управляющих воздействий, поступающих в нашей модели (см. рис. 31) на вход усилителя. Однако часть этой модели, состоящая из усилителя, исполнительного механизма и объекта, ничем не отличается от усилителя, исполнительного механизма и объекта в модели разомкнутого типа системы, показанной на рис. 30.

Это позволяет нам рассматривать программу, записанную на носителе в разомкнутой системе управления, как стратегию управления. Можно рассуждать и с противоположных позиций. Стратегия управления в системе управления замкнутого типа состоит как бы из двух частей, одна из которых задана заранее и зафиксирована на носителе, а другая формируется в процессе управления в ответ на воздействие внешней среды. Например, при игре в шахматы первая часть стратегии содержит правила ходов различными фигурами, а также некоторые неизменные правила разыгрывания дебютов и эндшпилей. Вторая часть строится игроком в зависимости от поведения противника.

Заметим в заключение, что в достаточно большом числе реальных ситуаций поведение внешней среды может быть предсказано, во всяком случае принципиально, на достаточно большое время вперед. Следовательно, существует принципиальная возможность обходиться в этих случаях системами разомкнутого типа, задавая им, однако, чрезвычайно сложные программы. Но на практике так обычно не поступают именно из-за сложности программ.

Хорошим примером служит система управления уличным освещением городов. Моменты наступления темноты можно предсказать наперед на сколь угодно долгое время. Поэтому управлять включением и выключением уличного освещения в принципе можно было бы с помощью сложного часового механизма, отсчитывающего не только время суток, но и время года, Но ведь гораздо проще заменить этот часовой механизм одним-единственным фотоэлементом, который действительно выдает сигнал в тот момент, когда освещенность его падает ниже заданного уровня.

Именно так и поступают на практике. Разомкнутые системы управления оказываются целесобразными лишь тогда, когда стратегия управления достаточно проста. Во всех прочих случаях используются замкнутые системы. По этой причине и мы на страницах нашей книги распрощаемся с разомкнутыми системами. Заодно, как это ни тяжело, мы распрощаемся с лягушками и автомобилями, с мамонтами и мылом. Все они были нужны нам только для того, чтобы сформулировать некоторые основные принципы кибернетики и показать, что эти принципы остаются неизменными как в живых, естественных системах, так и в искусственно создаваемых устройствах. Подобная неизменность привела нас к понятию модели. Дальнейшее рассмотрение мы поведем лишь применительно к моделям, ни на минуту не забывая, однако, что эти модели суть лишь описание определенных свойств, в равной степени присущих и мамонтам, и автомобилям, и лягушкам, и даже мылу.