На берегах древнего Нила

На сотни и сотни километров узкой лентой растянулась Нильская долина. По обе ее стороны раскинулись зыбкие пески. Нет им края. Они угрожающе надвигаются на Египет и, кажется, готовы похоронить под собою и Нил и людей, с незапамятных времен обосновавшихся на его берегах. Но спокойно несет свои воды могучая река, не боится она страшных песков, и жизнь на ее берегах не прекращается ни на минуту.

Ежегодно в начале июня кроваво-красные потоки стремительно мчатся со снежных вершин далеких Абиссинских гор. Набухает Нил, выходит из берегов, наводнение быстро распространяется с юга на север, и через две-три недели весь Египет оказывается покрытым водой.

Но это не стихийные бедствия. Разливы Нила обильно удобряют и щедро орошают землю египтян, и без животворной нильской воды палящие лучи солнца погубили бы посевы земледельцев.

Четыре месяца в году владеет Египтом Нил, и когда он входит в свои берега, почва долины глубоко напитана водой, обогащена жирным илом. Так река готовит землю к вспашке и посеву.

После разлива владельцы возвращались на свои участки и очень часто не могли установить их границы. Это приводило к кровавым распрям из-за узких драгоценных полосок земли.

И вот здесь-то, на берегах древнего Нила, и зародились точные методы измерения - способы вычисления площадей земельных участков. Отсюда около четырех тысяч лет назад началось развитие арифметики, алгебры и геометрии.

В те времена границы Египта доходили до отрогов Тавра и реки Евфрата. Египтяне поддерживали оживленную торговлю с соседними и отдаленными государствами.

Вся страна была измерена и разделена на округа - номы. Ежегодно производились обмеры земельных участков и перепись "быков и мелкого скота". Все, что делали тысячи невольников, тщательно подсчитывалось надсмотрщиками-счетоводами.

Армии рабов строили гигантские сооружения - пирамиды. Они расположены с такой точностью по отношению к сторонам света, которая может быть достигнута только, когда архитектор и астроном работают рука об руку. Точные пропорции сооружений свидетельствуют о выдающихся геометрических познаниях их.творцов.

В глубоких тайниках пирамид, усыпальниц египетских царей и жрецов, среди богатой золотой утвари и драгоценностей искатели древних кладов находили свернутые в трубки темно-коричневые свитки - папирусы, исписанные причудливыми иероглифами. Почти две тысячи лет ученые разных стран пытались проникнуть в тайны египетской письменности. Надо было заставить мертвые листки рассказать об истории и культуре древнего Египта.

Когда это удалось сделать, ученые узнали и о математике древних египтян. Среди многочисленных папирусов нашли около пятидесяти математических документов. Самый древний памятник египетской математики, так называемый "Московский папирус", - документ XIX века до нашей эры. Он был приобретен в 1893 году собирателем древних сокровищ Голенищевым, а в 1912 году перешел в собственность Московского музея изящных искусств.

Самый большой математический документ - папирус по руководству к вычислениям писца Ахмеса - найден в 1858 году английским коллекционером Райндом. Папирус составлен в XVII веке до нашей эры. Его длина 20 метров, ширина 30 сантиметров. Он содержит 80 различных арифметических, алгебраических и геометрических задач с решениями.

Вот примерное изложение одной из задач этого папируса.

"Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками; разница между каждым человеком и его соседом составляет - 1/8 меры. Средняя доля есть одна мера. Вычти одну из 10; остаток 9. Составь половину разницы; это есть 1/16. Возьми ее 9 раз. Приложи это к средней доле; вычитай для каждого лица по 1/8 меры, пока не достигнешь конца".

Здесь, на берегах древнего Нила, и зародились точные методы измерения земли

Затем приводятся все десять долей:

25/16, 23/16, 21/16, 19/16, 17/16, 15/16, 13/16, 11/16, 9/16, 7/16, и результат проверяется сложением.

Математический документ древнего Египта не научный трактат по математике, а практический учебник с примерами, взятыми из жизни.

Среди задач, которые должен был решать ученик школы писцов, - вычисления и вместимости амбаров, и объема корзины, и площади поля, и раздела имущества среди наследников, и другие. Писец должен был запомнить эти образцы и уметь быстро применять их для расчетов.

'Московский папирус' - древнейший памятник египетской математики

"Не допусти, - говорится в одном из наставлений писцам, - чтобы о тебе сказали, что есть такие вещи, которых ты не знаешь".

В древнем Египте пользовались только простейшими дробями, у которых числитель равен единице. Для каждой такой дроби, например 1/2, 1/4, 1/8 и так далее, был свои иероглиф. Всякую другую дробь, например 9/16, они представляли как сумму 1/2+1/16; 7/8=1/2+1/4+1/8 и так далее.

Это записывалось так: /2 /16; /2 /4 /8.

Проводить различные вычисления, выражая все дроби через простейшие, было, конечно, очень трудно и отнимало много времени. Поэтому египетские ученые позаботились об облегчении труда писца. Они составили специальные таблицы разложений дробей на простейшие. В папирусе Райнда приведена такая таблица для дробей с числителем, равным 2. По ней можно сразу найти простейшие дроби, полученные при делении 2 на различные числа.

По математическим папирусам ученые установили, что египетские математики умели возводить в степень, знали начала алгебры и даже решали уравнения с двумя неизвестными. Немалого достигли египтяне и в геометрии. Они умели вычислять площадь круга, принимая отношение его периметра к диаметру равным 3, площадь треугольника, объемы цилиндра и усеченной пирамиды, поверхность полушария и решали многие другие, сложные для своего времени задачи.

Почти одновременно с зарождением математики в Египте возникла и вавилонская математика.

Жители древнего Вавилона писали клиновидными знаками на глиняных плитках. После сушки они приобретали большую прочность.

За последние тридцать лет найдено много вавилонских математических памятников. По ним удалось создать представление о математических знаниях древних.

Вавилоняне очень много занимались астрономией - самой древней из всех наук. Ее зарождение относится к тем отдаленным временам, когда начинается история человечества.

Много тысячелетий тому назад люди обращали взоры к небосводу. Постоянная смена дня и ночи, изменение положения солнца на небе не могли не привлекать внимания человека. Люди пытались разгадать тайны неба, накапливали различные факты и искали закономерности небесных явлений.

Чтобы измерять время и ориентироваться по небесным светилам, вавилоняне вели обширные наблюдения над звездами, изучали их расположение и производили в связи с этим большие вычисления. Так были заложены основы астрономической науки.

При дворе вавилонских и ассирийских царей постоянно содержался обширный штат звездочетов-астрологов. Собирая полезные для развития астрономии факты, они вместе с тем уделяли большое внимание астрологии - лженауке об определении будущего по светилам.

Ни одно важное государственное дело, ни один военный поход древние цари не предпринимали без совета с астрологами. По расположению звезд астрологи вычисляли благоприятные сроки походов или других важных для страны или царя событий.

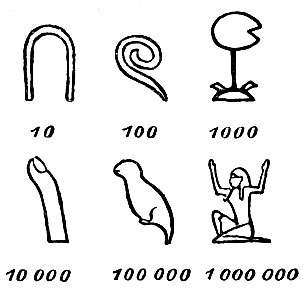
Такими иероглифами египтяне изображали числа

Вот как халдейский прорицатель Белезис предрекал по звездам судьбу Ассирии в байроновокой трагедии "Сарданапал":

 Окончен день; мне кажется, что солнце
 Медлительней заходит, точно жаль
 Ему ..навек с Ассирией расстаться.
 В какой зловещий пурпур облеклись
 Его лучи средь этих туч суровых!
 То крови цвет, которую они
 Вещают нам! О солнце, ты, на отдых
 Идущее, вы, звезды, в небесах
 Витающие, - когда не бесполезно
 Я наблюдал движенье ваших тел,
 У вас в лучах читая приговоры,
 Столь страшные, что время, видя, с чем
 Оно идет к народам, трепетало
 За их судьбу; когда вы правду мне
 Поведали - последние минуты
 Ассирии пробили...

Астрономы и астрологи древнего Востока научились сопровождать свои наблюдения необходимыми вычислениями. Это они ввели семидневную неделю, деление круга на 360 градусов, деление часа на 60 минут, а минуты - на 60 секунд и секунды - на 60 терций. Год считали равным 360 дням. Как видите, отдавалось явное предпочтение числу 60. Оно делится на многие небольшие числа - 2, 3, 4, 5, 6, а это очень облегчало деление, доставлявшее, по-видимому, много неприятностей вычислителям.

На древних вавилонских плитках найдены различные вычислительные таблицы: квадратов чисел до 602 и кубов чисел до 323, таблицы умножения и таблицы обратных чисел для замены деления умножением.

С их помощью решали некоторые квадратные и даже кубические уравнения.

Египетские таблицы дробей и различные вавилонские таблицы - древнейшие из известных нам средств, облегчающих вычисления.

Жители древнего Вавилона писали клиновидными знаками на глиняных плитках

Велик вклад и индийцев в сокровищницу математических знаний. Они изобрели позиционный способ записи чисел только десятью знаками, которые мы обозначаем цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Любое большое число можно изобразить с помощью этих символов. При этом одна и та же цифра может иметь различные значения в зависимости от места (позиции), которое она занимает в числе. Мы теперь пользуемся десятичной системой. В ней одна и та же цифра обозначает или единицы, или десятки, или сотни, или тысячи и так далее, в зависимости от места, где она стоит в числе.

Прогрессивность позиционной системы видна хотя бы из таких примеров. В древние времена до распространения индийской системы египтяне, греки, римляне, славяне, а позднее и другие народы запись числа производили исключительно по принципу сложения и вычитания. Например, в римской нумерации число DCCLXIV обозначает "пятьсот+сто+сто+пятьдесят+десять+пять-один", то есть 764.

Я наблюдал движенье ваших тел, У вас в лучах читая приговоры...

Попробуйте при такой записи сложить какие-либо два числа или перемножить их. Вам сразу станут понятными огромные трудности, которые возникали при операциях с ними.

К тому же по мере увеличения чисел надо было выдумывать для них все новые и новые символы. Поэтому разные народы искали разные способы изображения чисел.

Греки пользовались буквами, снабженными особыми значками.

Таким же способом писали цифры наши предки, приспосабливая для этого буквы славянского алфавита. Над ними ставился особый значок - титло. Славяне пользовались двумя системами счета: "малым счетом" и "великим счетом". Первый доходил до числа 10 000 - "тьма", то есть темное число, которое нельзя себе ясно представить. Такой "малый счет" удовлетворял в те времена требованиям хозяйственной жизни. Наряду с этим употреблялся "великий счет" или "великое славянское число". В нем имелись более высокие разряды: 10⁸ - "тьма тем", 10¹² - "легеон", 10²⁴ - "леодр", 10⁴⁸ - "ворон", 10⁴⁹ - "клода". В старинных рукописях указывается, что "того числа несть больше".

Здесь показано, как разные народы написали бы число 1957

При подобной записи чисел вычисление было доступно только специалистам-профессионалам.

В народе пользовались более простым способом счета. Числа обозначали зарубками на палочках. Русские называли эти палочки бирками.

Малограмотное население разных стран записывало таким способом долговые обязательства и налоги. На палочке делали нарезы, соответствующие сумме долга или налога. Затем ее раскалывали пополам: одну половину оставляли у должника, другую хранили у заимодавца или в казначействе. Когда наступала расплата, обе половинки проверяли, прикладывая их друг к другу.

В Англии этот способ записи налогов сохранился до конца XVII века. Интересно, что когда ликвидировали старые налоговые обязательства крестьян, на дворе лондонского казначейства устроили костер из накопившихся бирок. Он был так велик, что заодно с бирками сгорело и казначейство.

Индийскую систему счета завезли в Европу итальянские купцы. Они заимствовали ее у арабов. Поэтому цифры, которыми теперь пользуются во всем мире, называют арабскими. Слово "цифра" происходит от арабского слова "цифр", что означает "пустое" (пустое место). Индийцы "пустым" называли отсутствие разряда в числе. До XVIII века наш нуль назывался "цифрой". Теперешнее название "нуль" происходит от латинского слова "nullus" - "никакая".

Когда в XIII столетии индийский принцип счета появился в Европе, он встретил сильное противодействие сторонников римской нумерации. Индийские цифры и способ записи чисел были для большинства людей вначале непонятными. Их считали какими-то тайными знаками, шифром. Слово "шифр" ггакже произошло от слова "цифр".

Начертание индийских цифр за многие столетия претерпело большие изменения. Современный их вид установился с открытием книгопечатания.

Существует много теорий для объяснения нынешней формы цифр. Некоторые пытались связать ее с числом палочек, точек, углов в цифре, но такие объяснения научного значения не имеют.

Великий Пушкин тоже занимался изучением арабских цифр. У него есть заметка с чертежом, в которой он лишен "Форма шифров арабских составлена из следующей фигуры: АД (1), АВДС (2), АВЕСД (3)".

...Обозначив углы квадрата и его центр соответствующими буквами, найдите форму последующих цифр.

Изобретение индийцами позиционной записи чисел имело огромные последствия для человеческой культуры и особенно для растущей техники вычисления. Если старинные методы счета были доступны лишь немногим, то теперь техникой счета легко овладевал каждый человек еще в детском возрасте. Кроме того, новый принцип счета облегчил создание вычислительных машин.