Рождение науки

Шумны и оживленны центральные районы Александрии, одного из древнейших городов современного Египта. В часы, когда нестерпимый полуденный зной сменяется вечерней прохладой и свежий морской воздух начинает овевать уставший город, люди разных национальностей, говорящие на разных языках мира, заполняют его улицы.

Великий Пушкин тоже занимался изучением формы арабских цифр

Многоэтажные современные здания, причудливые старинные восточные постройки, обилие зелени, море - все это придает городу необычайный облик.

Молчаливые свидетели исторических событий, многочисленные памятники, напоминают о долгой-долгой жизни города-колыбели науки и культуры.

Астрономы древнего Вавилона ввели деление круга на 360 градусов, часа - на 60 минут, минуты - на 60 секунд

Более двух тысяч лет существует Александрия. Город неоднократно переживал расцвет и упадок. Его разрушали орды завоевателей. Но проходили годы, и, словно сказочная птица Феникс, вставала Александрия из пепла.

Там, где сейчас самый оживленный район города, две тысячи лет назад шумели воды узкого пролива. Он отделял от материка небольшой остров Фарос, на котором возвышалось восьмиэтажное здание с гигантской башней, суживающейся кверху. Ее поддерживали восемь колонн. Это всемирно известный Фаросский маяк.

Яркий костер из смолистых деревьев - "фонарь" маяка- горел на вершине башни. Свет маяка отбрасывали вдаль большие зеркала. Он был виден за 50-60 километров и указывал судам дорогу в Александрийский порт.

На противоположной стороне пролива находилась богатейшая Александрийская библиотека, в книгохранилищах которой в I веке до нашей эры насчитывалось более 700 тысяч свитков. Они были собраны со всех стран древнего мира.

Здесь и в специальном музее для научных занятий были созданы прекрасные условия для работы ученых Александрийской школы. В этих стенах создавал свои бессмертные "Начала" один из величайших математиков древности - Эвклид. Его имя известно каждому школьнику. Но, к сожалению, о жизни его мы ничего не знаем. Мы даже не знаем, когда он родился и умер. Известно лишь, что жил он в III веке до нашей эры.

"Начала" Эвклида обобщают труды его предшественников - Пифагора, Евдокса и других математиков. Эта замечательная книга составляет основу классической геометрии и является блестящим примером стройной логической системы доказательств.

С какой поразительной, подчас даже грозной для невнимательного школьника последовательностью в ней из аксиом вытекают теоремы, из теорем -следствия! Ведь стоит здесь потерять хотя бы одно звено в цепочке логических рассуждений, и дорога к доказательству теоремы закрыта.

Конечно, каждый прекрасно понимает, что к правильным выводам можно прийти путем верных логических рассуждений. Когда мы утверждаем:

"Все вписанные углы, опирающиеся на диаметр, - прямые;

данный вписанный угол опирается на диаметр;

следовательно, данный вписанный угол - прямой",

то мы на основе этих рассуждений приходим к правильному умозаключению.

А как доказать, что правильная на первый взгляд цепочка рассуждений:

"Все треугольники суть замкнутые геометрические фигуры";

"семиконечная звезда также замкнутая геометрическая фигура";

"следовательно, семиконечная звезда - треугольник",

приводит к явно неверным выводам, то есть содержит где-то логическую ошибку?

Какие закономерности управляют системой логических рассуждений? Можно ли их изучить, можно ли раскрыть неумолимые законы логического мышления?

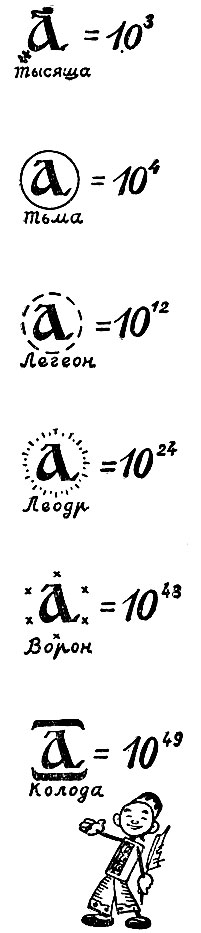
'Малый' и 'великий' счет у древних славян

Такие вопросы давно интересовали ученых. Многие философы и ученые древнего Китая, Индии, а также древней Греции пытались на них ответить.

Тесное общение философов с математиками в период зарождения математической науки способствовало также развитию логики.

Логика - это наука о формах и законах мышления человека.

Основы логики были изложены современником Эвклида греческим философом Аристотелем. Его последователи объединили логические сочинения Аристотеля под общим названием "Органон" - орудие (знания). Многое из того, что было сделано великим философом, сохранилось и в современном учении о логике.

Логика рассматривает три различные формы, в которых осуществляется процесс мышления: понятие, суждение и умозаключение.

"Этот вписанный угол, опирающийся на диаметр", - это есть понятие; если мы здесь говорим не о всех углах - то понятие единичное. А "все вписанные углы, опирающиеся на диаметр, - прямые" - уже является суждением, поскольку в нем имеется объект суждения и указаны свойства объекта.

Если из двух суждений выводится третье, то основными формами таких умозаключений являются умозаключения, которые в логике называют силлогизмами. В силлогизме одно из суждений рассматривается как большая посылка, другое суждение - как малая посылка и третье, заключительное суждение - как вывод.

Возьмем суждение "все вычислительные машины облегчают труд человека" в качестве большой посылки. А "арифмометр - вычислительная машина" - в качестве малой посылки. Тогда вывод из этих суждений предстанет в таком виде: "арифмометр облегчает труд человека".

Суждения могут быть истинные или ложные. Если суждения истинные, то при соблюдении определенных законов образования силлогизма мы всегда получим правильный вывод - истинное заключительное суждение.

Такими являются наши суждения и вывод об арифмометре.

Но если при соблюдении правил образования силлогизма мы получаем неверный, ложный вывод, то это значит, что по крайней мере одна из посылок ложна.

Наоборот, если все посылки были истинными суждениями, но в результате умозаключения получен ложный вывод, то это означает - нарушено какое-либо правило образования силлогизма.

Нелепый вывод - семиконечная звезда - треугольник - получился у нас из-за неправильного построения силлогизма. Хотя посылки были верны.

Как часто в жизни мы встречаем такие случаи! Кажется, правильно рассуждает человек, а сделает вывод - нелепость.

Некий гражданин обижен соседом. Он знает, что "все соседи люди". Но "его сосед грубиян". Это, может быть, и верно. И вот нелепый вывод: "все люди грубияны".

Это типичное нарушение правила силлогизма.

Законы логики, сформулированные Аристотелем, носят формальный характер, поэтому аристотелевская логика и называется формальной. Она, конечно, недостаточна для полного научного исследования.

Могучим орудием человеческого познания мира является диалектическая логика, для которой формальная логика есть низшая ступень, или, как говорил Энгельс, "низшая математика" логики. Диалектическая логика наиболее полно отражает объективно существующую действительность, отражает наиболее существенные связи и отношения предметов, явлений.

Однако марксизм не только не отрицает необходимость формальной логики, очищенной, конечно, от идеалистических и схоластических извращений, но подчеркивает большое значение формальной логики в процессе выработки элементарных правил научного мышления. Формальная логика учит мыслить правильно, соблюдая однозначность мысли, непротиворечивость мысли, ее определенность, доказательность и последовательность.

Логические закономерности, установленные Аристотелем, способствовали созданию стройной системы математических взглядов. Ведь математические знания египтян, вавилонян, индийцев составляли лишь отдельные практические приемы решения различных арифметических, алгебраических и геометрических задач. Греческие, в частности александрийские, математики тщательно систематизировали и развили эти знания на основе строгих логических доказательств. Так были заложены основы математической науки.

Вместе с тем многие выдающиеся математики пытались и самим логическим построениям придать более точную форму, прибегнув к помощи специального математического аппарата - математической логики. Но лишь в XIX веке, почти через две тысячи лет после рождения науки о логике, удалось достигнуть успеха В решении этой проблемы.

Математическая логика нашла широкое применение в современных вычислительных машинах. Более подробно мы еще с нею познакомимся, а теперь вернемся к рассказу о древнегреческих математиках.

Сношения между греческими колониями, разбросанными в разных концах мира, помогли распространению математических знаний во многих странах. Труды греческих ученых возбудили интерес к методам строгого обоснования математических исследований,

К сожалению, сам Эвклид и некоторые другие его современники, а также их ученики и последователи в Греции пренебрежительно относились к практическим применениям математики. Для большинства из них занятия математикой превратились в средство тренировки ума, в своеобразные изощренные логические рассуждения и споры. Все, что было связано с конкретным числовым приложением, с вычислительной математикой, отвергалось как нечто ненаучное, второстепенное.

Такое отношение к требованиям жизни привело к печальным последствиям. В начале нашей эры развитие греческой математики, и в частности геометрии, приостановилось.

В это время господствующее положение на мировой арене заняло Римское государство. Длительные войны, которые вел Рим для завоевания Греции, и захват римлянами Александрии привели математическую науку к упадку. Право на жизнь сохранили лишь области математики, нашедшие приложение в астрономии.

Греческие астрономы использовали математические методы для изучения законов, управляющих небесными явлениями. В связи с этим они много сделали для развития вычислительной математики.

Труды греческих астрономов завершаются исследованиями знаменитого александрийского математика и астронома Клавдия Птолемея. Он жил в первой половине II века нашей эры и оставил после себя сочинение в 13 томах под названием "Великое собрание", или "Великое построение". Это была как бы энциклопедия астрономических знаний того времени.

До нас она дошла только в арабском переводе под названием "Альмагест".

В "Альмагесте" приведены результаты огромной вычислительной работы, проделанной Птолемеем. Они представлены в виде таблиц синусов и предназначались для облегчения вычислительного труда астрономов.

По таблицам можно определить синусы дуг до 90 градусов через каждую 1/4 градуса, а по теореме Пифагора - вычислять любой элемент (сторону или угол) плоского прямоугольного треугольника, два других элемента которого известны.

Таблица Птолемея - первая из дошедших до нас тригонометрических таблиц.

Длительный период римского господства в Европе не отмечен какими-либо выдающимися достижениями в математике. Только александрийский ученый Диофант, живший в III веке нашей эры, внес в алгебру новое - своеобразные алгебраические уравнения.

Диофант много лет своей жизни посвятил уравнениям и, умерев, не расстался с ними. На его гробнице сделана интересная надпись. Чтобы полностью понять ее смысл, надо решить математическую задачу. Попробуйте и вы сделать это. Тогда узнаете некоторые подробности жизни замечательного древнего математика.

Вот эта надпись:

 "Путник! Здесь прах погребен
 Диофанта. И числа поведать 
 Могут, о чудо, сколь долог 
 был век его жизни.
 Часть шестую его представляло 
 прекрасное детство,
 Двенадцатая часть протекла 
 еще жизни - покрылся
 Пухом тогда подбородок.
 Седьмую в бездетном 
 браке провел Диофант.
 Прошло пятилетие; он
 Был осчастливлен рожденьем 
 прекрасного первенца сына,
 Коему рок половину лишь 
 жизни прекрасной и светлой
 Дал на земле по сравнению с отцом.
 И в печали глубокой
 Старец земного удела конец 
 воспринял, переживши
 Года четыре с тех пор, как 
 сына лишился.
 Скажи, сколько лет жизни достигнув,
 Смерть воспринял Диофант?"

Решив столь оригинальное уравнение, вы узнаете, что "прекрасное детство" длилось у Диофанта 14 лет, через 7 лет - в 21 год - он женился, в 38 лет у него появился первенец сын, на 80-м году жизни у математика умер сын, а в 84 года скончался и сам Диофант.

Алгебраические уравнения, известные под названием диофантовых, отличаются тем, что их решение должно быть дано в целых числах. Вот один из примеров, который приводит к необходимости решения таких уравнений.

"Требуется на пять рублей купить 20 штук почтовых марок: сорокакопеечных, двадцатикопеечных и пятикопеечных. Сколько окажется марок каждого достоинства?"

Для решения задачи можно, очевидно, составить два уравнения с тремя неизвестными:

40х+25у+5z=500

где х - число сорокакопеечных марок, у - двадцатипятикопеечных и z - пятикопеечных.

Хотя два уравнения с тремя неизвестными имеет бесчисленное множество решений, но отнюдь не очевидно, что среди них найдется хотя бы одно с целыми и положительными х, у и z.

Для нашей задачи можно, оказывается, найти два таких решения:

1-е решение:

x=4

у=13

z=3

2-е решение:

х=8

у=6

z=6

Проверкой можно легко установить правильность обоих решений.

Диофантовы уравнения по сей день вызывают особый интерес математиков в связи с тем, что до сих пор не удалось найти общих правил для их решения. Они и для нас представляют интерес. Почему? Об этом мы расскажем в следующей главе,