Таблицы, удвоившие жизнь астрономов
В зрительном зале погас свет. На сцену, ярко освещенную огнями рампы, вышел человек в строгом черном костюме - не цирковой артист, не конферансье, развлекающий публику, и не исполнитель веселых песенок. У него в руках мел и тряпка. Они как-то непривычны на большой и нарядной сцене.
Эстрадный номер начинается. Сотни зрителей с неослабевающим вниманием следят за исполнителем. Что же здесь происходит?
Выступает артист - "живой арифмометр". Виртуоз-вычислитель демонстрирует искусство молниеносного счета.
- Назовите мне, пожалуйста, - обращается он к зрителям,- многозначное множимое и многозначный множитель, и прошу вас найти вместе со мною их произведение.
- Один миллион пятьсот девяносто четыре тысячи триста двадцать три умножьте на три тысячи четыреста пятьдесят шесть, - несется из зала.
Проходит несколько секунд, и все читают на доске результат: 5 509 980 288.
Артист терпеливо ждет, пока зрители перемножат на бумаге числа. После этого он называет также все промежуточные результаты, полученные при умножении.
Но вот встает один из зрителей и с трудно скрываемым недоверием обращается к артисту:
- Скажите, пожалуйста, не могли бы вы, хотя бы в целых числах, извлечь корень четырнадцатой степени из семизначного числа, например из четырех миллионов семисот восьмидесяти трех тысяч восьмиста шестидесяти девяти.
И не успел зритель назвать последнюю цифру, как со сцены прозвучал ответ:
- Пожалуйста, корень четырнадцатой степени из вашего числа равен трем.
Недоверчивый зритель изумлен.
Между тем как раз решение этой на первый взгляд такой сложной задачи не представляет для вычислителя особой трудности.
Виртуоз-вычислитель, конечно, обладает большими способностями и прекрасной памятью. Путем длительной тренировки он развил в себе умение быстро оперировать большими числами. Но только ли в этом секрет молниеносного счета? Конечно, нет!
У каждого выступающего перед публикой вычислителя есть в арсенале различные специальные приемы счета.
Правда, известны случаи столь необычайного проникновения человека в таинственный мир чисел, что даже невозможно уловить техники вычислений.
Некогда в Париже наделал много шума молодой пьемон-тец Яков Иноди. Он производил разнообразные математические вычисления и даже извлечение корней с необыкновенной быстротой.
Иноди обладал поразительной памятью, основанной на удержании звуковых впечатлений. Слух его запоминал произнесенные цифры.
Иноди объяснил свою способность тем, что, как бы слыша числа повторяемыми собственным голосом, он воспроизводил их в своей памяти. Это повторение продолжалось значительную часть дня. "Если через час или два, - говорил Иноди исследовавшей его комиссии, - я подумаю о только что названном числе, я могу повторить его с такой же точностью, как сделал это сейчас перед комиссией".
Но далеко не все обладают такими своеобразными способностями, поэтому в повседневной вычислительной работе люди пользуются разными средствами ускоренного счета. Среди них немаловажное значение имеют таблицы логарифмов.
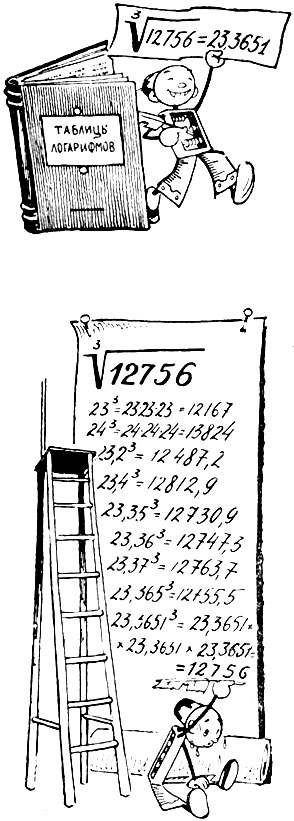
Попытайтесь вычислить сами без таблицы логарифмов корень пятой степени из того семизначного числа, которое называл зритель. Заметьте при этом время, затраченное на решение задачи.
Так как правил непосредственного извлечения корней высоких степеней не существует, то вам придется долго проделывать однообразные утомительные вычисления. Только после многих проб, может быть, удастся подобрать искомое число. А с помощью логарифмов результат получается за одну-две минуты.

Прошло всего несколько секунд, и виртуоз-вычислит ель пишет результат
Чтобы решать задачи по извлечению корней подобно виртуозу-вычислителю, нужно иметь совсем небольшую таблицу логарифмов. Многие профессионалы-вычислители запоминают ее наизусть.
Изобретение логарифмов сыграло огромную роль в развитии техники вычисления. Оно повлияло на всю методику решения математических задач. Нам, привыкшим со школьной скамьи пользоваться таблицами логарифмов, трудно даже представить себе изумление и восхищение, которое вызвало их появление.
Великий учейый Лаплас писал: "Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов".
Он говорил об астрономах потому, что в те времена им приходилось выполнять наиболее сложные и утомительные вычисления.
Это был период возрождения в Европе математической науки. До этого европейские ученые занимались главным образом освоением научного наследства греков, индийцев и арабов. Постепенно математики изучили их труды и начали вести самостоятельные исследования.
Пробуждению науки способствовала ликвидация исключительного права церковников на "ученость", а также изобретение книгопечатания, которое облегчило связь между учеными.
Новый толчок развитию математики и техники вычисления снова дала астрономия. Она должна была обслуживать мореплавателей, предпринимавших многочисленные дальние и даже кругосветные путешествия.
Гениальный астроном Коперник в те времена разработал новую теорию строения солнечной системы - гелиоцентрическую.
Другой ученый - великий математик и астроном Кеплер - сделал выдающиеся открытия в теории движения небесных тел. Астрономия соединилась с математикой и стала подлинно научной. Это требовало не только многих лет наблюдений, но и огромной вычислительной работы.
И Коперник и Кеплер прекрасно владели техникой вычисления. Они затратили много труда на составление различных вычислительных таблиц.
Но потребность в средствах, существенно облегчающих вычислительный труд, становилась все более острой, и тогда были созданы таблицы логарифмов.
Слово "логарифм" - греческое. Оно составлено из двух слов: "logos" - отношение и "arithmos" - число. Таким образом, логарифм означает - "число, измеряющее отношение".
На чем же основаны удивительные свойства этих чисел, облегчающие вычислительный труд человека?
Несколько простых примеров помогут нам в этом разобраться.
Возьмем какое-нибудь число, например 2, и составам таблицу чисел, полученных от возведения 2 в степень целых чисел, то есть "таблицу 2n ".
| n | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 2n | 1/16 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 |
Верхняя строчка таблицы - арифметическая прогрессия с разностью, равной единице, а нижняя - геометрическая прогрессия со знаменателем два. Этой таблицей можно уже пользоваться для упрощения вычислений.
Попробуем с ее помощью умножить 16X32. В верхней строке таблицы над этими числами стоят 4 и 5. Сложим их. Получим 9. А под девяткой в нижней строке, как видите, находится число 512. Это и будет искомый результат. Действительно, 16X32=512.
Почти так же можно найти частное от деления двух чисел, например 8 на 1/16. Но теперь нужно взять разность чисел, расположенных в таблице над ними. Она равна 7, так как 3-(-4) после раскрытия скобок и сложения дадут нам 7.
В нижней строчке по этой разности найдем искомое частное - 128.
А такое сложное действие, как извлечение кубического корня из трехзначного числа, например из 512, делается с легкостью необыкновенной.
Посудите сами! Взгляд в таблицу, и мы находим показатель степени для 512. Он равен 9. Теперь разделим его на степень кубического корня - на 3. И вот под частным, равным 3, тотчас же появляется ответ - 8. Это и есть значение корня.
Наша таблица очень примитивна, но все же дает наглядное представление об общих свойствах членов арифметической и геометрической прогрессии. Они-то и могут быть использованы для упрощения вычислений. Каким образом?
...с таблицей логарифмов и без нее
Если бы мы попытались разъяснить это словами, то пришлось бы написать много скучных фраз. А вот рисунок наглядно показывает, что умножению и делению чисел геометрической прогрессии соответствует в арифметической прогрессии сложение и вычитание. А возвышение в степень и извлечение корня заменяются умножением и делением.
Расположите все восемь действий, о которых мы говорим, по степени сложности, и ваша таблица превратится в удивительные ступеньки. Сделал шаг - упрощение, сделал другой - совсем просто!
Само собой разумеется, что Составленная нами таблица пригодна только для вычислений, связанных с целыми числами, и то не с любыми. С ее помощью нельзя перемножить, например, такие числа, как 3,5 на 1,2.
Настоящие рабочие таблицы логарифмов для точных вычислений впервые построил Джон Непер. Над их составлением выдающийся шотландский математик трудился около 20 лет.
О причинах, побудивших его к этому, сам Непер говорил:
"Я старался, насколько мог и умел, отделаться от трудности и скуки вычислений, докучность которых обычно отпугивает весьма многих от изучения математики".
В предисловии к своим таблицам он писал: "Уведомление. Так как вычисление этой таблицы, которое должно было бы выполняться при участии многих вычислителей, сделано трудом одного человека, то неудивительно, если в нее вкрались многие ошибки. Произошло ли это вследствие утомления вычислителя, или по небрежности типографа, за них прошу извинения у благосклонных читателей. Однако если я увижу, что ученым приятна польза этого изобретения, то, может быть, в скором времени я дам объяснение способа, как улучшить это сочинение, чтобы трудом многих вычислителей выпустить его в свет более точно исполненным, чем было возможно для одного. Ничто сначала не бывает совершенным..."
Обещанное сочинение с объяснением способа составления таблиц появилось в свет только в 1619 году, уже после смерти автора.
В своих таблицах Непер принял за начальный член геометрической прогрессии число, равное десяти миллионам, а знаменатель прогрессии равным 0,9999999. Таким образом, он строил таблицу по убывающей прогрессии и провел огромные и сложные вычисления. Он довел прогрессию до единицы, то есть до одной десятимиллионной начального числа. Поистине титанический труд, на который не каждый отважится!
Но выдающееся значение работ Непера не только в этом. Он раскрыл сущность логарифма как новой, до него неизвестной математической зависимости.
Открытие этой зависимости имело для вычислительной математики столь же большое значение, как и открытие тригонометрических функций.

Теперь, когда мы рассказали обо всем, кроме самого главного, - что же такое логарифм, - попытаемся это сделать несколько необычным способом.
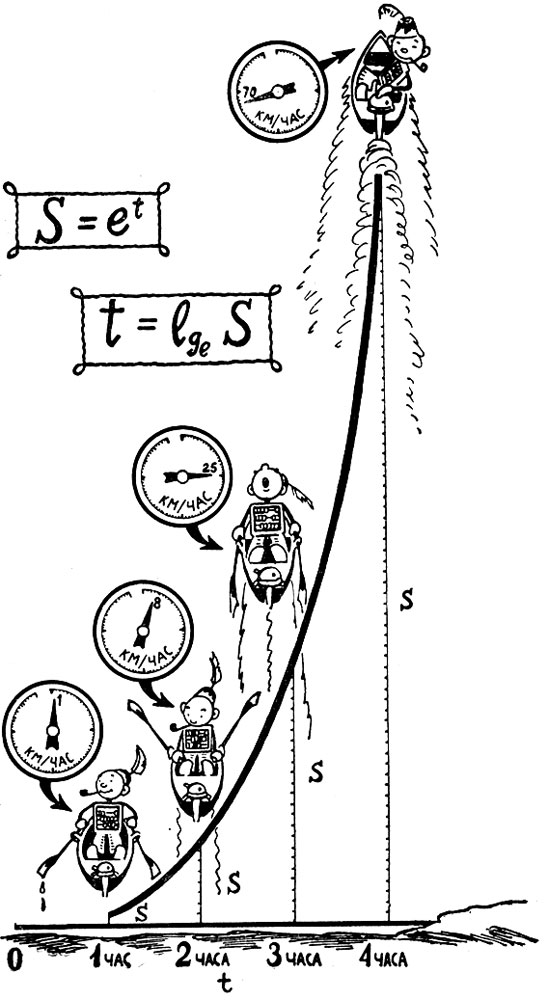
Сядем в лодку, которая находится на расстоянии одного километра от берега, и поплывем прямо от него, но с одним условием. Грести будем так, чтобы скорость лодки всегда была в точности равна ее расстоянию от берега.

Действиям над числами в геометрической прогрессии соответствуют более простые действия над ними в арифметической прогрессии
Это значит, что вначале ее скорость должна быть равна одному километру в час. Когда лодка будет на расстоянии двух километров от берега, то ее скорость надо увеличить вдвое, при расстоянии в три километра - ее скорость должна быть равной трем километрам в час и так далее.
Само собой разумеется, вряд ли кто сумеет долго выдержать такой темп движения. По этому условию, отойдя на пятьдесят километров, лодка должна мчаться по воде, подобно глиссеру - со скоростью 50 километров в час.
Но для наших теоретических рассуждений мы можем не считаться с тяжелым положением гребцов.
Движение лодки будет обладать интересным свойством. Оказывается, расстояние, на котором лодка будет через час, нельзя абсолютно точно вычислить. Как число тг, оно выражается приближенной величиной.
Гениальный математик Эйлер дал формулу, по которой это число можно вычислить с какой угодно точностью. В честь Эйлера число обозначили буквой "е" по начальной букве фамилии Euler. Оно равно 2,718281828459045... В практике е обычно принимают равным 2,72.
Итак, через час наша лодка будет находиться на расстоянии, равном е - приблизительно 2,72 километра, а ее скорость достигнет е километров в час.
Но уже через два часа расстояние станет е2 километров, а через три часа - е3 и так далее, как это показано в таблице.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| en | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 |
Вдумайтесь, что это значит, и вам станет ясным свойство этого интересного движения. Если время меняется по арифметической прогрессии, то расстояние - по геометрической.
Знаменателем геометрической прогрессии является число е. Впервые приближенное значение его нашел Непер и принял его за основание логарифмов. Поэтому они называются неперовыми, или натуральными, логарифмами.
Но для многих вычислительных работ более удобны таблицы логарифмов с основанием не 2 и не а 10. Ими пользуются и в школе.
Расстояние (s) и время (t) связано логарифмической зависимостью. Она показана кривой Непера
Таблицы десятичных логарифмов впервые составил современник Непера английский математик Генри Бригг. На него сочинения Непера произвели огромное впечатление.
"Своими новыми и удивительными логарифмами Непер заставил меня работать головой и руками, - писал ученый. - Я надеюсь увидеть его летом, так как никогда не читал книги, которая нравилась бы мне больше и приводила бы в большее изумление".
Бригг выполнил обещание и посетил в Шотландии изобретателя логарифмов. "Я предпринял это долгое путешествие, - сказал Бригг при встрече, - с единственной целью видеть вас и узнать, с помощью какого орудия остроумия и искусства были вы приведены к первой мысли о превосходном пособии для астрономов - логарифмах. Впрочем, теперь я больше удивляюсь тому, что никто не нашел их раньше, - настолько кажутся они простыми, после того как о них знаешь".
Вскоре Бригг выпустил свои четырнадцатизначные десятичные таблицы логарифмов. Спустя несколько лет их сменили десятичные таблицы голландского математика А. Влакка.

Логарифмические линейки бывают разные
Со времени гениального изобретения Непера прошло около 350 лет. Более чем 500 различных образцов таблиц логарифмов было с тех пор выпущено в свет. Они прочно вошли в арсенал вычислительных средств и до настоящего времени занимают почетное место как самое массовое пособие, облегчающее вычислительный труд человека.
Миллионы специалистов пользуются в своей повседневной работе логарифмами, начиная со сверхточных - двадцати- и более значных таблиц и кончая "деревянными логарифмами" - счетными линейками - незаменимым средством технических расчетов.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'