Один час истории

Один час истории! Много ли это?.. Далеко, далеко в океане возвышается одинокая скала. Сюда прилетают птицы. Они чистят острые клювы о твердый гранит утеса. И так из года в год. Крупица за крупицей стирается скала. Когда остатки одинокого утеса скроются под холодными водами океана, пройдет всего лишь один час истории вселенной.

Жизнь нашей планеты измеряется миллиардами лет, и по сравнению с этим временем история человечества - один час.

Первые люди на Земле появились около миллиона лет назад, но только четыре тысячи лет существуют самые древние памятники математических знаний людей.

Немногим более двух тысяч лет прошло со времени зарождения математической науки, но только триста лет назад гениальные ученые Лейбниц и Ньютон создали основы математического анализа - науки о бесконечно малых величинах. Он составляет ядро всей современной математики и многих смежных с ней наук.

Триста лет из миллиона! Всего "один час" из жизни человечества.

Медленно, ощупью познавали люди таинственные законы природы. Медленно, но неуклонно накапливали они факты. А из отдельных фактов складывались знания. Они проверялись тысячелетним опытом и вызывали к жизни новые знания.

Когда остатки скалы скроются под холодными водами океана, пройдет всего лишь один час истории вселенной

Человеческое общество двигалось вперед по пути, начертанному объективными законами. Из поколения в поколение передавался опыт, передавались знания. Ничто не могло приостановить и повернуть вспять процесс познания природы. Опустошительные войны, моровые стихии и воинствующие мракобесы замедляли его порой. Но гений человека не прекращал своего извечного движения вперед.

Много тысячелетий прошло, пока люди встали на путь точного математического анализа, научились обобщать накопленные знания и опыт, почувствовали силу этого обобщения и сделали математику мощным орудием развития общества.

И тогда-то "один час истории" стал тремястами лет непрерывного триумфального шествия математики, торжества математической науки!

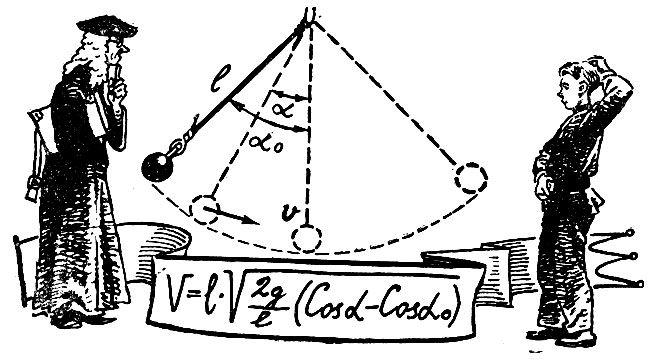
Задача, перед которой встали бы в тупик и средневековый математик и десятиклассник

Двадцати метров папируса Рейнда оказалось достаточно для записи всех математических знаний древних египтян.

Вавилонская математическая энциклопедия разместилась уже на сорока четырех глиняных плитках.

Энциклопедия математических и астрономических знаний греков заняла целых тринадцать томов "Альмагеста" Птолемея.

А труды математиков, написанные за последние триста лет, - это десятки тысяч книг и статей.

Упорная творческая работа многочисленной армии ученых не прекращается ни на один день. Гигантским прогрессом во всех отраслях науки и техники ознаменован этот период в истории человеческого общества. Этот прогресс послужил могучим стимулом для развития математики, поставил перед нею новые проблемы, новые задачи. Их решение было жизненно необходимо для подчинения сил природы разуму человека.

Математические знания, которые мы теперь получаем в школе, превосходят знания древних ученых. Многие десятиклассники могли бы одержать победы в математических турнирах с выдающимися математиками XVI столетия.

Но вот простая на первый взгляд задача поставила бы в тупик и средневекового математика и десятиклассника: найти закон, по которому меняется скорость тяжелого шарика, качающегося на нитке.

Верхушка радиомачты постоянно колеблется. Конечно, не так сильно, как показано на рисунке

Здесь силы, на которые разложена сила тяжести шарика, меняются во времени. А следовательно, меняется и его ускорение. Решение такой задачи уже не по плечу человеку, не знающему методов математического анализа, незнакомому с дифференциальными уравнениями.

Все, что нас окружает, находится в непрестанном движении: меняется с течением времени взаимное расположение планет нашей солнечной системы, температура и давление воздуха, силы, действующие в машине, токи, протекающие в электрической цепи, состояние живой клетки.

В одних случаях изменения происходят очень медленно: чтобы их заметить, не хватает жизни целого поколения. И когда изучают такие медленно изменяющиеся процессы, то даже считают их неизменными во времени. Их называют статическими.

"Вечной мерзлотой" называют определенное состояние почвы на севере. Но ученые знают, что вечная мерзлота совсем не вечна. Отрицательная температура в некоторой части земной коры держится от нескольких лет до тысячелетий. Но, несмотря на это, очень часто при исследованиях ее считают статичной, постоянной, "вечной".

Когда люди смотрят на высокую ажурную радиомачту, вряд ли они задумываются над тем, что она находится в непрерывном движении; Изменение окружающей температуры меняет ее длину. Ветер раскачивает мачту, и с течением времени меняется положение ее верхушки. Все эти перемещения происходят очень медленно, поэтому инженеры рассчитывают мачту как статическую неподвижную систему. Они пользуются при этом алгебраическими уравнениями и формулами, которые не учитывают изменений, происходящих во времени.

Но часто ученым и инженерам важно знать, как будут изменяться во времени разнообразные процессы в живой и неживой природе, особенно когда они протекают с огромными скоростями и длятся сотые, тысячные и даже миллионные доли секунды.

Стремительно падает давление воздуха в районе, к которому приближается циклон. С колоссальным ускорением движутся элементарные частицы в синхрофазотроне. Они за секунды пробегают космические расстояния. И при исследовании подобных процессов - их называют динамическими - ученых прежде всего интересует, как они изменяются во времени.

В короткие промежутки времени изменяется движение механизмов в быстроходных автоматах, растут и падают токи в электрических цепях и почти незаметно вибрируют в машинах детали.

Для создания и совершенствования таких механизмов нужно знать количественные закономерности, которым подчиняются эти динамические процессы. Иначе ничтожные вибрации станут грозной силой и разрушат самые прочные узлы. А стремительно нарастающие токи выведут из строя сложные электрические системы.

Задача о тяжелом шарике, качающемся на нитке, простейшая из таких задач. Но и перед ней алгебра оказалась бессильной.

Вибрации в работающей машине мы не всегда видим. но они всегда существуют

Для анализа и расчета динамических процессов нужны математические методы, которые, подобно сверхскоростному киноаппарату, позволяют улавливать изменения, происходящие в ничтожно малые промежутки времени. Это методы дифференциального и интегрального исчисления - науки о бесконечно малых величинах. Ее создали гениальные математики Лейбниц, Ньютон, Эйлер и их ученики и последователи.

Но одно дело исследовать явления столь же закономерные, как смена дня и ночи или чередование времен года, и совершенно другое дело изучать процессы, подверженные воздействию различных случайных обстоятельств.

Близость раскаленной печки привела к определенной закономерности в движении колеса рулетки. Этим воспользовался Смок

Монета, брошенная вверх, с неизбежностью падает на землю. Мы можем даже вычислить, через сколько секунд это произойдет. Но никакими расчетами нельзя предугадать, упадет она гербом или решкой: тот или иной исход одинаково возможен и зависит! от множества случайных обстоятельств.

Случайные явления издавна привлекали людей загадочностью законов, которые ими управляют. Немало написано романов, повестей и рассказов, где герои пытаются найти закономерности в хаосе случайностей, которыми сопровождаются азартные игры. Игроки, вероятно, хотели бы знать эти закономерности, чтобы обогатиться. Но...

Вспомните трагическую судьбу Германа из "Пиковой дамы", пытавшегося узнать счастливое сочетание карт.

Правда, бывало и так: игрок умело использовал особые условия, влияющие на случайный исход игры, и выигрывал. Такой случай описал Джек Лондон в рассказе "Малыш видит сны".

Герой рассказа Смок, играя в рулетку, знал, что у игроков всегда меньше шансов на выигрыш, чем у крупье. Но он много дней наблюдал за игрой и заметил одно обстоятельство, позволившее ему беспрерывно брать одну за другой большие ставки.

Чем больше снарядов выпущено, тем точнее наше предвидение - средняя точка попадания

Владельцы игорных столов захотели узнать секрет Смока.

- Вы нас всех озадачили, - говорили они ему. - Мы ничего не понимаем. Нам известно, что в рулетке не может быть никаких систем. Это говорят все ученые-математики. Рулетка сама по себе система, и все другие системы против нее бессильны, в противном случае арифметика - чушь.

Но Смок продолжал выигрывать. Тогда владельцам рулетки пришлось выкупить у него "секрет".

Оказалось, что никакого секрета нет. Просто игорный стол стоял близко к раскаленной печке, и колесо рулетки рассохлось, покоробилось. Это привело к появлению определенной закономерности в игре, которую и заметил хитрый Смок, изучивший повадки колеса.

Игры, основой которых является случайный исход, интересовали таких выдающихся математиков, как Паскаль и Ферма. Зародилась новая отрасль математических знаний - "теория вероятностей". Было доказано, что "вероятность" - величина, доступная измерению.

Но только в XIX веке трудами великих математиков К. Ф. Гаусса, П. Л. Чебышева, А. А. Маркова, А. М. Ляпунова теория вероятностей из собрания математических курьезов превратилась в самостоятельную науку. Из игровых задач родились отрасли математики, получившие в дальнейшем огромное практическое применение.

По словам крупнейшего советского математика А. Н. Колмогорова, выдающиеся работы Чебышева, Маркова и Ляпунова теперь всюду воспринимаются как исходный пункт всего дальнейшего развития теории вероятностей.

Вот несколько примеров,, когда человек вынужден рассчитывать на вероятность, а не на достоверность.

Известно, что пули, выпущенные из винтовки, даже неподвижно укрепленной, не попадают в одну и ту же точку мишени. Дуновение ветерка, малейшее дрожание дула, небольшое отклонение в весе порохового заряда, в весе и форме пули - все это приводит к рассеиванию точек попадания. Никакими формулами невозможно определить заранее, на каком расстоянии от центра мишени ляжет пуля. Оно будет случайным.

При самой точной настройке автоматического токарного станка размеры двух обработанных на нем деталей никогда не совпадают. Вибрации станка, износ резца, изменение его температуры и многие другие факторы приводят к отклонениям в размерах деталей. И невозможно заранее предвидеть, каков будет точный размер детали, сошедшей со станка. Он будет случайным.

Вес зерен пшеницы меняется от одного к другому, даже если они выращены в одинаковых условиях на самом небольшом участке. И нельзя предугадать веса зерна, взятого из того или иного колоса. Вес зерна будет случайным.

Но математики сделали поразительное открытие. Случайные величины, оказывается, подчиняются совсем не случайным закономерностям. Ими управляет закон больших чисел.

Что же это за удивительный закон, которому подвластны такие непокорные, сложные явления?

Хотя мы не знаем наперед, где точно ляжет пуля, сколько точно будет весить каждое зерно, как точны будут размеры деталей, но мы можем предвидеть и среднюю точку попадания всех пуль, и средний вес всех зерен, и средние размеры всей партии деталей. Более того, математика столь сильна, что может заранее предсказать, в каких пределах будут находиться различные отклонения от средней величины.

И чем больше пуль выпущено, чем больше зерен взвешено и деталей произведено, тем точнее будет наше предвидение - среднее число.

В бесконечном разнообразии явлений в физических, биологических и экономических процессах проявляется закон больших чисел. Математики раскрыли его, сняли таинственный покров со случайных явлений и вооружили ученых могучим средством анализа и управления случайными процессами.

Математики не строят машин и зданий, в их кабинетах нет весов и колб, гальванометров и микроскопов, они не производят опытов. Но математики вооружают машиностроителей и архитекторов, физиков и химиков, биологов и экономистов умением составлять и решать уравнения, вооружают целым арсеналом методов для изучения сложных процессов.

Математика опережает и наблюдения и опыт. Для математика, как и для поэта, нет границ. Он может, сидя за столом, побывать в космосе и в микромире, пробиться к центру Земли и познать тайну живого.

Математика постепенно проникла во все области деятельности человека. Она стала общим языком, на котором говорят все точные науки. Она вошла в области знаний, которые еще совсем недавно казались для нее недоступными: биологию, экономику, языкознание. Она стала "правительницей всех мыслительных изысканий" и навсегда изменила путь естествознания.