Руководство к действию

Более тысячи лет тому назад выдающийся узбекский математик Мухаммед ал-Хорезми написал учебник "Арифметика индусскими цифрами". По нему европейцы научились индийскому счету с помощью десяти цифр и узнали правила арифметических действий над ними.

"Ал-Хорезми повествует в этой книге об индусском способе счета", - так начинался латинский перевод учебника. Он произвел в те времена такое огромное впечатление на математиков, что словом "ал-хорезм", а потом похожим на него словом "алгоритм" долгое время называли арифметику в десятипозиционной системе счисления.

Это и неудивительно. Ведь многие столетия люди привыкли к мысли о том, что правила счета необычайно сложны и только небольшое число избранных может научиться этому искусству.

Но вот оказалось, что существуют такие способы счета, которые легко усваивает даже ребенок, а арифметические действия можно производить, не задумываясь над их смыслом, почти автоматически.

Первоклассник, только что перешагнувший порог школы, начинает свое знакомство с арифметикой со счета по единицам.

"Отложи на счетах столько косточек, сколько единиц в первой цифре, и прибавь к ним число косточек, равное числу единиц второй цифры. После этого сосчитай сумму" - по этим указаниям складывает первоклассник одноразрядные числа на больших школьных счетах. А если к ним добавить указания о переносе десятков, то этого уже достаточно, чтобы посредством нескольких простых операций складывать любые многозначные числа.

По мере того как маленький первоклассник подрастает и переходит из класса в класс, ен узнает правила выполнения все более сложных арифметических действий: правила извлечения корней, решения уравнений и построения геометрических фигур. Математики вместо слова "правило" обычно пользуются словом "алгоритм".

Обратите внимание на название этой главы. У многих читателей оно, вероятно, вызовет недоумение. "Технология математики"! Что это такое? Что общего между абстрактной наукой и сугубо практическим, производственным понятием "технология"?!

Происхождение слова 'алгоритм'

Но оказывается, что и математика не может обойтись без своей технологии - технологии решения математических задач. Она-то и определяет путь от уравнения или формулы к конечному результату, выраженному в конкретных числах.

Строго и точно регламентирован процесс рождения машины на заводе. Технологическая карта сопровождает каждую деталь машины. Это инструкция, свод правил, указывающих, из какого материала, на каких станках, в какой последовательности, с какой точностью должна быть изготовлена деталь и каким способом проверить ее пригодность.

Из простых деталей собирается узел, из узлов собирается машина. И здесь технологические карты указывают порядок сборки. Его строго и точно соблюдает каждый рабочий.

Так из множества простых, элементарных операций составляется технологический процесс производства самой сложной машины.

Точно так же и в математике из множества самых простых, элементарных операций складывается технологический процесс решения самой сложной задачи. Он всегда сводится к многократному выполнению в определенном порядке четырех арифметических действий.

Общий принцип расчленения сложных вычислительных процессов на самые элементарные операции имеет важнейшее значение в современной вычислительной математике.

Древнее слово "алгоритм" приобрело теперь чрезвычайно широкий смысл. Это точное указание о порядке решения сложной задачи посредством ряда простых операций. Иными словами, алгоритм - это руководство к действию для решения задач, и его можно даже облечь в форму кратких приказов, которые нужно выполнять точно и беспрекословно.

Вот пример такого руководства к действию для отыскания общего наибольшего делителя двух чисел а и b - алгоритм Эвклида. Это руководство состоит из пяти указаний:

Первое. Обозревай оба числа: а, b. Переходи к следующему указанию.

Второе. Сравни обозреваемые числа (а равно b, или а меньше b, или а больше b) и переходи к следующему указанию.

Третье. Если обозреваемые числа равны, то прекрати вычисления: каждое из чисел дает искомый результат. Если числа не равны, переходи к следующему указанию.

Четвертое. Если первое число меньше второго, переставь их местами. Переходи к следующему указанию.

Пятое. Вычитай второе число из первого. Обозревай два числа: вычитаемое и остаток. Переходи к указанию второму.

Итак, после выполнения всех пяти указаний нужно снова вернуться ко второму, затем к третьему, четвертому и пятому. Если вновь полученные вычитаемое и остаток опять не равны, снова переходи к указанию второму, и так далее, пока обозреваемые числа не станут равны. Тогда вычисление заканчивается...

Выберем сами пару любых чисел, например 21 и 14, и попробуем, следуя этим правилам, найти их общий наибольший делитель. Действуем согласно указаниям:

Первое. Обозреваем числа 21 и 14.

Второе. Сравниваем их: они не равны.

Третье. Так как числа не равны, то переходим к следующему указанию.

Четвертое. Первое число больше второго.

Пятое. Вычитаем: 21-14=7. Обозреваем вычитаемое 14 и остаток 7.

Опять возвращаемся ко второму указанию: сравниваем 14 и 7.

Сравниваемые числа не равны.

Первое число больше второго.

Из 14 вычитаем 7, получим 7. Обозреваем вычитаемое 7 и остаток 7. И опять возвращаемся ко второму указанию.

Сравниваем вычитаемое и остаток. Сравниваемые числа равны.

Вычисление прекращаем.

Таким образом, общий наибольший делитель чисел 21 и 14 равен 7.

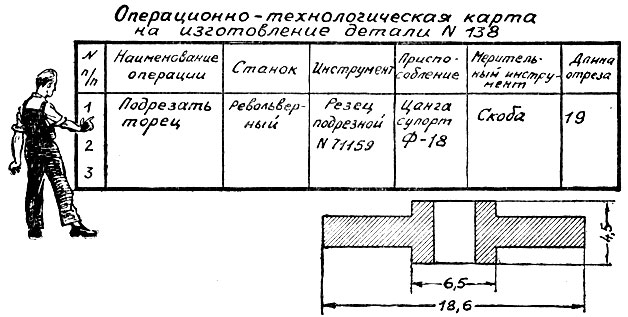
Технологическая карта сопровождает изготовление каждой детали

"Стоит ли разводить такую канитель для того, чтобы вычислить общий наибольший делитель для двух немудреных чисел 21 и 14?" - скажет нам читатель.

Далеко не всегда нужно педантично и формально составлять руководство к действию, как это сделано у нас. Но в некоторых случаях этого набора указаний будет даже недостаточно. Все зависит от квалификации человека, пользующегося руководством к действию при решении задачи.

Предположим, что вычислитель не знает, как производить вычитание. Тогда пятое указание нужно было бы развернуть в целое руководство к действию и дать правила вычитания - указать его алгоритм. Ну, а вычислителю, знающему порядок отыскания общего наибольшего делителя, достаточно дать такое указание: "Найти общий наибольший делитель для двух заданных чисел".

Но всякий алгоритм, как руководство к действию, должен удовлетворять определенным требованиям.

Во-первых, каждый, кто точно выполняет руководство к действию при решении одинаковых задач, должен получать одинаковые результаты вычислений.

Во-вторых, чтобы алгоритм был пригоден для решения не одной какой-нибудь конкретной задачи, а всех задач данного типа.

Алгоритм Эвклида не мог бы служить руководством к действию, если бы годился только для одной пары чисел, например взятых нами 21 и 14. Ведь тогда для вычисления общего наибольшего делителя для других пар чисел каждый раз приходилось бы искать новые правила. А это значит: человек никогда не научился бы решать даже такие простые задачи, как отыскание общего наибольшего делителя.

Формула, с помощью которой решается квадратное уравнение, - это тоже алгоритм. Она показывает, что нужно сделать с содержащимися в уравнении числами, вычисляя корни.

Чтобы найти и разработать алгоритм, нужно иметь обширные математические знания и затратить много творческого труда. Это может сделать только очень квалифицированный математик.

Но вот алгоритм найден, и порядок решения задачи строго определен. Каждая отдельная вычислительная операция регламентирована, и для решения задачи остается только точно и беспрекословно следовать указаниям руководства к действию. Это может выполнить уже любой человек, действуя совершенно машинально.

Человек работает машинально! Когда мы так говорим, то тут же у нас возникает мысль: а нельзя ли поручить машине выполнение этой работы? Нельзя ли машине передать на исполнение руководство к действию при решении математической задачи?

Оказывается, можно! Но чем сложнее алгоритм, тем труднее построить машину для его реализации.

Сравнительно просто создать машину, которая автоматически складывает или вычитает многозначные числа. Сложнее сконструировать машину для автоматического выполнения четырех арифметических действий. Еще труднее построить машину для решения сложных математических задач.

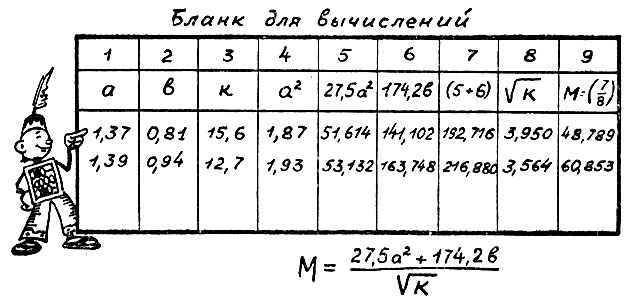
Бланк для вычислений сопровождает каждый процесс вычислений

Но ученые и инженеры умеют теперь автоматизировать решение любой математической задачи, для которой существует алгоритм и удается составить руководство к действию, выполнимое машиной.

Красной нитью через всю историю математики проходит борьба за алгоритм. Ведь каждый новый алгоритм - это решение нового типа задач, новый путь к результату. И чем проще и короче руководство к действию, тем ближе победа над тайнами математики, спрятанными за сложными формулами и уравнениями.

12 февраля 1535 года в итальянском городе Болонье царило необычайное оживление. Со всех концов Италии и даже из других стран средневековой Европы сюда съехались математики, искусные вычислители и любители всякого рода состязаний. На этот день было назначено начало математического турнира.

"Математик Фиоре вызывает на поединок каждого, кто желает состязаться с ним в искусстве решения сложных задач. Побеждает тот, кто решит больше задач из числа предложенных его противником", - так гласило объявление о правилах предстоящего турнира."

Вызов Фиоре был принят Николо Тарталья, доселе малоизвестным преподавателем математики из Брешии.

Он оказался победителем турнира, решив все 30 задач, предложенных Фиоре. Последний же не сумел решить ни одной задачи Тарталья!

Каким же образом Николо Тарталья удалось одержать столь блестящую победу, не оставлявшую никаких сомнений в его огромном превосходстве над противником, зачинщиком трудного поединка?

Ответ на вопрос дают события, предшествующие описываемому турниру.

Примерно за десять лет до этого в Болонском университете скончался профессор математики Сципион Дель Ферро. Незадолго до смерти ему удалось найти общий метод решения кубического уравнения. Об успешном результате своего многолетнего труда он сообщил только своему зятю и преемнику по должности Анабеллу делла-Нове. Но о нем неведомыми путями узнал и некий Фиоре. Получив в свои руки алгоритм решения задачи, с которой не могли справиться ни греки, ни арабы и ни ученые средневековой Европы, Фиоре бросил вызов математикам.

Обладание формулой профессора Ферро, казалось, гарантировало ему победу. Но его уверенность не оправдалась. Против него выступил действительно высокоодаренный Николо Тарталья.

Математический турнир был, конечно, не таким

Тяжелыми были детские годы Тарталья. Его родной дом, как и дома многих бедных итальянцев, был разорен французами. Мальчика ранил французский солдат, и ребенок остался на всю жизнь заикой. Имя "Тарталья" и означает "заика". У него были гениальные способности математика и огромное трудолюбие.

Приняв вызов, он сперва думал, что легко победит такого малосведущего математика, как Фиоре. Но всего за несколько дней до турнира узнал, что его противник знает алгоритм умершего Ферро. Тогда Тарталья огромным напряжением ума самостоятельно нашел еще более совершенный алгоритм. С его помощью он и одержал блестящую победу в турнире.

Алгоритм Тарталья, в последующем развитый итальянским математиком Кардано, сохранился до наших дней в виде общего метода решения кубических уравнений.

Но многие алгоритмы, открытые участниками математических турниров, так и остались секретом их изобретателей. Вот один из таких примеров.

В начале XIII века в городе Пизе жил известный математик и искусный вычислитель Леонардо. В истории его знают под именем Фибоначчи - сын Боначчи. В 1202 году он издал одну из первых в Европе книг по арифметике и алгебре, в которой излагалась десятичная система счисления.

Репутация Фибоначчи как математика и вычислителя привлекла внимание государя Римской империи Фридриха II. В сопровождении большой свиты он приехал в Пизу, где в его честь был устроен математический турнир. Одна из турнирных задач имела такое содержание:

"Найти полный квадрат, остающийся полным квадратом как после увеличения его, так и после уменьшения его на пять".

Напомним, что полным квадратом называют число, из которого точно извлекается квадратный корень.

Фибоначчи после некоторых размышлений нашел такое число. Оно оказалось равным 1681/144, или (44/12)².

Действительно:

1681/144-5+961/144+(31/12)², a 1681/144+5=2401/144=(49/12)².

Способ решения Фибоначчи так и остался неизвестным. Несомненно только, что ему удалось найти какой-то удачный алгоритм.

Теперь мы, конечно, умеем решать такие задачи. Математика располагает для того соответствующим алгоритмом.

А можно ли турнирную задачу решить самым простым путем - подобрать числа? Можно, но такой подбор сопряжен с огромной вычислительной работой.

Попробуйте решить таким способом самую простую задачу - разбить заданное число, например 68, на два, но чтобы их произведение было максимальным. Попытайтесь вначале найти эти числа подбором. Вы тотчас же убедитесь, насколько несовершенен этот способ. Между тем не трудно найти простой алгоритм, пригодный для быстрого решения задачи при любом заданном числе.

Оказывается, любое число нужно разделить пополам, и тогда произведение, образуемое этими двумя частями, будет максимальным. В нашем примере такими числами будут - 34 и 34.

У читателя после наших рассказов может создаться впечатление, что большинство способов решения математических задач обязано своим открытием поединкам между выдающимися математиками. Конечно, это не так! Только очень незначительная часть огромного арсенала алгоритмов, которым располагает современная математика, сохранилась со времен математических турниров.

Еще в древности ученые разрабатывали правила для решения различных задач. Например, одно из древнейших математических произведений - "Девять отделов арифметики", написанное в Китае за 2 600 лет до нашего летосчисления, есть не что иное, как сборник практических правил для выполнения всех арифметических действий.

В тиши кабинетов, в стенах многочисленных институтов и университетов ученые создавали и совершенствовали алгоритмы. И хотя в настоящее время известны общие методы решения почти всех существующих типов математических задач, упорная и творческая работа над алгоритмами не прекращается ни на минуту. Можно сказать, что в вычислительной математике все подчинено единой цели - отысканию алгоритмов для решения различных задач.

Особое внимание уделяют теперь созданию алгоритмов, специально приспособленных для машинного решения задач.

А есть ли такие математические задачи, для которых до сих пор не удалось построить алгоритм, или задачи, для которых алгоритма вообще не существует? Да, и те и другие задачи известны.

Некоторые думают, что стоит проанализировать таблицы выигрышей и тогда можно будет вычислить вероятность выпадения выигрышей на ту или иную облигацию.

К сожалению, это сделать невозможно. Нельзя найти правило для предсказания "счастливого" номера. Задача, как говорят, алгоритмически неразрешима.

Диофантовы уравнения, о которых мы рассказали в предыдущей главе, относятся к числу задач с пока еще не найденным алгоритмом.

Каждый раз, когда приходится решать Диофантово уравнение нового вида, математики ищут специальные приемы. Отсутствие алгоритма не позволяет составить общего руководства к действию и автоматизировать решение этих уравнений. Поэтому древние Диофантовы уравнения до сих пор привлекают внимание математиков.

В 1901 году знаменитый математик Гильберт на Международном математическом конгрессе в Париже огласил список 20 труднейших проблем. Одна из них - десятая проблема - сформулирована так:

"Построить алгоритм - найти способ, позволяющий для любого Диофантова уравнения установить, имеет оно решение в целых числах или нет".

Даже такой ответ устроил бы математиков. Ведь когда по виду уравнения можно сказать, что оно имеет решение, то стоит потрудиться, чтобы найти его тем или иным способом, хотя бы подбором чисел.

Ну, а если это неизвестно? Тогда решение можно искать очень долго, и если оно не получается, то всегда будет неясно почему. То ли его еще мало искали, то ли его вообще не существует и незачем терять время на бесплодную работу.

Вот уже более пятидесяти лет многие выдающиеся математики пытаются решить десятую проблему Гильберта, но пока безуспешно. Некоторые математики, наоборот, пытаются доказать, что невозможно построить алгоритм, о котором говорит Гильберт. Если бы это удалось сделать, то его поиски прекратились бы и математики успокоились бы. Раз проблема Гильберта неразрешима, так незачем тратить время на ее решение.

Ни того, ни другого сделать пока не удалось. Но все больше математиков начинают думать об этой проблеме как алгоритмически неразрешимой.

Знаменитый Шерлок Холмс в повести "Багровый след" логическим путем раскрыл сложное преступление.