Всемогущие И, ИЛИ, НЕ

Этот рассказ мы начнем с неприятной истории.

В одном из классов начальной школы было разбито окно. Выбить стекло мог только кто-нибудь из четырех учеников: Леня, Дима, Толя или Миша.

При опросе детей каждый из них дал по три показания:

Леня: 1) Я не виноват, 2) Я даже не подходил к окну, 3) Миша знает, кто это сделал.

Дима: 1) Стекло разбил не я, 2) С Мишей я не был знаком до поступления в школу, 3) Это сделал Толя.

Толя: 1) Я не виновен, 2) Это сделал Миша, 3) Дима говорит неправду, утверждая, что я разбил стекло.

Миша: 1) Я не виноват, 2) Стекло разбил Леня, 3) Дима может поручиться за меня, так как знает меня со дня рождения.

При дальнейших расспросах каждый из учеников признал, что из сделанных им трех заявлений два верных и одно неверное.

Можно ли логическим путем установить виновника? Можно!

Правда, цепочка логических умозаключений, которая приводит к разгадке, довольно длинная, и в ней легко запутаться. Не у каждого хватит умения и внимания сразу во всем разобраться и не потерять какое-нибудь звено рассуждений. Но, оказывается, для таких и даже более сложных логических задач существует свой алгоритм.

Кто разбил стекло?

Так же как и для математической, решение любой логической задачи имеет свою технологию. Она составляется из простейших операций, похожих на сложение и умножение. Их выполняют по указаниям руководства к действию.

С его помощью всякий может, не задумываясь, решить сложную логическую задачу. То же самое сможет сделать автоматически машина.

Но для этого логическую задачу надо представить в виде формул и уравнений.

Обычное дело - облечь в уравнения количественные закономерности, выраженные в числах. Но разве можно заковать в формулы свободные логические рассуждения, высказанные словами?

Оказывается, не так уж давно, всего около четырехсот лет назад, математики еще не умели пользоваться формулами даже для изображения математических зависимостей. Приходилось все выражать словами. Вот как записывалась в учебнике арифметики 1514 года всем известная формула тройного правила:

 Придай заднему и переднему одинаковое наименование, 
 Преврати большее наименование в меньшее" 
 Среднее умножь на заднее 
 И раздели это на переднее. 
 То, что ты получишь, 
 И будет ответом на вопрос.

Пожалуй, не каждый теперь сумеет по этой "формуле в стихах" решить самую простую задачу на тройное правило!

Только в середине XVI века французский математик Франсуа Виета положил начало современному способу изображения математических зависимостей..

А спустя триста лет английский' математик Д. Буль, отец писательницы Э. Войнич, автора романа "Овод", создал алгебру логики.

Тогда-то математики и перевели на язык формул и уравнений логические умозаключения, выраженные словами.

Каким же образом можно изобразить в виде формулы, например, такое обычное высказывание:

"Я обязательно поеду на футбольный матч, если достану билет, или меня пригласит приятель, и если не будет дождя, и только при этих условиях"?

Всемогущие И, ИЛИ, НЕ

Для объяснения нам придется привести некоторые логические рассуждения.

В заявлении, сделанном любителем футбола (такое заявление мог бы сделать, по нашему мнению, только любитель - болельщик, конечно, не посчитался бы с погодой!), его поездка на матч оговорена рядом условий. Они выражены им в виде отдельных высказываний. Вот они:

1) я достану билет,

2) меня пригласит приятель,

3) будет дождь.

Простые высказывания могут быть связаны между собой словами ИЛИ, И, НЕ. Они появились здесь не случайно. Всегда сложные высказывания выражаются через простые с помощью этих трех слов.

А это значит, что раз и навсегда можно условиться каждое из них обозначать для краткости каким-нибудь символом, как в математике вместо слов "плюс", "минус", "умножить", "разделить" пользуются соответствующими символами.

Обычно принято слово ИЛИ обозначать крестиком "плюс" "+", а слово И - знаком умножения - точкой "o".

Теперь остается каждое простое высказывание обозначить для сокращения какой-либо буквой. А его отрицание, то есть слово НЕ, обозначать той же буквой, но с черточкой наверху. Например:

Я достану билет - Б; Я не достану билета - Б.

Меня пригласит приятель - П; меня не пригласит приятель - П.

Будет дождь - Д; не будет дождя - Д.

Запишем с помощью этих символов сложное высказывание:

"Я достану билет и не будет дождя или меня пригласит приятель и не будет дождя".

Вот эта формула:

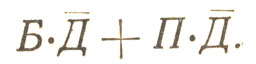
Как и в алгебре, общий множитель можно вынести за скобу и написать формулу в таком виде:

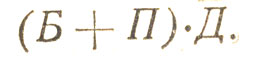
Читается она так:

"Я достану билет или меня пригласит приятель и не будет дождя".

В заявлении нашего любителя это сложное высказывание равносильно условию поездки на матч, которую мы обозначим буквой М. Теперь заявление можно написать очень кратко такой формулой:

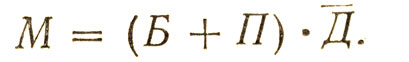
В первой главе мы рассказали о том, что всякое логическое суждение может быть либо истинным, либо ложным.

Учитель, в классе которого было разбито стекло, путем опроса установил, что из трех заявлений каждого из учеников два верных, а одно неверное. Чтобы найти виновника, надо установить, какое именно высказывание каждого ученика истинно, а какое ложно,

В математической логике условились истинное высказывание обозначать единицей - 1, а ложное нулем - 0.

"Я выучила все уроки", - заявила ученица своему классному руководителю. Обозначим это заявление для краткости буквой У. И если высказывание ученицы истинно, то У=1.

Я обязательно поеду на футбольный матч, если достану билет, или меня пригласит приятель, и если не будет дождя

Ученика, действительно выучившего уроки, такая более чем скромная оценка знаний вряд ли удовлетворит. Но с точки зрения математической логики правдивое заявление ученика получило наивысшую оценку. (Кстати, в Чехословакии и Венгрии единица действительно является наивысшей оценкой в школе.)

Теперь заметим: если У=1, то У=0, ибо в этом случае высказывание "я не выучил уроков" было бы ложным. И наоборот: если бы ученик не выучил уроки, то У=0, и тогда У=1.

Это правило является в логике общим. Если какое-либо высказывание В=1, то В=0 и, наоборот, если В=0, то В=1.

'Я выучила уроки' - истинно. 'Я выучила уроки' - ложно

Нам остается еще познакомиться с несколькими положениями математической логики, и тогда мы без труда сумеем разобраться в истории с разбитым стеклом.

Ясно, что В+В=В и В•В=В.

Действительно, сложное высказывание "я иду гулять или я иду гулять" ничем не отличается от простого высказывания "я иду гулять". Точно так же "приемник будет работать и приемник будет работать" равносильно простому высказыванию "приемник будет работать".

Столь же очевидны и следующие два положения:

В+В=1 и В•В=0.

В самом деле, сложное высказывание "дождь будет или дождя не будет" истинно в том или другом случае: оно всегда истинно. Такого рода прогноз погоды всегда был бы правильным, хотя вряд ли он кого-либо устроил бы.

А сложное высказывание "телевизор включен и телевизор не включен" всегда ложно. Соединение с помощью союза И двух противоречивых высказываний никогда не может быть истинным.

Теперь, когда мы логику претворили в формулы, зададим себе такой вопрос: можно ли "вычислить" истину? Можно ли путем вычисления найти проказника, разбившего стекло?

Вспомним, что из трех показаний каждого ученика одно ложно, а два истинных. Значит, сложное высказывание каждого из них будет истинным (равным единице), когда верно первое и второе и неверно третье показание, или верно первое и третье и неверно второе, или неверно первое и верно второе и третье.

Будем обозначать показание каждого из учеников заглавной буквой его имени с номером показания внизу. Тогда заявление Лени логично записать такой формулой:

Л=Л₁•Л₂•Л₃+Л₁•Л₂•Л₃+Л₁•Л₂•Л₃.

Точно так же изобразим показания остальных учеников.

Димы: Д=Д₁•Д₂•Д₃+Д₁•Д₂•Д₃+Д₁•Д₂•Д₃

Толи: Т=Т₁•Т₂•T₃+Т₁•T₂•T₃+Т₁•Т₂•Т₃.

Миши: М=М₁•М₂•М₃+M₁•М₂•М₃+М₁•М₂•М₃.

Если внимательно проследить показания учеников, то легко заметить, что первое и третье показания Толи равносильны. Действительно, ведь утверждение "я не виновен", по существу, не отличается от утверждения "Дима говорит неправду, что я разбил стекло". Но тогда Т₃=Т₁, а Т₃=Т₁ и его заявление можно теперь написать так: Т=Т₁•Т₂•Т₁+T₁•T₂•Т₁+T₁•T₂•T₁ или Т=(T₁•Т₁)T₂+(T₁•T₁)T₂+(T₁•T₁)T₂.

Но мы знаем уже, что противоречивые высказывания дают ложь. Поэтому (Т₁•Т₁) = 0. А если один из сомножителей равен нулю, то все произведение равно нулю и заявление Толи примет такой вид:

Т=T₁•T₁•T₂=T₁T₂.

Оно будет истинным - равным единице, если каждый из сомножителей равен единице. Следовательно: T₁=1 и Т₂=1 или Т₂=0.

Таким образом мы нашли, что первое показание Толи верно, а второе ложно. А так как он сказал: 1) Я не виновен, 2) Это сделал Миша, 3) Дима говорит неправду, утверждая, что я разбил стекло,- то ясно, что стекло разбили не Толя и не Миша.

'Вычисляют' проказника

Но теперь уже очевидно, что третье показание Димы, в котором он обвиняет Толю, ложно. Значит, Д₃=0 и Д₃=1. А раз так, то в заявлении Димы, записанном в виде формулы, последние два слагаемых обратятся в нуль и формула примет простой вид:

Д=Д₁•Д₂•Д₃.

И снова заявление будет истинным, если каждый из сомножителей равен единице. Но мы уже нашли, что Д₃=1 и, следовательно, Д₁=1 и Д₂=1.

Нашли

Первое и третье показания Димы верны. Следовательно, Дима не виновен,

Третье показание Миши противоположно второму по-казанию Димы: М₃=Д₂. Значит, М₃=0, а М₃=1 и заявление Миши теперь пишется так:

М=M₁•M₂•M₃ Оно истинно только в том случае, когда

М₁=1; М₂=1; М₃=1.

Второе показание Миши истинно! Стекло разбил Леня! Так формулы математической логики быстро и безошибочно помогли найти виновника.

Конечно, математическая логика создана не для того, чтобы искать проказников или раскрывать преступления. Работники уголовного розыска не прибегают к математическим формулам и символам. Но это не мешает им пользоваться железными законами логики для того, чтобы, сопоставляя факты, отбрасывать ложные и противоречивые показания и находить истину при самой запутанной ситуации.

Математическая логика находит широкое применение в самых различных областях науки и техники. Ее методами пользуются при создании сложных автоматических систем и, в частности, при конструировании современных вычислительных машин. Она служит основой для развития машинной математики.

Математическая логика облекла в формулы понятия, суждения и умозаключения формальной логики. Силлогизмы, о которых мы рассказывали в первой главе, воплощены в точные формулы. Строгие математические законы указывают алгоритм построения самых сложных логических умозаключений.

Но было время, когда люди думали, что можно с помощью простого комбинирования общих понятий находить всевозможные истины и даже строили для этой цели "мыслительные" машины. Такие философы мечтали с их помощью разрешить все проблемы науки, все загадки жизни, все тайны земли и неба.

"Мыслительная" машина средневекового философа, богослова и алхимика Раймунда Луллия была устроена очень просто. На большом неподвижном круге по окружности были написаны девять вопросов: "Сколько? Который из двух? Когда? Где? Какого качества?" и другие.

Внутри круга друг над другом были расположены еще пять кругов уменьшающегося диаметра. Они могли вращаться независимо друг от друга. Каждый круг делился на девять секторов - "камер", В них были сделаны надписи. В одном круге названия девяти главных грехов и добродетелей, в другом - девяти главных физических свойств.

Луллия вместил в камеры всю известную ему премудрость. Вращая те или иные круги, он передвигал их на одно, два, три деления. При этом неподвижным оставался то первый, то второй, то первый и третий или пятый и второй.

И всякий раз против вопросов главного неподвижного круга оказывались различные сочетания слов.

Ясно, что подобная машина не могла решать никаких логических задач. Ее "откровения" больше всего походили на бессмыслицу. Иначе и быть не могло. Изобретатель Раймунд Луллия хотя и называл свое детище "великим искусством", но он не имел алгоритма, не знал правил для выбора из всевозможных комбинаций суждений истинного суждения и не мог построить для своей машины руководства к действию. Несмотря на это, целое столетие люди увлекались "вертушкой понятий". Но потом ее забыли.

Однако заманчивая идея построить "мыслительный прибор" находила впоследствии сторонников и даже среди великих ученых. В XVI веке "искусством" испанского философа интересовался Джордано Бруно. В следующем веке занимался "мыслительной рулеткой" Афанасий Кирхнер. Думал над этой проблемой и знаменитый философ Лейбниц.

В вертушку Луллия вместил всю известную ему премудрость

Как видите, идея механизации логических умозаключений на протяжении многих веков не давала покоя людям науки.

Сколько людей смеялось над чудаком Гаррисом, попавшим в Хемптонкортский лабиринт!

И только в наше время, используя законы математической логики, ученые и инженеры сумели построить "мыслительные машины". Человек снабдил их руководством к действию, и они безошибочно решают сложнейшие логические задачи. Но надо твердо помнить, что "деятельность" этих машин основана на законах формальной логики. Поэтому и современная "мыслительная" машина никогда не сравнится с человеком, с существом, владеющим оружием диалектической логики.