Головокружительная арифметика

Прежде чем рассказать о головокружительной арифметике, мы вынуждены будем провести небольшое занятие.

Оно покажется совсем легким. Речь пойдет о сложении и умножении единиц.

- Позвольте! - может быть, воскликнете вы. - Такую премудрость каждый из нас изучал еще в те годы, когда с гордостью говорят: "мне скоро будет восемь!"

И тем не менее нам придется вернуться к началам арифметики. Но не обычной, а машинной.

Мы уверены, что скоро наступит такое время, когда "машинная математика" войдет в школьные программы, а пока этого нет, нам придется восполнить небольшой пробел в знаниях некоторых читателей.

Арифметические действия над числами в двоичной системе, по которой обычно работает машина, проводятся так же, как и в десятичной системе. Только в двоичной системе сложение двух единиц дает ноль в данном разряде и перенос единицы в следующий, то есть 10.

Вот как выглядит небольшая таблица сложения:

0+0=0

0+1=1

1+0=1

1+1=0 и перенос единицы в следующий разряд.

Попробуем сложить числа, которые нам встречались в главе "Язык" машины". Это 1 000, 10 и 7.

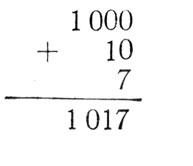
То же проделаем и с числами, записанными в двоичном счислении.

Эту запись можно проверить по способу, предложенному на странице 147. Получим 1 017.

И умножение в двоичной системе проще, чем в десятичной. Вся таблица умножения ограничивается умножением на ноль и единицу. Вот она:

0X0=0

0X1=0

1X0=0

1X1=1

Умножим 10X5=50 или 1010Х101. Умножение проводим обычным способом:

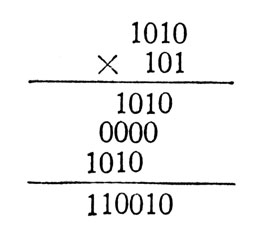
Стремяеь максимально упростить работу машины, конструкторы свели все многообразие математических операций к одному простому арифметическому действию - сложению.

Умножение выполняется последовательным сложением со сдвигом ряда чисел.

Вычитание - то же сложение, но с дополнительным числом, то есть числом, дополняющим данное до первого числа следующего высшего разряда.

Например, дополнительным числом к 3790 будет 6210 (3790+6210=10000), и чтобы вычесть 3790 из 4681, достаточно сложить 4681 с 6210. Отбросив перенос в высший разряд, получим правильный ответ - 891.

Деление сводится к последовательному вычитанию, а оно, как мы показали, в свою очередь, заменяется сложением.

Конечно, путь вычислений при этом необычайно удлиняется. Но электронные вычислительные машины не "побоялись" вернуться к "первобытной" арифметике - простому сложению. При молниеносном счете и сложении длинный путь вычислений не помеха.

Но и складывать можно по-разному: или общепринятым способом - от разряда к разряду, начиная с низших, как на бумаге, или одновременно по всем разрядам, с последующим учетом переносов, как в арифмометре. Первый способ называется последовательным, а второй параллельным.

Теперь мы можем познакомиться с работой арифметического устройства. Это, собственно, и есть тот узел машины, в котором происходит головокружительный счет.

Подобно зерну, засыпанному под мельничные жернова, сюда поступают груды необработанных чисел. Арифметическое устройство их "перемалывает" и выдает готовый результат.

Основу арифметического устройства составляет так называемый сумматор. Это естественно: ведь выполнение всех арифметических действий в конечном счете сводится к сложению и сдвигу чисел.

При первом взгляде на этот узел машины кажется: как много деталей, как они сложны! Но стоит немного присмотреться, и видишь: все сложные устройства состоят из набора однотипных ячеек - "клеток".

Хитроумные комбинации этих ячеек дают возможность строить удивительно работающие узлы, способные считать и даже логически рассуждать.

Говорят, в капле воды полностью отражается гигантское солнце. Вот так же и в маленьком быстродействующем электронном блоке-схеме отражены главный принцип устройства и основа работы большой вычислительной машины.

О том, как работает маленький считающий элемент машины - триггер, мы знаем. Посмотрим теперь, как же удалось построить приборы-схемы, способные логически "рассуждать" и подчиняться всевозможным командам.

Для этого придется вспомнить всемогущих И, ИЛИ, НЕ из главы, в которой мы, применив логику, выраженную в формулах, разыскали проказника, разбившего стекло.

Люди сумели в машине с помощью электронов записывать и считать числа. Сумели и формулы математической логики, изображаемые символами на бумаге, воплотить в электрические схемы.

Представьте себе электрическую схему, например цепь из источника тока, звонка и двух последовательных выключателей.

В такой цепи, чтобы звонок зазвонил, то есть чтобы прошел сигнал, надо включить И первый, И второй выключатели.

Подобная цепь называется схемой совпадения, или логической схемой И. В ней только при совпадении во времени обоих сигналов на выходе появляется импульс.

В другой схеме выключатели соединим параллельно. Теперь надо включить ИЛИ первый, ИЛИ второй выключатели, и тогда звонок зазвонит. Такая цепь называется схемой разделения.

Она осуществляет логическую операцию ИЛИ. Схема позволяет в одну точку подать напряжение от различных линий без замыкания их между собой.

Схему отрицания, или логическую схему НЕ, можно назвать цепью наоборот. В ней один вход и один выход. Но импульс тока на последнем появляется лишь тогда, когда на входе нет сигнала.

НЕ, И, ИЛИ в электронных схемах

Конечно, бессмысленно ставить в электронных быстродействующих машинах электрические цепи с выключателями. Здесь работают электронные лампы. Они воспроизводят те же логические операции, но с колоссальной скоростью.

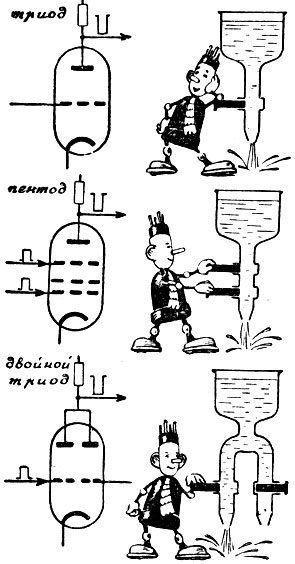
Вот три электронно-ламповые схемы. Первая - НЕ, вторая - Я, третья - ИЛИ. Как они работают?

Воспользуемся аналогией между электрическим током и водотоком. Посмотрите, как падает уровень воды в сосудах, и вам все станет ясно.

Если НЕ сдвигать задвижку, уровень воды в сосуде упадет.

Если сдвинуть И первую, И вторую задвижки, уровень воды в сосуде упадет.

Если сдвинуть ИЛИ первую, ИЛИ вторую задвижки, уровень воды в сосуде упадет.

В электронных схемах происходит примерно то же самое, только течет не вода, а электрический ток; вместо уровней жидкости - величины напряжений на выходе. Схемами управляют не задвижки, а импульсы тока.

Вот мы и получили, так сказать, овеществленные, материализованные в проводах и лампах схемы, реализующие три основные логические операции: наши всемогущие Я, ИЛИ, НЕ.

Они-то и позволяют машине "рассуждать" во время работы: Я - соединять, ИЛИ - выбирать, а НЕ - отрицать.

Если вспомните, что триггер, показывая единицу или ноль, тем самым будто говорит "да" или "нет", то станет ясно, что "язык" машины, несмотря на свою бедность, позволяет кодировать все числа, слова, вести логические рассуждения.

Читатель уже знаком с основными понятиями математической логики. Разработанные в ней методы широко используются при конструировании самых "запутанных" логических схем, построенных на реле, электронных лампах, ферритах. Важно отметить, что все они базируются на общих принципах построения и работы. Поэтому-то из них можно составлять более сложные логические схемы, которые нужны для управления и преобразования в вычислительных устройствах.

На следующей странице дан один из примеров более сложной схемы, реализующей "формулу матча". Как видите, она составлена из логических элементов: ИЛИ, НЕ, Я. Взглянув на рисунок, сами сможете проследить, как она работает.

Схема Я дает сигнал на выходе, когда получит их на обоих входах одновременно. А схема ИЛИ будет его выдавать каждый раз, когда сигнал поступит или от одного, или от другого входа.

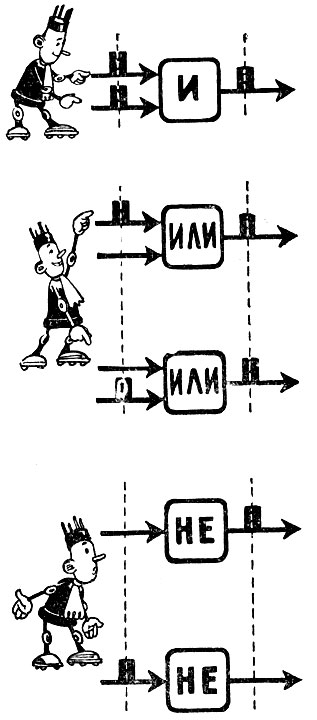
С помощью электрических импульсов выполняют логические операции

Такие схемы работают с головокружительной, не укладывающейся в обычные понятия, скоростью. Нужную логическую операцию они выполняют в микросекунды. В этом заключается еще один секрет быстродействия электронных машин.

Читатель, вероятно, уже догадывается, что мы подошли к самому главному - к рассказу о том, как же производит машина арифметические операции.

Процесс этот чрезвычайно сложен, и понять работу машины во всех ее деталях можно только после основательной предварительной подготовки читателя.

Перед раскрытием сути дела необходимо хотя бы очень кратко ознакомиться и с математической, и с логической, и с технической, и даже с историческои сторонами дела. Без этого очень трудно понять, как же люди дошли до создания потрясающего по своей силе изобретения - быстродействующих вычислительных машин.

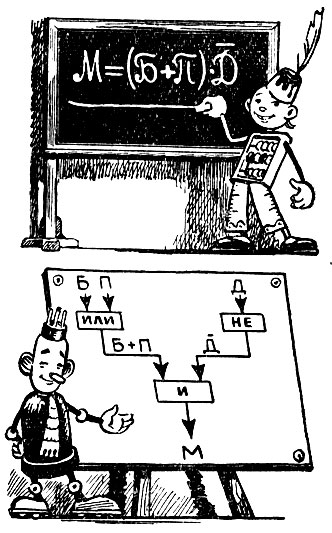
Логическая схема 'формулы матча'

Вот почему, прежде чем рассказывать о работе основного узла машины, мы так много места уделили разделам книги, подготавливающим читателя к главному. И если читатель уяснит себе работу "электронного вычислителя", ему легко будет понять и последующие рассказы о кибернетической технике и ее возможностях.

Сумматоры - вот, собственно, кто выполняет в машине основной вычислительный труд.

Существует много типов сумматоров, но все они подразделяются на две группы: последовательного и параллельного действия. Это зависит от способа сложения, который принят конструктором.

Последовательный сумматор более прост, но работает медленнее. Параллельный, наоборот, работает быстрее, но более сложен.

Высокая скорость работы, как правило, требует более сложной конструкции машины.

Одношпиндельный сверлильный станок прост по устройству, но много времени надо, чтобы на нем просверлить одно за другим десятки отверстий. Многошпиндельный может сразу высверлить все отверстия. Но он сложнее.

Работа последовательного сумматора напоминает действие "движка" застежки-"молнии". Подобно раздельным сторонам застежки, в сумматор с одного конца входят вереницы чисел - слагаемые - и с другого выходят, крепко скрепленными в сумму.

По двум каналам один за другим спешат в сумматор импульсы. Это двоичные числа, составленные из нолей и единиц. Есть единица в разряде - импульс. Ноль в разряде - нет импульса.

Если бы можно было остановить стремительный бег чисел, то каждое из них предстало бы перед нами железнодорожным составом из вагонов и платформ. Вагон - импульс, платформа - импульса нет.

Сумматор складывает двоичные числа по таблице сложения, с которой мы уже знакомы.

По входным каналам поступили одновременно, единица и ноль - на выходе тотчас же появится единица; это сумма: 1+0=1. Поступили две единицы - на выходе ноль; это тоже сумма 1+1=0, но появилась единица переноса. Ее нужно сложить с цифрами следующего разряда, да так, чтобы поспеть к их приходу в сумматор. Для этого в схеме сумматора предусмотрен второй выходной канал специально для переноса. Он соединяется с входом в сумматор через линию задержки, которая может задерживать стремительный бег импульса на точно заданное время.

Работа последовательного сумматора напоминает застежку-'молнию'

Когда надо, единица переноса поступает со второго канала на вход сумматора и присоединяется к следующему разряду.

Схема сумматора - логическая схема. В ней работают воплощенные в электронные лампы Я, ИЛИ, НЕ. Они моделируют сложное высказывание.

"Импульс суммы появится, если подать импульс ИЛИ на первый, ИЛИ на второй вход сумматора, но НЕ на оба одновременно".

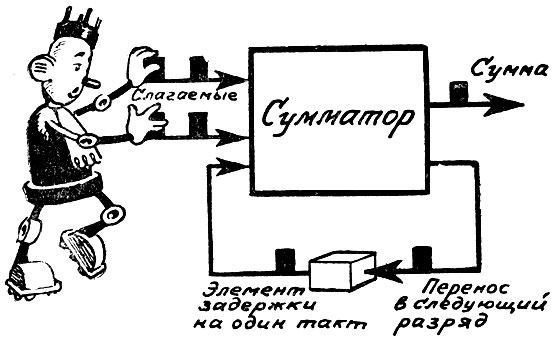
Принцип работы последовательного сумматора

"Импульс переноса появится, если поданы импульсы одновременно И на первый, И на второй входы сумматора".

Выработанные сумматором импульсы суммы поступают на цепочку из триггеров и там сосчитываются и хранятся. Это регистр суммы.

Безмолвно, в абсолютной тишине, разряд за разрядом ведет сложение сумматор. Такт его работы длится всего несколько микросекунд. Трудно представить такую скорость сложения. Мигание века глаза 7ю секунды, а здесь миллионные доли ее.

И все же это недостаточно быстро. Чтобы сложить два десятизначных числа, в последовательном сумматоре нужны десятки тактов. Последним высшим разрядам приходится "долго" ждать.

А в сумматоре параллельного действия разряды равноправны, никто никого не ждет: все цифры слагаемых поступают на сложение одновременно. Молниеносный счет ускоряется в десятки раз.

Вот его схема. Здесь знакомые нам элементы. Две цепочки триггеров выстроились друг против друга. В них слагаемые. Сколько разрядов слагаемых, столько нужно и триггеров.

Цепочки соединены магистралями. По ним побегут импульсы. На пути логические схемы - вентили. Это краны; они то открывают, то закрывают магистрали.

Все вентили одним входом подключены "а линию управления.

Дан сигнал "сложить", и на один из входов каждого вентиля поступил импульс. Но так как это логическая схема, то она выдает сигнал - единицу, если есть сигналы на обоих входах: И управляющем, И магистральном.

Поэтому в верхнюю цепочку из нижней пройдут только единицы. Здесь они сложатся с числом, уже стоящим в триггерах.

Верхняя цепочка - суммирующая. Между ее триггерами специальные схемы передают из низшего разряда в высший единицы-переносы.

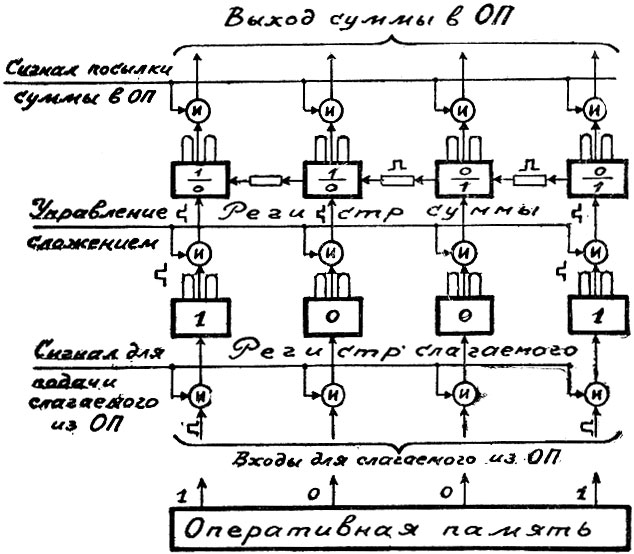
Принцип работы параллельного сумматора

В десятиразрядном сумматоре тридцать три триггера. В каждом триггере две лампы. На каждую из этих основных ламп приходится еще несколько вспомогательных. Так наша простая схема получила реальное воплощение в двухстах, трехстах электронных лампах.

А в арифметическом устройстве их еще больше. В нем, кроме сумматора, есть еще схемы умножения, вычитания, деления. Работая с сумматором, они и выполняют все арифметические действия посредством сложения.

От конструкции арифметического устройства, от того, какие в нем элементы, от того, какие операции оно может выполнять, зависят основные показатели машины: ее возможности, скорость, габариты.

Схемы параллельного действия применяют там, где хотят получить наибольшую скорость вычислений, не считаясь с затратами на оборудование.

Последовательные системы позволяют обойтись минимальным количеством аппаратуры. Поэтому их применяют в специализированных машинах. Здесь зачастую не требуются громадные скорости. Зато имеет значение размер и стоимость машины.

В новейших вычислительных машинах арифметические устройства создают на полупроводниковых элементах без применения электронных ламп. Получаются простые, надежные, компактные системы, работающие с большой скоростью и потребляющие мощность, которая исчисляется всего несколькими десятками ватт.