Электронный путеводитель
Сложный вычислительный агрегат - быстродействующая электронная машина - управляется автоматически. Работой всех ее частей очень умело руководит "УУ". Этими двумя буквами обозначается управляющее устройство машины.
Если для всех частей вычислительной машины попытаться искать сравнения, то управляющее устройство можно уподобить дирижеру большого оркестра.
Вот человек в черном фраке поднялся на помост. Взмах тонкой хрупкой палочки - ив зал полились звуки чудесной музыки.
Дирижер управляет оркестром. Он то протягивает к музыкантам руки, то воздевает их вверх, то резко опускает, то, как стрелой, пронзает магической палочкой пространство, безмолвно указывая, кому вступать в игру, кому остановиться.
И оркестранты понимают своего руководителя. Они подчиняются единой воле и действуют согласованно, слаженно.
Работу всех частей машины умело направляет 'УУ'
Управляющее устройство тоже согласовывает работу разных частей машины, подает команды: кому и когда вступать в действие, что и как делать.
Но как дирижеру необходима партитура, читая которую он ведет за собой оркестр, так и управляющему устройству нужна заранее составленная программа - своеобразный свод приказов на производство вычислений. "Читая" ее, управляющее устройство подает команды частям машины, ведет их работу по единому пути.
Программа, составленная из отдельных команд, хранится в оперативной "памяти". Это руководство к действию, по которому машина решает задачу.
Вспомните алгоритм Эвклида из главы "Руководство к действию". Пять лаконичных указаний - программа вычисления общего наибольшего делителя. Ею может пользоваться любой вычислитель, действуя совершенно машинально. Для решения задачи он должен только уметь читать и точно выполнять указания.
Аналогичную программу можно составить и для электронной вычислительной машины. Управляющее устройство должно "читать" приказы и привлекать к их выполнению остальные устройства.
Приказ на языке машины еще лаконичней, чем любое из наших пяти указаний, которые написаны Для вычислителя. Это и понятно. Ведь язык машины - язык нолей и единиц. Но каждая единица и даже каждый ноль - это триггер, это один разряд в ячейке "памяти", это лампы, ферриты, сопротивления, конденсаторы.
Поэтому все лишнее - не только слова, но даже и буквы - выбрасывается из машинного указания.
Вот как выглядит команда на языке машины: 0001•0000001010. Для непосвященного человека она совершенно непонятна. Но управляющее устройство расшифрует этот набор нолей и единиц в длинное и четкое указание - "сложить число из ячейки № 10 оперативной "памяти" с числом, стоящим в сумматоре".
Посмотрите внимательно на четырнадцатиразрядное двоичное число. Мы его разделили точкой на две части.
Первая, четырехразрядная, группа двоичных знаков - это код операции. Он указывает, что именно нужно сделать. В нашем случае код 0001 означает "сложить с числом, стоящим в сумматоре".
Вторая, десятиразрядная, группа двоичных знаков, указывает адрес ячейки "памяти". В ней находится то число, над которым нужно выполнить предписанную операцию.
В нашем примере десятиразрядная группа 0000001010 в переводе на обычную десятичную систему счисления соответствует числу 10. А всего посредством такой группы можно записать 210 или 1024 адреса. Этого достаточно для указания адреса любой из 1024 ячеек внутренней "памяти", о которой мы уже рассказывали.
Теперь стала понятной та команда, которую мы написали предельно короткой фразой -четырнадцатью двоичными знаками.
Вернемся к алгоритму Эвклида. Просмотрев все пять указаний, вы сразу заметите, что часть из них носит совершенно категорический характер. Например, указание "сравни обозреваемые числа".
Оно звучит как обычный приказ "подойди к доске" или "прочти эту книгу" и требует безоговорочного выполнения.
Указания такого типа должна выполнять при любых обстоятельствах и машина. Они поэтому называются "безусловными командами".
Иной характер носит такое указание: "если обозреваемые числа равны -прекрати вычисления, если нет - переходи к следующему указанию".
Когда мы говорим: "Реши задачу № 174. Если решишь - иди гулять; если нет - я скажу, что делать дальше", - то последующие действия человека, получившего такое указание, связаны с результатом выполнения предыдущего указания: "реши задачу № 174".
Указание, как видите, носит условный характер. Его выполнение ставится в зависимость от некоторых условий.
В алгоритме Эвклида его выполнение обусловливается равенством или неравенством сравниваемых чисел.
Электронная вычислительная машина может выполнять и условные указания. Они называются "условными командами". Получив условную команду, управляющее устройство в зависимости от результата предыдущей операции выбирает тот или иной путь для дальнейшей работы машины.
Вот пример. В ячейке № 3 оперативной "памяти" хранится команда: "если число в сумматоре стало отрицательным - переходи к выполнению команды, хранящейся в ячейке № 11. Если же оно положительно - выполняй команду из ячейки № 4".
И когда такая условная команда попадет в управляющее устройство, то оно прежде всего проверит знак числа в сумматоре. И в зависимости от результата проверки обратится за дальнейшими указаниями либо к ячейке № 11, либо к ячейке № 4.
Как же записать такое длинное указание? Сколько нужно для этого нолей и единиц? Оказывается, условную команду можно представить в таком же лаконичном виде, как и безусловную.
Условная операция кодируется той же четырехразрядной группой. В нашем коде ее можно, например, обозначить так: 0111. А остальные десять разрядов указывают номер ячейки, откуда нужно взять следующую команду.
И условная команда, хранящаяся в ячейке № 3, приобретает обычную предельную короткую запись: 0111.0000001011. Она означает: "если в сумматоре образовалось отрицательное число, то переходи к команде в ячейке № 11". А указывать вторую часть команды не нужно. Управляющее устройство знает: при других обстоятельствах следующее указание нужно искать в ячейке со следующим порядковым номером. Поэтому при положительном числе в сумматоре оно обратится за командой к ячейке №4.
В жизни часто приходится встречаться с обстоятельствами, которые заставляют прибегать к логической связи "если.." то...". Вместе со всемогущими И, ИЛИ, НЕ она сокращает и облегчает порой длинный и сложный путь логических рассуждений. Она позволяет человеку наиболее гибко координировать свое поведение в зависимости от обстоятельств.
Представьте себе, что у человека под рукою полный свод правил, в которых собраны условные указания на все случаи жизни. Ему тогда достаточно лишь произвести выбор из многих "если... то..." и взять подходящее к той или иной ситуации.
Само собой разумеется, такой список составить невозможно. Однако люди стремятся накопить "условные указания", которые мы называем опытом и квалификацией каждого человека.
А вот для вычислительной машины математики и инженеры составили список разных "если... то...", необходимых для ее работы, и воплотили их в условные команды. Они-то и придают машине замечательное свойство выбирать последующее действие в зависимости от результата предыдущего. Тем самым ее "поведение" ставится в зависимость от ситуации.
Теперь ясно, почему программа должна включать условные команды. Благодаря им она становится настоящим руководством к действию.
Попробуем составить для машины программу вычисления общего наибольшего делителя двух чисел, айв, по известному нам алгоритму Эвклида.
Для этого нужно иметь перечень операций, которые может выполнять машина. Мы не будем выписывать его полностью, а предположим, что операции, необходимые для нашей задачи, в машине предусмотрены. Сведем их в таблицу, но кодировать будем не двоичными числами, а буквами. Так удобнее составлять программу. Устройства машины сами переведут буквенные команды на понятный для нее язык. Поэтому программисты-математики составляют программы на обычном языке.
Вот небольшая таблица операций, с помощью которых мы затем составим программу.
| Название операции | Краткое обозначение |
|---|---|
| Вычесть число в ячейке №... из числа в сумматоре | Вч |
| Сравнить число в ячейке №... с числом в сумматоре | Ср |
| Переслать число из ячейки №... в сумматор, поставив сумматор предварительно на ноль | Пс |
| Переслать число из сумматора в ячейку № | Пч |
| Перейти к команде в ячейке № | Пк |
| Условная команда: если сравниваемые числа неравны, то перейти к команде в ячейке № | Ус |
| Условная команда: если число в сумматоре отрицательное, то перейти к команде в ячейке № | Ул |
| Остановить машину | Ст |
Как видите, всего восемь операций.
Еще одно небольшое предварительное замечание, и можно начать программирование. Нам придется при неравенстве чисел а и в устанавливать, какое из них больше, а какое меньше.
Человек это может сделать просто - взглянув на числа. Правда, если они многоразрядные, ему придется сравнивать цифры по разрядам. А машина всегда должна сравнивать по разрядам. Поэтому для выяснения большего из двух чисел машине проще всего вычесть одно число из другого. По знаку разности ей будет ясно, какое число больше, какое меньше.
Приступим к составлению программы вычисления.
В ячейках оперативной "памяти" с № 1 по № 19 поместим команды. В ячейку № 20 - число а, в ячейку № 21 - число в, а ячейку № 22 оставим резервной. Вначале она будет пустой. Адреса ячеек запишем в десятичной системе счисления.
| - | № ячеек | Содержание ячейки |
|---|---|---|
| Ячейки с командами | 01 | Пс-20 |
| 02 | Ср-21 | |
| 03 | Ул-05 | |
| 04 | Ст | |
| 05 | Пс-20 | |
| 06 | Вч-21 | |
| 07 | Ус-13 | |
| 08 | Пч-22 | |
| 09 | Пс-20 | |
| 10 | Пс-22 | |
| 11 | Пч-20 | |
| 12 | Пк-01 | |
| 13 | Пс-20 | |
| 14 | Пч-22 | |
| 15 | Пс-21 | |
| 16 | Пч-20 | |
| 17 | Пс-22 | |
| 18 | Пч-21 | |
| 19 | Пк-01 | |
| Ячейки с числами | 20 | Число а |
| 21 | Число в | |
| 22 | 0 |
Проследим по таблице за работой машины. Нажатием кнопки она пущена в ход, и в управляющее устройство поступила команда из ячейки 01. В следующем такте команда будет выполнена. Число из ячейки 20, то есть первое число а, поступит в сумматор, предварительно поставленный на ноль, оно там и останется.
Затем в управляющее устройство поступит команда из ячейки 02. И число из ячейки 21, то есть число в, будет сравнено с числом а.
Второе указание алгоритма Эвклида будет выполнено.
Теперь в действие вступает условная команда, которая поступит в порядке очереди из ячейки 03. Управляющее устройство проверит результат предыдущей операции. Если числа окажутся равными, то последует команда из ячейки 04. Машина остановится. Числа равны, и каждое из них дает результат - общий наибольший делитель. Машина их потом напечатает - и задача решена.
Первая часть указания Эвклида выполнена.
Если же числа неравны, то согласно условной команде управляющее устройство обратится за следующим указанием к ячейке 05, потом к ячейке 06 и ячейке 07. И в соответствии с командами этих ячеек из числа а будет вычтено число в. И опять условная команда.
Если число в ячейке 20 меньше, чем число в ячейке 21, то условная команда 07 отошлет управляющее устройство сразу к ячейке 13. Последуют одна за другой команды 13, 14, 15, 16, 17, 18 и, наконец, 19. По ним числа айв обменяются местами. В ячейку 20 станет большее из них, а в ячейку 21 - меньшее. Так будет выполнено четвертое указание алгоритма Эвклида. И команда 19 снова отошлет управляющее устройство к первой ячейке. Цикл начнет повторяться.
Если же а больше в, то есть разность положительна, то в действие вступит следующая команда - из ячейки 08, затем 09, 10, 11 и 12. Проследим за этими командами. Команда 08 передает положительный остаток в свободную ячейку 22. Команда 09 пошлет число а в сумматор. Затем команда 10 погасит это число - оно нам больше не нужно - и пошлет в сумматор остаток из ячейки 22. Наконец команда 11 передаст остаток в ячейку 20.
Таким образом, в ячейке 20 вместо использованного числа а окажется остаток. А команда в ячейке 12 отошлет управляющее устройство снова к ячейке 01. Наконец выполнено и пятое указание Эвклида. И весь процесс начнет повторяться. Теперь в нем будут участвовать согласно алгоритму Эвклида вычитаемое и остаток. И так цикл за циклом будет идти процесс поиска наибольшего общего делителя, пока не возникнет равенство чисел в ячейках 20 и 21.
Итак, вся программа составляется всего из девятнадцати команд. Она пригодна для отыскания общего наибольшего делителя любой пары чисел. Количество команд останется всегда одинаковым.
Но общее число циклов повторения будет различным в зависимости от значения чисел а и в.
Нетрудно проверить, что если а=21, a в=14, то третий цикл приведет к отысканию общего наибольшего делителя, равного 7. А при многозначных числах циклов уже могут быть десятки и даже сотни.
Составление программ, особенно для сложных задач, - дело очень трудное. Здесь нужен большой опыт и высокая математическая квалификация.
На первых порах, когда электронные вычислительные машины только появились, приходилось затрачивать на программирование много времени. Несколько недель уходило на составление программы сложной задачи, которую машина после этого решала за несколько часов.
Но теперь процесс программирования сумели упростить и ускорить. Этого удалось достигнуть за счет различных усовершенствований.
Во-первых, составление программы частично поручают самой машине. Математик составляет руководство к действию в самом общем виде. А машина тщательно расписывает все команды и распределяет их по ячейкам. Составив для себя программу работы, машина затем по ней решает задачу.
Это уже напоминает порядок, которого придерживается при решении задачи человек. Он сначала составляет план решения: "в первом вопросе узнать то-то, во-втором найти то-то" и т. д. И уже затем по составленной "программе" производит вычисления и получает результат.
Во-вторых, по-мере эксплуатации машины накапливаются программы задач, которые приходится часто решать. Образуется своеобразная библиотека стандартных программ. И если по ходу дела нужно, например, извлечь квадратный корень, то уже не составляют каждый раз новую программу для извлечения корня, а используют ту, которая хранится в библиотеке программ.
И все-таки программирование отнимает пока еще сравнительно много времени. Поэтому, прежде чем поставить задачу для решения ее на машине, решают, выгодно это или нет. Ясно, что для простой задачи, да еще такой, которую приходится решать, может быть, всего один раз, электронную машину применять невыгодно. А для сложных массовых задач время, затраченное на программирование, полностью окупается. Даже с учетом этого времени результат получается в десятки и сотни раз быстрее, чем при решении их на ручных и счетно-перфорационных машинах.
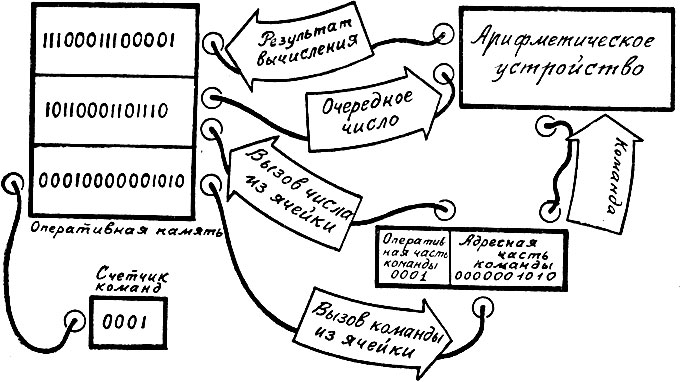
Управляющее устройство вызывает из оперативной 'памяти' команды и реализует их выполнение
На электронной вычислительной машине можно решить любую математическую или логическую задачу, для которой удается составить программу.
Состав операций бывает различным в разных электронных машинах. В мощных, универсальных их число доходит до тридцати-сорока. В специализированных, предназначенных для решения определенного класса задач число разных операций значительно уменьшено.
И построение команд бывает различным. Мы рассказали об одноадресной системе команд. Они так называются потому, что каждая команда содержит только один адрес.
Но бывает двух-, трех- и даже четырехадресные системы команд. В трехадресной команде содержится указание операции, которую нужно выполнить, адрес первого и адрес второго числа, участвующего в операции, и адрес ячейки, куда нужно послать результат.
Вот пример трехадресной команды. "Сложить число, находящееся в ячейке № 14, с числом в ячейке № 26 и отправить сумму в ячейку № 23". И все это записывается набором нолей и единиц. Набор получается, конечно, длиннее, чем набор для записи одноадресной команды. А в четырехадресную команду вводится еще один адрес - адрес ячейки, откуда нужно взять следующую команду.
Многоадресные команды сокращают размер программы, но усложняют устройства для их хранения и передачи. По-этому при создании машины и выборе системы команд принимают во внимание разные соображения и только после тщательного анализа останавливаются на том или ином принципе построения команд.
Наш рассказ об электронной вычислительной машине был бы неполным, если бы мы не попытались, хотя бы в самых общих чертах, объяснить, как взаимодействуют отдельные устройства машины, как происходит выбор команд из ячеек "памяти", их передача в управляющее устройство и их выполнение.
Очень трудно рассказать об этом подробно. Сотни каналов связывают части машины между собой. По ним в разных направлениях проносятся импульсы - управляющие, считающие, синхронизирующие - короткие и длинные, то следующие друг за другом с огромной частотой, то импульсы-одиночки.
Все они работают, каждый на своем участке, подчиненные единой цели.
Если бы мы с большой высоты посмотрели на тысячи поездов, бегущих в разные стороны по десяткам тысяч километров стальных путей, то увидели бы похожую картину. Беспорядочный на первый взгляд бег поездов подчинен единой цели, единому расписанию.
Перед нами блок-схема управляющего устройства электронной вычислительной машины. Оно связано со всеми частями многими каналами - линиями связи.
Основу управляющего устройства составляют счетчик команд и регистр команд. Машина, как мы уже говорили, работает отдельными тактами. В одном команда из оперативной "памяти" подается в управляющее устройство. Она фиксируется в регистре команд. А в следующем такте управляющее устройство реализует эту команду.
Счетчик аккуратно считает одну выполненную команду за другой.
Машина пущена в ход, и в счетчике команд появилось число 0001 - единица. Этот набор нолей и единиц открывает вентили ячейки № 1 оперативной "памяти". Хранящаяся там команда, изображаемая своим набором нолей и единиц, поступает в регистр команд. Такт выбора команды закончен.
Предположим, команда, попавшая в регистр, гласит: "Число в ячейке 10 сложить с числом, стоящим в сумматоре". В нашем коде, как мы знаем, это изображается четырнадцатиразрядным двоичным числом - 0001.0000001010.
Оперативная группа 0001, стоящая в регистре, пошлет сигнал "сложить" в арифметическое устройство. Тот самый сигнал, который в параллельном сумматоре действует на все магистральные вентили.
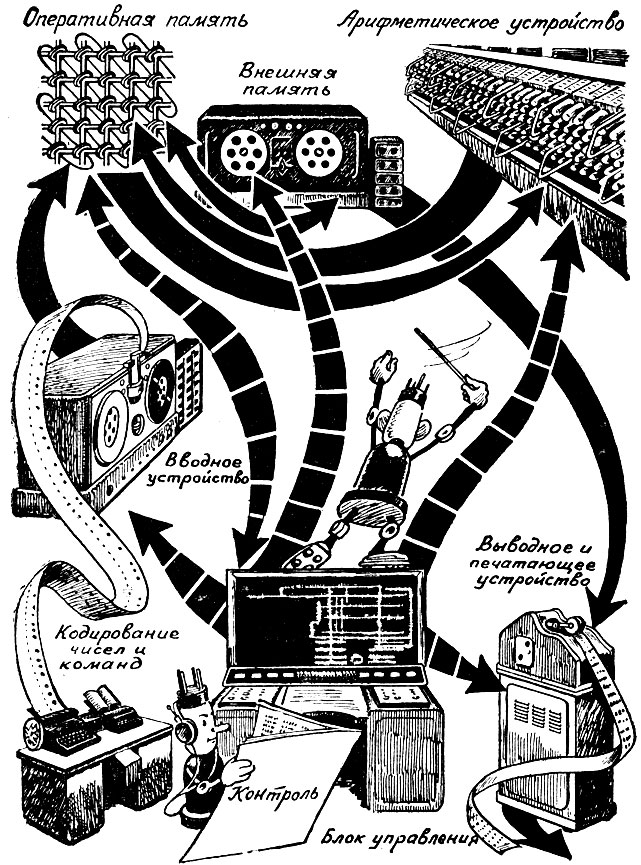
Блок-схема электронной быстродействующей вычислительной машины. Сплошные стрелы - путь чисел пунктирные - путь команд
А адресная группа 0000001010 откроет вентили ячейки № 10, и число из нее поступит в сумматор. Оно сложится с числом, которое там находилось. Такт реализации команды закончен. В счетчике команд появится цифра 0010 - два.
Теперь в следующем такте выбора команды откроются вентили ячейки № 2, и команда, стоящая там, заменит в регистре старую команду. Снова такт - выполнена и эта команда. Шаг за шагом, такт за тактом управляющее устройство будет выполнять команду за командой.
Если же в регистр попадет условная команда и сумматор выдаст сигнал "сумма отрицательная", то счетчик команд нарушит свой нормальный счет. В нем появится номер ячейки, указанный в адресной части условной команды. После ее выполнения порядковый счет команд возобновится и будет протекать до появления следующей условной команды. Так выполняется вся программа вычисления, реализуется машинное руководство к действию.
Слева вы видите блок-схему электронной вычислительной машины, характерную для большинства машин этого класса. На схеме показаиы пути прохождения чисел, над которыми производятся вычисления, и команд, управляющих работой всех устройств.
Все основные магистрали проходят через оперативный накопитель. Вначале сюда с перфоленты или перфокарт вводится программа вычислительного процесса, составленная из отдельных команд. А по первым командам в свободные ячейки оперативного накопителя с перфолент или перфокарт начинают поступать числа. Некоторые из них остаются в своих ячейках и сохраняют постоянное значение в течение всего вычислительного процесса. Они вступают в действие, когда, например, нужно умножить на постоянный множитель или прибавлять к результату вычисления постоянное число. Для других чисел оперативный накопитель служит как бы пересыльным пунктом. Через него они попадают во внешнюю память, чтобы вновь вернуться, когда в них возникнет необходимость, или тотчас же идут на переработку в арифметическое устройство. Окончательные результаты вычислений поступают в выводное устройство и печатаются на бумажных лентах или бланках установленной формы.
Электронная вычислительная машина замыкает длинную цепь всевозможных вычислительных машин, оперирующих с цифрами. Их так и называют цифровыми машинами. Они универсальны в полном смысле слова, ибо решение любой математической задачи, в какую бы первоначальную форму она ни была облечена, в конечном счете сводится к выполнению четырех арифметических действий.
Извлечение корней и интегрирование, простейшие задачи алгебры и сложные дифференциальные уравнения - все под силу электронному быстродействующему автомату.
Но автомат нуждается в программе, тщательно расписывающей последовательность выполнения всех операций. Ее составляет человек. Это он раскладывает сложнейшие математические задачи на простейшие арифметические действия, и даже в тех случаях, когда машина сама составляет для себя программу.
В вычислительной технике существуют и машины, работающие по другому принципу, принципу, не требующему замены сложных математических операций элементарными арифметическими. Об этих машинах теперь и пойдет у нас речь.
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'