Чтобы не искушать судьбу...

Сорок лет назад весь мир был восхищен необычайным мужеством и искусством русского летчика Нестерова.

Это и неудивительно! Совершить петлю, называемую "мертвой", на тихоходном и несовершенном самолете до Нестерова никто не решался. Даже считали это невозможным. И недаром среди многих телеграмм, полученных Нестеровым, была и такая, присланная инструкторами и летчиками Гатчинской авиационной школы:

"Приветствуем отважного товарища с мировым рекордом и убедительно просим не искушать судьбу вторично".

Еще большей отваги и мастерства требует высший пилотаж на мощных и сверхбыстрых реактивных самолетах. Попытайтесь представить себе, что такое скорость тысяча километров в час или триста метров в секунду! Здесь уже не секунды, а доли секунды имеют значение. Малейшая неточность в управлении самолетом, в его конструкции - и смертельная опасность нависает над пилотом.

Но советский летчик всегда уверен в совершенстве нашей авиационной техники. Ее творцы - ученые, конструкторы и рабочие - вложили огромный труд в создание самолетов, сочетающих превосходные летные качества и надежность в самых тяжелых условиях полета.

Проектирование и постройка современного реактивного самолета невозможны без глубоких и всесторонних теоретических исследований, расчетов и обширных экспериментов над моделями.

Сверхскоростной полет - сложный и многообразный динамический процесс. На него влияют различные факторы. Форма и размеры самолета, нагрузка, режим работы двигателей, устройство органов тяжести управления и даже шероховатость поверхности самолета.

Попытаемся несколько глубже проникнуть в закономерности динамического процесса полета.

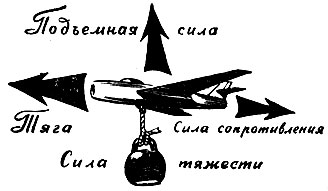
Система сил, действующих на самолет

Это, как, впрочем, и вся глава "Математическое зеркало", может показаться трудным для неподготовленного читателя. Здесь за простыми названиями - функция, интеграл, дифференциальные уравнения - и многими другими кроются сложные математические зависимости, составляющие основу вы сш ей м а тем а тики.

"Математическое зеркало" - это рассказ о вычислительных устройствах, основное назначение которых ускорить решение самых сложных задач высшей математики. Недаром их иногда образно называют "машинами с высшим образованием". Поэтому нет смысла рассказывать об этих машинах, не привлекая понятий высшей математики. К тому же было бы, по нашему мнению, неправильно тщательно обходить трудные вопросы, вместо того чтобы помочь читателю в них разобраться. Ведь в этом основное назначение книги.

Закономерности движения самолета в воздухе основаны на втором принципе Ньютона. Он, как известно, гласит: "Произведение массы тела на его ускорение в свободном движении равно сумме сил, действующих на тело".

Система сил, действующих на самолет, обычно сводится к четырем силам. Прежде всего это вес самолета с оборудованием, грузом, горючим. Его называют полетным весом, который нетрудно вычислить и даже измерить.

Второй силой является тяга мотора. Она и заставляет самолет двигаться. Сила тяги зависит от мощности двигателя, режима его работы, плотности воздуха и многих других факторов. Зависимость между ними устанавливают теоретическим путем и разнообразными экспериментами. Каждый новый тип двигателя испытывают при разных режимах работы, измеряют тяговую силу и выясняют влияние на нее тех или иных факторов.

Остальные две силы в системе имеют одинаковое происхо- : ждение. Своим существованием они обязаны воздуху.

Кто не испытывал на себе действие силы сопротивления воздуха - невидимого, но вечного врага всякого быстрого движения! Почти незаметная для медленно идущего пешехо* да, она становится весьма ощутимой для спринтера, пробе-* гающего сто метров почти за десять секунд. Еще сильнее ее чувствует гонщик на велосипеде или на мотоцикле.

Сила сопротивления воздуха очень быстро возрастает с увеличением скорости. А при движении со скоростью звука - 330 метров в секунду - она возрастает резким скачком. Для быстро летящего самолета сила сопротивления достигает огромной величины. Преодолеть ее способиы лишь тысячесильные двигатели.

Но сопротивление воздуха играет в авиации и полезную роль. Оно создает подъемную силу, уравновешивающую полетный вес. Каждый, кто в детстве запускал воздушного змея, хорошо знаком с действием этой силы. Без нее змей в воздух не поднимется.

Между продольной осью самолета и направлением его скорости существует небольшой угол - угол атаки. Он обеспечивает требуемую подъемную силу на крыльях самолета. Зависит она, как и сила сопротивления, от скорости полета и формы самолета.

Обе эти силы в авиации называют аэродинамическими.

Их невозможно определить чисто расчетным путем. На помощь ученым и конструкторам приходит модель.

Сколько приятных воспоминаний о детских годах, о дружной работе в пионерских кружках вызывает слово "модель"!

Можно ли забыть радостные минуты, когда построенная своими руками модель подъемного крана, автомобиля, катера занимает самое видное место в комнате? Или когда изящная ажурная модель самолета отрывается от земли и начинает плавно описывать круги в воздухе?

Пусть это только детская игрушка, лишь внешним обликом напоминающая могучую машину. Но немало выдающихся конструкторов, инженеров и смелых новаторов-рабочих начали с них знакомство с принципом действия и законами проектирования настоящих машин.

На выставке работ учащихся ремесленных училищ можно увидеть удивительные вещи. Миниатюрные модели станков, судов, зданий и даже атомной электростанции поражают точным воспроизведением геометрических пропорций, реальностью "натуры" до мельчайших деталей.

Но эти модели похожи на настоящие машины не только своим внешним видом, они действуют подобно настоящей машине и во многом повторяют ее рабочие функции.

"Детским" моделированием занимаются и взрослые ученые. Вот модель, точно воспроизводящая форму и размеры проектируемого самолета. На ней конструкторы изучают действие аэродинамических сил.

Модель помещают в аэродинамическую трубу, и в ней .происходит первая серия необычных полетов. Модель "летит", не двигаясь с места. Мимо нее с огромной скоростью проносится воздушный поток, созданный мощными вентиляторами, нагнетающими воздух в аэродинамическую трубу.

Модель рвется из удерживающих ее креплений. Они устроены так, что позволяют ей немного подвинуться, как бы уступая могучей силе воздушного потока. И воздушная нагрузка на модель передается рычажком специальным весам. Они "взвешивают" - измеряют силу лобового сопротивления и подъемную силу, испытываемые моделью. По ним ученые, пользуясь законами подобия, находят аэродинамические силы, действующие на настоящий самолет.

Подробно, всесторонне изучают конструкторы поведение модели в аэродинамической трубе. Меняют положение модели и скорость воздушного потока, форму и размеры крыльев, рулей и гондолы будущего самолета.

До 250 тысяч числовых показателей получают при испытании модели самолета в аэродинамической трубе. И тогда переходят к математическому анализу движения самолета.

Сила тяги, вес, лобовое сопротивление и подъемная сила определяют ускорение самолета, а значит, его скорость и траекторию полета. Эту зависимость называют уравнением движения самолета.

Решить это уравнение, рассчитать заранее траекторию полета было бы нетрудно, если бы действующие на самолет силы не изменялись во время полета - были постоянны. В действительности дело обстоит намного сложнее. Самолет попадает то в восходящие, то нисходящие потоки воздуха, его кидает из стороны в сторону, как корабль на волнах. Пассажиры из-за этого даже иногда страдают морской болезнью.

Устойчивое движение самолета обеспечивается рулями и элеронами, которыми управляет летчик или автопилот. Вот самолет попал в воздушную яму - его стремительно бросило вниз. Тотчас же органы управления выравнивают положение самолета в воздухе и снова возвращают на прежнюю высоту.

В полете непрерывно меняются и силы, действующие на воздушный корабль, и его положение в пространстве; все время работают органы управления. При движении самолета даже в малые доли секунды что-то и как-то меняется.

Самолет бросает из стороны в сторону, как корабль на волнах

И вот этот сложнейший динамический процесс, этот запутанный клубок, в котором переплетаются разнообразные явления, непрерывно изменяющиеся во времени, распутывается с помощью уравнений движения самолета. Они должны быть дифференциальными уравнениями, уравнениями, улавливающими малейшие изменения, происходящие в мельчайшие отрезки времени.

Само название этих уравнений происходит от слова "дифференциал", что означает разность, то есть разность между тем, что было, и тем, что есть, или между тем, что есть, и тем, что будет.

Только решив дифференциальные уравнения, можно заранее рассчитать, как будет меняться положение проектируемого самолета в пространстве, обеспечат ли органы управления устойчивое движение, не потеряет ли самолет скорость, сможет ли пилот безопасно выполнять фигуры высшего пилотажа.

Но все эти расчеты необычайно сложны. Подсчитано, что для решения математических задач, связанных с проектированием нового самолета, потребовалось бы десять тысяч вычислителей.

Как же быть? Ведь нельзя выпускать в полет машину, пока нет полной гарантии ее надежности. Нельзя послать летчика в воздух и разрешить ему полный опасности высший пилотаж, если нет твердой уверенности, что самолет выйдет из штопора, не врежется с огромной скоростью пикирующего полета в землю. Нельзя искушать судьбу!

И здесь на помощь конструкторам снова приходит модель. Но теперь это совсем особая модель - "математическое зеркало". Знакомство с ним начнем с простой алгебраической задачи. Вот ее условие:

a₁x₁+в₁х₂=с₁

а₂х₁+в₂х₂=с₂

Что оно означает?

Человек, не знакомый с математикой, вообще не сумеет ответить на этот вопрос. Математик даст самый общий ответ: "Это система из двух линейных алгебраических уравнений с двумя неизвестными. Но что именно она выражает, я сказать не могу". А инженеры разных специальностей скорее всего ответят так.

Инженер-электрик: "это уравнения напряжения или токов в электрической цепи с активными сопротивлениями";

инженер-механик: "это уравнения равновесия сил для системы рычагов или пружин";

инженер-строитель: "это уравнения, связывающие силы и деформации в какой-то строительной конструкции";

инженер-плановик: "это уравнения для расчета загрузки станков".

Пять человек по-разному ответили на один и тот же вопрос.

Кто же из них прав?

Как это ни странно - все! Каждый из ответов верен. Да, одна и та же система линейных алгебраических уравнений может отображать равновесное состояние и электрической цепи, и рычагов, и строительной конструкции.

Все зависит от того, что скрывается за постоянными коэффициентами а, в йен символами неизвестных - х₁ и х₂.

Инженер-электрик полагал, что постоянные коэффициенты - это величины активных сопротивлений, правые части- токи, питающие цепь, а неизвестными являются напряжения в узлах цепи.

Он хорошо знает, что цель, составленная из активных сопротивлений, линейная. В ней с нарастанием величины питающих токов пропорционально увеличиваются узловые напряжения. Следовательно, зависимость между токами и напряжениями в сложной электрической цепи описывается системой линейных алгебраических уравнений.

Инженер-механик считал, что постоянные коэффициенты - это упругости пружин, правые части - внешние силы, действующие на систему пружин, а неизвестные - величина их деформации. И такая механическая система является линейной. Чем больше внешняя сила, тем больше сжатие или растяжение пружины. Значит, зависимость между силами и деформациями пружины в сложной упругой системе тоже описывается линейными алгебраическими уравнениями.

Инженер, планирующий производственный процесс, не без основания думал, что написанные уравнения имеют прямое отношение к его специальности. Нужно рассчитать размеры двух партий деталей. Каждая деталь обрабатывается сначала на одном, затем на другом станке. И эта задача сводится к решению тех же двух уравнений. Но теперь постоянные коэффициенты первого уравнения - это время обработки одной детали из каждой партии на первом станке, правая часть его - общее заданное время работы первого станка, а неизвестные -искомое число деталей в каждой из двух партий.

Таким же образом составлено второе уравнение - для обработки деталей на втором станке.

Вот почему математик дал такой неконкретный ответ.

Он знает, что статические явления в любой физической системе: электрической, механической, гидравлической, тепловой, акустической, экономической - описываются алгебраическими уравнениями первой степени.

Как видите, каждый действительно оказался по-своему прав!

"Казалось бы, что может быть общего между расчетом движения небесных светил... и качкой корабля... - говорил знаменитый русский ученый академик А. Н. Крылов. - Между тем, если написать только формулу и уравнения без слов, то нельзя отличить, какой из этих вопросов решается: уравнения одни и те же".

'Казалось бы, что может быть общего между качкой корабля и движением небесных тел...'

И в этом поразительном математическом сходстве различных явлений кроются огромные возможности для создания удивительного мира математических моделей. Внешне они не имеют даже отдаленного сходства с "натурой". Но в этих моделях, как в волшебном зеркале, отражаются внутренние закономерности моделируемого явления. Их роднит с "натурой" общая математическая зависимость. Процессы в модели и в "натуре" описываются одинаковыми уравнениями.

Таков закон природы.

Владимир Ильич Ленин писал: "Единство природы обнаруживается в "поразительной аналогичности" дифференциальных уравнений, относящихся к разным областям явлений".

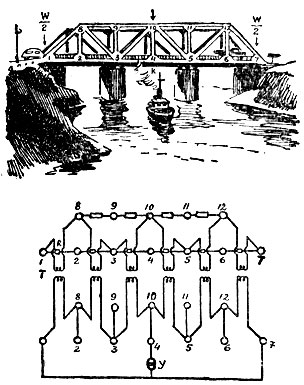
Электрическая цепь моделирует форму моста

В проектном бюро разрабатывается новая строительная конструкция. Для ее расчета нужно решить систему из десяти линейных алгебраических уравнений.Уже одно это требует довольно много времени. Но для правильного выбора конструкции необходимо проверить несколько различных вариантов. Объем вычислительной работы резко возрастет. И тогда на помощь приходит математическая модель.

Электрическая цепь, составленная из активных сопротивлений, моделирует эту строительную конструкцию. Величины сопротивлений выбирают соответственно коэффициентам упругости ее деталей.

К цепи подводят токи, пропорциональные нагрузкам на конструкцию, в узлах цепи измеряют напряжения, пропорциональные деформациям. Их-то и надо было вычислить проектировщикам. Для этого составлялась система уравнений, в которой деформации были искомыми неизвестными.

Электрическая цепь решила эту систему уравнений без вычислений. Они заменены измерением напряжений.

Измерение вместо вычислений. Что может быть проще и быстрее! Во много раз сокращается время решения задачи и тем самым время проектирования новой конструкции.

А чтобы рассчитать другой вариант, нужно только изменить величины сопротивлений. Новое измерение - и ответ готов! Ту же задачу проектировщики могли решить на гидравлической, тепловой, механической, акустической модели, используя математическое "однообразие" разнообразных процессов. Но трудно придумать что-либо удобнее электрической модели.

Электрические токи распространяются мгновенно. Для электрической модели не нужны резервуары, сложные детали, высокие температуры, мощные источники звука.

Электричество отражает все многообразие явлений в природе, все законы можно выразить на языке электричества. Даже состояние человека наиболее верно и точно определяется явлениями чисто электрическими: электрокардиограмма характеризует работу сердца, а электроэнцефалограмма - работу мозга.

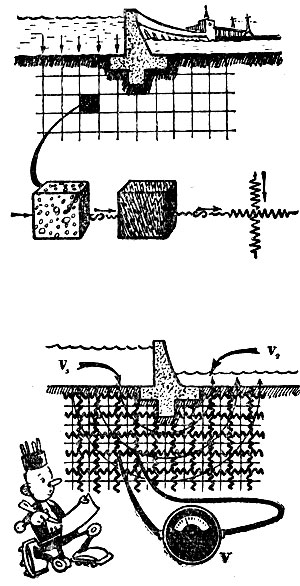
Электрическая модель плотины. С помощью электромодели изучают просачивание воды под плотиной

И то и другое представляет собою запись кривых линий на фотобумаге. Точно такие же кривые можно было бы получить, если бы приборы записывали не токи сердца и мозга, а токи, возникающие в электрических цепях, созданных руками человека.

Ферма моста, на которую действует множество разных сил, может быть заменена механической моделью. Но можно создать и ее электрическую модель.

Механическая сила, действующая в самой опасной точке, где приложена максимальная нагрузка, заменяется силой электрического тока.

Изучая плотину, вместо ее точной модели и воды можно воспользоваться электрическим током, а вместо сооружения реального подобия плотины соединить несколько катушек проволоки.

На заре завоевания электричества ученые, не знавшие всех его тайн, старались их раскрыть, устанавливая сходство электрических процессов с явлениями гидравлическими, тепловыми и механическими.

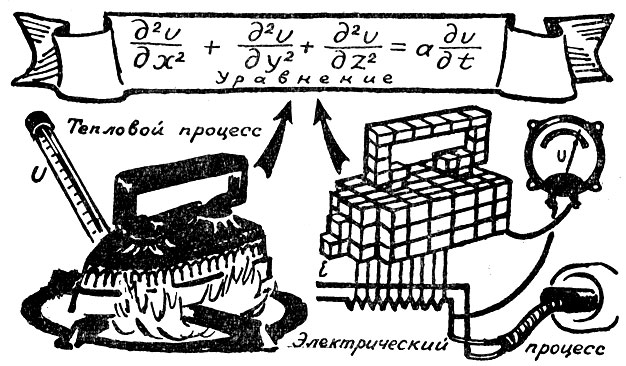
Аналогия между тепловыми и электрическими процессами позволяет моделировать распределение тепла в телах самой сложной формы

Эти совсем, казалось бы, не похожие физические процессы они всеми силами пытались привести к единым математическим законам. И, естественно, для объяснения пользовались тем, что знали, к чему привыкли.

Так возникла аналогия между течением воды в трубах и движением электричества в проводах, распространением тепла и распределением электрических напряжений, колебаниями в механических и электрических цепях.

Сейчас электричество сделалось таким же привычным, как вода и тепло. Электрооборудование стало простым, надежным. Появилась и достигла большого развития электронная техника.

Ни одна отрасль человеческого знания не располагает теперь столь совершенной, точной и чувствительной измерительной аппаратурой, как электротехника и электроника. И стало возможным с помощью электричества и электрических моделей изучать все другие явления.

...Группа людей с напряженным вниманием смотрит на экран электронного осциллографа. На его матово-белой поверхности медленно проплывает светящаяся точка. Она оставляет за собой след - тонкую изумрудного цвета змейку причудливой формы. Это... траектория летящего самолета.

"Летные" испытания проектируемого самолета идут полным ходом. Их программа обширна и многообразна. Исследуется влияние силы тяги и полетного веса на размеры и форму несущих поверхностей. Изучается реакция воображаемого самолета на действия летчика.

Параметры самолета, движение рулей, режимы работы двигателей вводятся в моделирующую установку, и светящаяся точка тотчас же изменяет свой путь на экране осциллографа.

"Математическое зеркало" быстро и безошибочно отображает самые рискованные эволюции самолета в воздухе, самые сложные фигуры высшего пилотажа. За несколько десятков минут испытано множество вариантов конструкций и режимов полета еще не построенной машины. В проект внесены необходимые исправления - надежность и безопасность полета будущего самолета обеспечены.

'Математическое зеркало' быстро и безошибочно отображает самые рискованные эволюции самолета в воздухе

Без математического моделирования на решение дифференциальных уравнений и анализ всех вариантов нужно затратить много времени, даже используя быстродействующую цифровую машину. А самое главное, необходимы опасные для жизни пилота разнообразные летные испытания в "натуре" - на реальном самолете.

"Новое дело - всегда риск" - эти слова приобретают особое значение, когда речь идет об испытании нового самолета. Оно всегда сопряжено с неожиданными для испытателя случайностями.

Математическая модель перенесла полный опасности испытательный полет из безграничных воздушных просторов в стены лаборатории. Точный расчет и проникновение "математического зеркала" в закономерности полета исключают "риск нового".

Поэтому спокойно садится летчик в кабину нового самолета, уверенно выполняет самые сложные фигуры высшего пилотажа. Он знает: ему не угрожает неизведанный случай, ему не нужно искушать судьбу.