Командует модель

Темная августовская ночь наступила незаметно и словно черным покрывалом окутала улицы прифронтового города К. Ни единый луч света не пробивается сквозь плотно закрытые шторами окна. И только где-то высоко в небе чуть-чуть заметно мигают одиночные звезды. Казалось, глубокий сон охватил этот небольшой городок, только накануне освобожденный нашими войсками в их стремительном наступлении на запад.

Но в штабе противовоздушной обороны, размещенном неподалеку от центральной площади, окруженной старинными зданиями, кипит напряженная работа.

Авиация противника пытается нанести бомбовый удар по коммуникациям советских войск. Любой ценой разрушить мост и железнодорожный узел в северо-восточном предместье города - таков категорический приказ гитлеровского командования.

Поразить быстро летящий самолет значительно труднее, чем подстрелить утку

В штаб и на командные пункты зенитных батарей, полукольцом окружающих город, только что поступило донесение: "Воздух".

Пароль "Воздух" обеспечивает передачу сообщения по телефону вне всякой очереди. Допустим по линии связи поступили сведения, что в одном из районов обнаружено 12 самолетов Ю-88, идущих курсом 35° на высоте 30 гектометров (3000 метров). Самолеты прошли над наблюдательным пунктом в 23 часа 46 минут .

Поразить быстро летящий самолет значительно труднее

В черноту ночи врезались, подобно сверкающим иглам, прямые лучи яркого света. Длинные щупальца прожекторов деловито зашарили по небу, то собираясь вместе, как будто для короткого совещания, то вновь разбегаясь каждая по своим делам.

Внезапно одно из щупалец сменило свой стремительный бег на еле-еле заметное движение. В яркий столб света попалась сверкающая точка. Ослепленный мощным лучом2 летчик вражеского самолета отчаянно рвется прочь от опасности. Но тщетно!

Поразить быстро летящий самолет значительно труднее

К лучу со всех сторон спешит помощь. И вот уже не одно, а три-четыре щупальца охватывают Самолет с обезумевшим от страха экипажем и неотступно сопровождают его до момента роковой встречи с несущим смерть зенитным снарядом.

Далеко внизу, на земле, притаились смутно поблескивающие в темноте дула зенитных пушек. Точно и быстро работают наводчики у прибора управления зенитной стрельбой.

Раздается команда: "По самолету - 36". Ее повторяет командир приборного отделения, и через несколько секунд звучит ответ: "Цель поймана".

Направленные с "земли оптические трубы медленно поворачиваются, следуя за освещенным самолетом.

Механизмы и электрические цепи прибора управления непрерывно решают математическую задачу "встречи" - вычисляют точку, куда следует послать снаряд, чтобы он встретил вражеский самолет.

Бесшумно поворачиваются длинные жерла пушек, послушные указаниям прибора управления. Оглушительно-отрывисто один за другим раскалывают тишину выстрелы. Сверкает в небе точка, вспыхивает ярким огоньком, и падающей звездой самолет стремительно летит вниз.

Короткое, но ожесточенное сражение зенитной артиллерии с авиацией закончено. Немногословно и суховато рассказывает боевое донесение штаба противовоздушной обороны о полных опасности и напряжения минутах, о провалившейся попытке врага и о потерянных им в бою самолетах.

В стихах, повестях и романах ярко запечатлены боевые эпизоды Великой Отечественной войны, отвага и искусство советских воинов.

И, наверное, еще много волнующих произведений будет написано на эту тему.

Наша задача более скромная.

Каждый хорошо знает, как трудно стрелять по движущейся цели. Очень многие без промаха поражают неподвижную мишень. Но редко кому удается сбить быстро летящую утку. Чаще всего это случается в охотничьих рассказах.

Чтобы попасть даже с небольшого расстояния в подвижную цель, нужно не только хорошо владеть искусством стрельбы, но учитывать многие обстоятельства.

А теперь попытайтесь представить себе, насколько сложно обеспечить попадание снаряда в сравнительно небольшой по размерам самолет, летящий со скоростью 200 - 300 метров в секунду на высоте 8 - 10 километров. Это намного труднее, чем попасть крошечной дробинкой в муху, пролетающую от вас на расстоянии десяти метров.

Не легче попасть в небольшую цель и бомбой, сброшенной при тех же условиях с самолета. Прицельное бомбометание - сложный процесс. Чтобы его успешно осуществить, нужно произвести много различных измерений и расчетов.

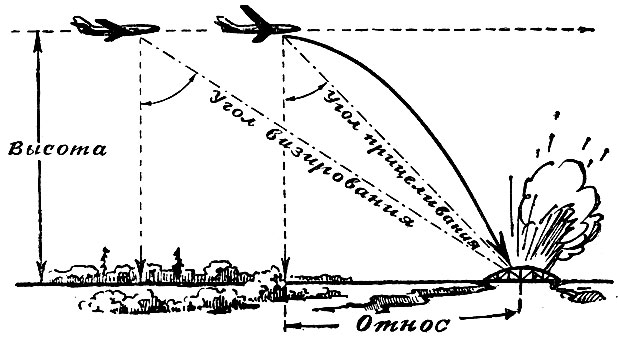
Когда угол визирования на цель станет равным углу прицеливания, с самолета сбрасывается бомба

Перед нами рисунок, на котором изображен самолет, направляющийся к мишени, чтобы сбросить на нее бомбу. Где же нужно это сделать, на каком расстоянии от цели, чтобы точно в нее попасть?

Ясно, не прямо над целью. Ведь бомба сбрасывается с летящего самолета, а не с аэростата, неподвижно висящего в воздухе над целью. Поэтому она будет падать не вертикально, а по кривой линии, близкой к параболе.

Пока бомба долетит до земли, она сместится относительно точки бросания также и по горизонтали. Это смещение называют относом. Он зависит от высоты и скорости самолета в момент сбрасывания бомбы, а также от баллистических свойств самой бомбы.

Бомбардир всегда имеет в своем распоряжении таблицы для бомбометания. В них он находит величину относа и время падения бомбы в зависимости от ее типа, высоты и воздушной скорости полета, указываемых навигационными приборами. И если, например, самолет летит на высоте 4 тысяч метров со скоростью 380 километров в час, то по таблице он сразу найдет, что относ составит около 2 400 метров.

Теперь ясно, что если нет ветра, то бомбу нужно сбросить с самолета в тот момент, когда он будет находиться на расстоянии 2 400 метров от цели.

Но как найти точку сбрасывания бомбы в огромном воздушном пространстве, притом находясь на борту быстро летящего самолета? Оказывается, проще всего это сделать, определив угол прицеливания, то есть угол, под которым цель видна с самолета в момент бросания бомбы.

Находят его так. При полете на боевом курсе бомбардир через оптическую трубу неустанно ведет наблюдение за целью. По мере приближения к ней ему приходится все время трубу поворачивать.

В тот момент, когда угол между трубой и вертикалью совпадает с углом прицеливания, бомбардир нажимает кнопку бомбосбрасывателя. Бомба отрывается от самолета и летит на цель.

Проследим теперь за всеми операциями, которые нужно выполнить, чтобы правильно сбросить бомбу.

По приборам надо определить высоту и воздушную скорость полета. Найти по ним в таблице величину относа. По этим данным вычислить угол прицеливания, для чего величина относа бомбы делится на высоту. При этом получается еще не угол прицеливания, а только его тангенс. По нему бомбардир должен найти угол прицеливания и установить его на прицеле.

Все это нужно сделать за несколько секунд, пока самолет идет на боевом курсе. К тому же в эти короткие секунды зенитная артиллерия ведет стрельбу с особой силой. Во время полета на боевом курсе легче всего сбить самолет. Он летит прямолинейно и равномерно и не должен производить маневров, чтобы уйти от снаряда. Малейшее отклонение от курса, незначительная ошибка в расчете - и бомба упадет далеко от цели. Боевое задание не будет выполнено! Поэтому все операции, о которых мы рассказали, нужно делать быстро и безошибочно.

Но работа бомбардира усложняется еще и тем, что во время бомбометания почти всегда дует ветер: встречный, попутный или боковой. Если его скорость равна хотя бы пяти метрам в секунду, то бомбу отнесет от цели еще на 140 метров. С таким промахом нельзя не считаться!

Найти прицельный угол с учетом ветра намного труднее. Приходится за какие-то секунды вычислять сложную функцию, умножать и делить.

Ясно, что для таких расчетов невозможно пользоваться арифмометром или любой другой механической цифровой машиной. Все равно не хватит времени на решение задачи.

Нужно устройство, которое давало бы ответ мгновенно и освобождало бомбардира от всяких вычислений. Это делает математическая модель. Она быстро и надежно решает задачу прицеливания. Будем знакомиться с моделью по частям.

Вот тангенсный механизм. Всего два стержня - один качается на шарнире, а другой движется поступательно. Стержни соединены "ползушкой".

Воспользуемся этим механизмом для вычисления угла прицеливания. Поставим стержень, двигающийся поступательно, так, чтобы он смоделировал, то есть представил в каком-то масштабе, величину относа. А расстояние по вертикали между опорами стержней установим в том же масштабе пропорционально высоте бомбометания. Это делают по специальным шкалам.

Как только выполнены несложные операции, качающийся стержень станет под углом прицеливания, который можно отсчитать по шкале.

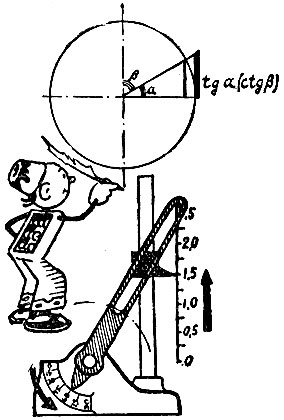
Тангенсный механизм

Простая модель дает ответ значительно быстрее, чем арифмометр. Большая скорость работы - основное преимущество моделирующих устройств по сравнению с цифровыми вычислительными машинами.

Цифровые машины, как уже читатель знает, производят вычислительные операции непосредственно над многоразрядными числами. Машина складывает, вычитает, умножает и делит числа по законам арифметики,

И если мы хотим с помощью арифмометра найти сумму двух меняющихся слагаемых, то каждое из них нужно задавать в виде конкретных чисел. А раз слагаемые все время меняются, то, значит, их будет много. И придется каждую пару чисел вводить в арифмометр и складывать. Труд тяжелый!

В моделирующих устройствах математические величины изображаются не конкретными скачкообразно меняющимися числами, а воспроизводятся непрерывно изменяющимися физическими величинами.

Представьте себе два сосуда. В один вода поступает капля за каплей, а в другой льется непрерывной струйкой. Первый наполняется скачкообразно - дискретно, второй непрерывно.

В арифмометр числа поступают по единицам, "по капле", счетчик "наполняется" скачкообразно. Он показывает: 1, 2, 3, 4 и т. д.

В моделирующее устройство число, отождествляемое физической величиной, втекает непрерывно, как струя воды.

В тангенсном механизме физическими величинами являются перемещения стержней. Этот механизм не вычисляет, а именно воспроизводит - моделирует функции тангенса.

А вот механизм, который моделирует процесс суммирования непрерывно меняющихся слагаемых. В нем и слагаемые и сумма воспроизводятся тоже механическими перемещениями стержней. Стержни нужно передвигать в соответствии с изменением слагаемых.

Нетрудно заметить, что при этом перемещение средней точки перекладины равно полусумме перемещения стержней. Механизм из реек и шестеренок удваивает это перемещение и непрерывно выдает сумму непрерывно изменяющихся слагаемых.

Обе модели механические. Но мир подобия велик. Многообразны средства моделирования. И ученые умеют находить в этом мире "разные одинаковости".

Тот же самый процесс суммирования может выполнять не механизм, а электрическая цепь.

Она складывает электрические токи, которые вырабатывают два источника. Один дает ток, пропорциональный первому слагаемому, другой - второму.

Ток в узловой точке, куда поступают токи от источников, будет равен сумме слагаемых. Так электрическая цепь моделирует сложение двух непрерывно меняющихся математических величин.

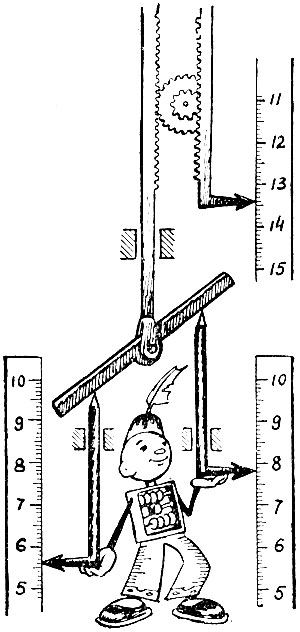
Слагаемые вводятся перемещением боковых стержней. Верхний стержень показывает сумму

Сколько времени нужно потратить на умножение с помощью арифмометра двух многозначных чисел? По край ней мере полминуты. Нужно установить множимое, а затем вертеть ручку столько раз, сколько единиц в цифрах множителя. При множителе, равном, например, 679, это придется сделать 22 раза. Сначала умножить на 9 единиц, потом на 7 десятков и, наконец, на 6 сотен. Кроме того, после умножения на каждый разряд нужно сдвигать каретку. Такую процедуру придется выполнять для каждой пары чисел, если мы хотим найти произведения, где каждый сомножитель принимает различные значения.

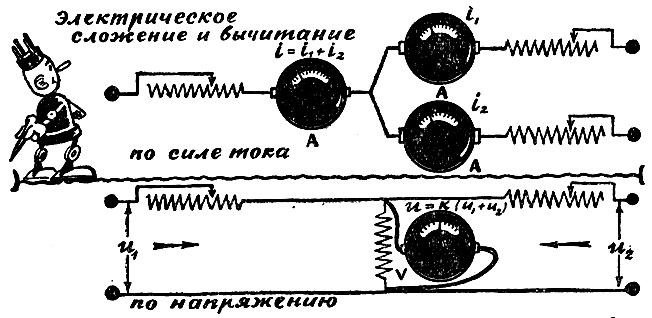
Устанавливая токи, или напряжения - слагаемые, сразу же на приборе получают ток или напряжение - сумму

А теперь посмотрите, как Электрическое легко эта зависимость моделируется с помощью простого механизма. Он состоит всего из двух колес - диска и ролика. Они прижаты друг к другу с помощью пружины. Если вращать диск, то благодаря трению будет вращаться и ролик.

Это фрикционная передача. Она обладает интересным свойством. Скорость вращения ролика зависит от его расстояния до центра вращения диска.

Поставьте ролик так, что бы это расстояние равнялось его радиусу. Тогда при одном

обороте диска ролик повернется тоже на один оборот. Если расстояние увеличить, ролик повернется на больший угол, чем диск. И наоборот, если расстояние уменьшить, уменьшится угол поворота ролика.

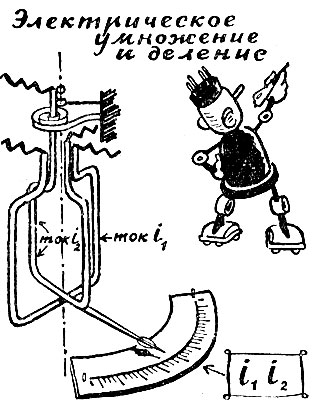
С помощью ваттметра можно умножать и делить токи, подаваемые в катушки прибора

Угол поворота ролика пропорционален его расстоянию до центра диска и углу поворота диска. Он дает произведение этих двух величин.

Чтобы умножить с помощью фрикционного механизма, нужно сдвинуть ролик на величину, пропорциональную первому сомножителю, а диск повернуть на угол, пропорциональный второму. Поворот ролика даст произведение. Оно получается намного быстрее, чем в арифмометре.

Фрикционный механизм

Читатель, вероятно, обратил внимание, что, рассказывая о работе моделирующих устройств, мы все время употребляем слово "пропорционально". Это не случайно.

В небольшом тангенсном механизме невозможно отложить 2400 метров относа или 4 тысячи метров высоты.

Электрическая цепь, моделирующая сложение сил, в действительности складывает не килограммы, а амперы.

При моделировании математическую и физическую величины связывает масштаб - коэффициент пропорциональности. Он переводит математическую величину на "язык" модели.

"Все это так, - скажет каждый, познакомившись с простыми и очень удобными математическими моделями. - Они действительно имеют преимущества перед цифровыми машинами в скорости работы. Но как же обстоит дело с точностью?"

Если -на арифмометре сложить два числа, например 73,8 и 13,6, то мы получим 97,4. И так при любом числе разрядов в слагаемых. Ответ всегда будет точен. А при сложении на моделирующем устройстве неизбежна ошибка. Прежде всего по шкалам невозможно абсолютно точно установить слагаемые, особенно многоразрядные. Нельзя также выполнить абсолютно точно размеры механизма или параметры электрической цепи. Они будут отличаться от норм.

Представьте себе, что в механическом суммирующем устройстве расстояния между стержнями не равны в точности друг другу. Тогда перемещение верхнего стержня уже не будет равно сумме перемещений боковых стержней. И если сложить наши два числа, то получим или 97, или 98, или даже число, еще более неточное.

Действительно, цифровые машины работают значительно точнее, чем моделирующие. Они позволяют получать результат с какой угодно точностью. А моделирующие устройства всегда дают ошибку в пределах от 0,1 до 10 процентов точного значения. Величина ошибки зависит от качества изготовления модели, от физического принципа, на котором она строится, и многих других причин.

Точнее работают механические модели, менее точно - электрические. При современных технических средствах не удается добиться точности свыше 0,01 процента.

Выигрыш в скорости всегда приводит к потере в точности. И наоборот. В вычислительной технике это неизбежно. И борьба между скоростью и точностью привела к развитию двух основных типов вычислительных устройств - цифровых и моделирующих.

Вы уже знаете историю зарождения и развития механических и электромеханических цифровых машин. Еще в прошлом столетии они получили признание, как незаменимое средство для механизации бухгалтерских, финансовых и экономических расчетов. Ведь их нужно производить абсолютно точно - учитывать даже копейки.

"Без копейки рубля не бывает", - любят говорить бухгалтеры. И когда многомиллионный баланс не сходится даже в копейках, то он подвергается самому внимательному и пристрастному контролю.

Длительное время цифровые машины (до появления быстродействующих) не привлекали к себе особого внимания математиков. Для решения с их помощью сложных задач нужно было разрабатывать специальные алгоритмы. А вычисления требовали очень много времени. И ученые упорно искали более удобные вычислительные средства.

Тогда появились математические модели. Вначале это были самые простые механические устройства, получившие название математических инструментов. Они служили для измерения площадей, длин кривых, вычерчивания и анализа различных сложных графиков. Затем появились и более сложные математические приборы. Но их производство при тогдашнем уровне техники было делом очень трудным. Нужна была высокая техническая культура и точность изготовления. Поэтому создание моделирующих устройств шло медленнее, чем цифровых.

Дальнейшему развитию и промышленному производству математических моделей во многом способствовало то, что они оказались самым эффективным средством для бомбо- и торледометания, зенитной и воздушной стрельбы морской и береговой артиллерии. Высокая скорость работы ставила их вне всякой конкуренции. Да и получаемая точность решения была вполне достаточной для "боевых" вычислений.

Моделирующие вычислительные устройства быстро совершенствовались. Появились электромеханические, электрические 'и электронные модели.

И даже теперь, когда в вычислительную технику гигантскими шагами вступили электронные цифровые машины, моделирующие системы прочно сохраняют свое место в арсенале вычислительных средств, в том числе и военных.

Современный бомбардировщик - это своеобразный воздушный вычислительный центр. В нем есть бомбардировочный прицел - очень сложный автомат для вычислений. Высота и воздушная скорость самолета вводятся в него автоматически. Прицелы снабжаются радиолокаторами. Помимо прицела бомбометания, есть прицел воздушной стрельбы, с помощью которого ведется обстрел атакующих самолет 'истребителей. Установлены вычислительное устройство для решения навигационных задач и многие другие аппараты, контролирующие полет и управляющие им.

Но за самолетом, атакующим цель, неотступно наблюдает другой вычислительный центр. Далеко внизу на земле оптические трубы или радиолокаторы синхронно поворачиваются, следя за бомбардировщиком, легшим на боевой курс. Измеряются его скорость, направление полета, высота и дальность. По ним вычислительное устройство решает задачу прицельной зенитной стрельбы.

За время полета зенитного снаряда самолет пролетит какое-то расстояние. Значит, нужно целиться не в самолет, а в точку, где он будет через некоторое время, - это вычисляет математическая модель. Она же автоматически посылает зенитный снаряд в точку встречи его с самолетом.

В ожесточенной борьбе авиации с зенитной артиллерией побеждают мастерство и отвага человека и совершенство боевой техники, в которой немаловажную роль играет математическая модель.

Желаете заниматься трахом в обществе разной шлюхи? Портал prostitutkicheboksaryxxx.info призывает попользоваться услугами рискованных индивидуалок, которые готовы даже на опыты в .