Трение и емкость решают задачи

Признаемся, мы умышленно отодвигали самое трудное все дальше и дальше. Однако пришло время, и мы вынуждены начать рассказ о самом сложном.

В книге уже неоднократно упоминалось о функциях и бесконечно малых величинах, об интегралах и дифференциальных уравнениях. Но дальше упоминания дело не шло. Теперь нужно не только раскрыть эти понятия, но и показать, как машина интегрирует и решает дифференциальные уравнения.

Великий Эйлер утверждал, что основы дифференциального и интегрального исчисления может усвоить даже десятилетний ребенок, обладающий здравым смыслом.

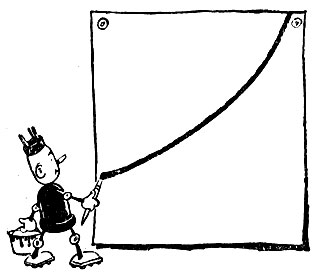
Нужно проинтегрировать функцию, заданную кривой, в пределах ширины страницы

Нет сомнения в том, что гениальный ученый действительно мог бы рассказать об этих трудных вещах так, чтобы их понял и ребенок. Но мы в этом рассказе, больше чем когда-либо, вынуждены рассчитывать на здравый смысл читателя, чем на собственные силы.

Ваш взгляд скользит по строчкам этой страницы. Отвлекитесь ненадолго от чтения и вычислите площадь, занятую текстом. У вас, вероятно, получилось около 180 квадратных сантиметров. Что же вы сделали? Не подозревая, произвели операцию интегрирования.

Но этот пример скорее привлечен для успокоения читателя, чем для пояснения самого процесса интегрирования. Не все так просто, как может показаться при вычислении площади этой страницы.

В самом деле. Разделите эту страницу на две части кривой линией так, чтобы она прошла от нижнего левого угла и до верхнего правого, и определите площадь ее нижней части. Вы убедитесь, что элементарными приемами это сделать невозможно. Нужно проинтегрировать функцию, заданную кривой, в пределах ширины страницы.

Мы облекли последнюю фразу в точную, хотя, наверное, не всем понятную математическую форму. Попытаемся сделать ее понятной.

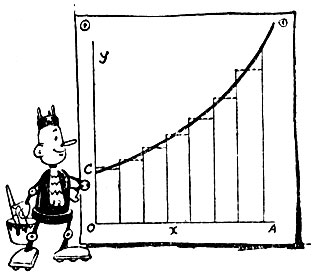
Площадь, расположенную под кривой, можно вычислить приближенно, разбив ее на прямоугольники

Расположим на рисунке прямоугольник, изображающий страницу, между двумя прямыми линиями - горизонтальной и вертикальной. В математике их называют осями координат.

На другом рисунке в такой же системе координат представим нижнюю часть страницы, расположенной под кривой линией. Теперь сравним оба рисунка.

На первом - площадь ограничена сверху прямой линией, параллельной горизонтальной координатной оси. Обратите на нее внимание.

Отметим на этой прямой какую-нибудь точку. Ее координаты - расстояния до обеих осей по перпендикулярам.

Не трудно заметить, что для разных точек этой прямой горизонтальная координата меняется, а вертикальная - остается постоянной.

На втором рисунке дело будет обстоять сложнее. Здесь площадь ограничена кривой линией. И для разных точек ее меняется значение обеих координат.

Форма кривой имеет важное значение. Посмотрите на рисунок. Чем больше горизонтальная координата, тем больше и вертикальная. Кривая определяет зависимость между ними, то есть вертикальная координата у зависит от горизонтальной координаты х.

Математики в таких случаях говорят: у есть функция от х.

Мы в этой книге иногда, правда очень редко, пользуемся математическими символами, уравнениями и формулами. Может быть, это кому-либо покажется неуместным в простых рассказах и очерках о науке. Таким читателям напомним об одном письме к Фарадею английского физика Томсона (о нем рассказ впереди). Он писал, что не мог понять содержания одной статьи, так как "она не оживлена х-ми и у-ми".

Под математической функцией следует понимать закон, управляющий взаимными зависимостями переменных величин.

Изучением функций занимается большинство математических дисциплин. Это и понятно! Ведь все явления в окружающем нас мире находятся во взаимосвязи и так или иначе влияют друг на друга. С той или иной точностью эти связи можно представить в виде функциональных зависимостей, иногда простых, иногда очень сложных. А это позволяет использовать могучий аппарат математики для исследования и управления процессами в живой и неживой природе.

Поэтому математики упорно изучают свойства различных функций, ищут все новые виды функциональных зависимостей, развивают и совершенствуют методы теории функций для решения практических задач.

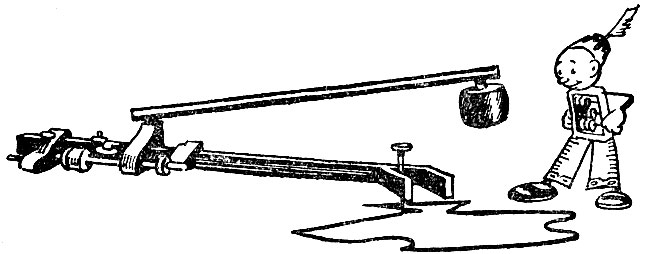
Таким простым прибором планиметром - можно измерить площадь, ограниченную самой замысловатой кривой

Вернемся теперь к вычислению площади нижней части страницы. Каким же способом ее найти?

Из школьного курса геометрии мы знаем формулы для подсчета площади прямоугольника и треугольника. Этими формулами можно пользоваться и для вычисления площади любой фигуры, ограниченной прямыми линиями. Ее всегда можно разбить на несколько треугольников. Мы умеем также вычислить по формулам площадь круга или его части.

Но как вычислить площадь, ограниченную любой "бесформенной" кривой? Ведь такая площадь не может быть разбита на прямоугольники и треугольники, для ее вычисления нет простой и точной математической формулы.

Ответ на этот вопрос дает высшая математика. Одно из главных ее достижений - создание общего метода решения подобных задач. Это метод интегрирования.

Попробуем вначале вычислить приближенно площадь, расположенную под кривой линией. Для этого разделим всю ширину страницы на некоторое число равных участков. Восстановим из каждой точки деления перпендикуляр до кривой., Получим ряд площадок. Они ограничены сверху кусочками кривой. Заменим кусочки кривой прямолинейными отрезками.,

Сумма полученных таким образом прямоугольных площадок и даст приближенное значение всей площади, расположенной под кривой линией.

Ее можно вычислить точнее. Для этого надо сделать прямоугольники более узкими: их число увеличится.

Вспомните, как знаменитый узбекский математик Гияс-ад-Дин Джемшид нашел число π. Он вписал в окружность с радиусом, равным единице, правильный многоугольник и увеличивал число его сторон, пока не дошел до астрономической цифры - более восьмисот миллионов.

Джемшид нашел площадь этого круга с точностью до шестнадцати знаков. А площадь круга с радиусом, равным единице, как раз равна тс.

И в нашей задаче площадь можно вычислить с какой угодно степенью точности, увеличивая число прямоугольных полосок. Но многоугольник с восемьюстами миллионами сторон все же многоугольник, а не окружность. И восемьсот миллионов рядов стоящих прямоугольников - все еще многоступенчатая лесенка, а не плавная кривая.

Только при беспредельном увеличении числа сторон можно считать, что многоугольник превратится в окружность. Только при беспредельном увеличении числа прямоугольных полосок можно считать, что уничтожены ступеньки. И тогда сумма бесконечно возрастающего числа бесконечно узеньких прямоугольных площадок достигнет своего предела - точного значения площади под кривой.

Математика совершила этот прыжок в бесконечность. Она уловила тот предельный переход, при котором многоугольник становится окружностью, а ступеньки прямоугольников превращаются в плавную кривую. Она нашла предел, к которому стремится сумма при бесконечном возрастании числа слагаемых, каждое из которых стремится к нолю. Этот предел называют интегралом функции.

Интеграл символически обозначают значком ∫, введенным Лейбницем. Он происходит от буквы S-в те времена так обозначали сумму.

О свойствах интегралов, об интегральном исчислении и его применении в различных областях науки и техники написано много монографий, учебников и статей. По нашему короткому рассказу трудно, конечно, представить себе все огромное значение этого понятия в арсенале научных достижений человека. Более того. У многих знакомство с ним может даже вызвать некоторое разочарование. Мы неоднократно упоминали об интегральном исчислении, как об одном из краеугольных камней всей современной математики, а оказывается, все дело сводится к способу вычисления площадей.

Но ведь известно, что существует много других более простых способов вычисления любых площадей с достаточной для практики точностью. Стоит ли для этого прибегать к абстрактному интегральному исчислению, развивать методы интегрирования, создавать сложные машины для их механизации?

Поневоле вспомнишь рассказ А. П. Чехова "Репетитор", где он с тонким юмором описывает, как упорно, но безрезультатно трудились над задачей двенадцатилетний Петя Удодов и его репетитор гимназист семиклассник Зи-беров.

- Это задача, собственно говоря, алгебраическая, - говорит Зиберов, когда у него ничего не выходит с решением.

- Ее с иксом и игреком решить можно...

- И без алгебры решить можно, - говорит Удодов-отец. Он щелкает на счетах, и у него тут же получается ответ.

- Вот-с... по-нашему, по-неученому.

К сожалению, "по-неученому" не всякую задачу решить можно.

Интеграл действительно всегда может рассматриваться как точное значение площади, и ничего больше. Но огромное число математических и практических проблем, связанных с изучением функциональных зависимостей, именно сводится к отысканию формул площадей.

Вспомните о математическом анализе движения самолета, о котором мы рассказывали в начале главы. Там указывалось, что ускорение самолета зависит от действующих на него сил. Они изменяются во времени. Если бы эти силы были постоянны, тогда было бы постоянным и ускорение самолета (или же его и вовсе не было). Каждый мог бы легко вычислить и скорость самолета, летящего с постоянным ускорением. Для этого достаточно умножить ускорение самолета на время движения.

В системе координат постоянное ускорение изображается прямой линией, параллельной горизонтальной оси координат, по которой откладывается время. А скорость - площадь прямоугольника под нею. Эту скорость так же легко найти, как вычислить площадь страницы. Только здесь вместо высоты страницы - ускорение, вместо ширины - время.

Но все дело в том, что силы, действующие на самолет, меняются во времени, а значит, меняется и ускорение. Связь между скоростью, ускорением и силами в этом случае оказывается очень сложной. Она описывается дифференциальным уравнением. Чтобы его решить, приходится искать скорость самолета, имеющего переменное ускорение.

Но когда ускорение переменное во времени - функция времени, - задача усложняется. Ведь теперь нужно вычислять площадь, расположенную под кривой линией, которая показывает, как меняется ускорение. Эта задача такая же сложная, как вычисление площади под кривой линией, которой мы разделили страницу.

Скорость переменного движения можно найти только интегрированием, или, как говорят, интегрированием дифференциального уравнения движения самолета.

Теперь уже нетрудно догадаться, как, зная закон изменения скорости, найти путь самолета. Ведь при равномерном движении путь, равный произведению скорости на время, тоже является площадью прямоугольника. Если же скорость меняется во времени, то путь - площадь под кривой. Чтобы ее вычислить, нужно снова интегрировать, но уже кривую скорости.

Изучение динамических процессов в машинах, электрических цепях, системах автоматического регулирования бывает связано с решением очень сложных дифференциальных уравнений. При этом возникает необходимость многократного повторения операции интегрирования.

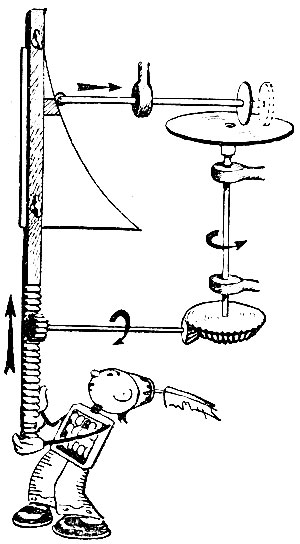
Фрикционный механизм интегрирует

Для механизации процесса интегрирования может служить фрикционная передача. На ее интересные свойства еще в прошлом столетии обратил внимание выдающийся английский физик Уильям Томсон. Он обладал мощным умом и необыкновенной творческой силой. Достаточно сказать, что, написав первую научную работу, когда ему было десять лет, он незадолго до смерти успел закончить 659-ю! Умер он 83 лет.

Среди работ Томсона немало математических исследований. Он был во всех отношениях первоклассным математиком. Умение владеть математическим анализом ученый считал "особой привилегией натуралиста".

На вопрос, что такое математика, Томсон, не задумываясь, написал интеграл

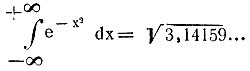
и заметил, указывая на него:

- Математик это тот, для которого справедливость этого равенства столь же очевидна, как дважды два - четыре.

Крупный ученый был незаурядным изобретателем. Ему принадлежало 70 патентов на различные приспособления и приборы. Ему же и принадлежит идея интегрирования с помощью фрикционного механизма - интегратора Томсона.

На рисунке показана схема механического интегрирования кривой, разделяющей нашу страницу. Шаблон, вырезанный по форме этой кривой, укреплен на линейке, снабженной зубчатой рейкой. На него опирается стержень, несущий ролик интегратора. Рейка через систему зубчатых передач вращает диск интегратора.

Вспомните, как фрикционный механизм производил умножение. Здесь, по существу, то же самое: мы интегрируем, а значит, ищем площади маленьких прямоугольничков в виде произведений их оснований на высоты.

Один сомножитель получается просто - это расстояние по горизонтали от рейки до кривой. Чтобы получить другой, надо немного подвинуть шаблон вправо или влево.

Это перемещение и дает второй сомножитель - основание площади, величина которого передается через механизмы на диск интегратора.

Итак, первый сомножитель - высота, второй - основание, а произведение - маленькая площадь, которую, как мы знаем, можно считать площадью прямоугольника. Она-то и фиксируется углом поворота ролика.

Самое замечательное в этом механизме то, что по мере продвижения шаблона вперед угол поворота ролика будет непрерывно увеличиваться в соответствии с площадью, расположенной под пройденным участком кривой. При этом будут складываться ступеньки прямоугольников. Вот таким остроумным путем получают интеграл от функции, которая изображается нашей кривой.

Величину интеграла, то есть площади, можно определять по счетчику, связанному с роликом.

Наш рисунок очень примитивно изображает схему механического интегрирования функции. Современный фрикционный интегратор - это сложный и точный механизм. Его строят в различных конструктивных вариантах.

Если вы посмотрите на интегратор, который входит в состав отечественной, самой мощной в мире машины для решения дифференциальных уравнений, то увидите, как под большим прозрачным колпаком с огромной скоростью, но поразительно плавно вращается стеклянный диск. Он приводится в движение электродвигателем, управляемым дистанционно, с помощью следящей системы.

Долго, без устали можно наблюдать за работой интегратора. Световые блики отражаются от быстро вращающегося диска. Медленно, почти незаметно для глаза передвигается каретка с роликом - второй сомножитель. Неустанно, то быстрее, то медленнее, вращается ролик, увлекаемый трением о диск. Механизм интегрирует - трение решает сложнейшие задачи высшей математики.

Фрикционным интегратором можно интегрировать и функцию, заданную формулами, а не графиком-шаблоном. Но для этого нужны еще специальные устройства. Их называют функциональными.

В предыдущей главе мы познакомились с суммирующим и тангенсным устройствами. Это тоже функциональные устройства. Творцы математических моделей создают самые разнообразные механизмы и электрические системы, моделирующие функции, выраженные формулами.

Интегратор - основное устройство в машине для решения дифференциальных уравнений. Эту машину называют дифференциальным анализа тором.

Впервые анализатор построил знаменитый русский кораблестроитель академик Алексей Николаевич Крылов.

Практические потребности опытового бассейна, которым руководил ученый, побудили его искать способы ускорения вычислений. Знакомство с научными работами о вычислениях и изучение трудов Томсона привели Крылова еще в 1887 году к мысли о создании машины, пригодной для интегрирования дифференциальных уравнений. Уже в 1904 году ученый разработал ее теорию.

Несмотря на то, что постройка машины совпала с войной 1905 года и велась с большими перерывами, он реализовал свою идею. Через семь лет под руководством Крылова один из искусных петербургских механиков построил первый дифференциальный анализатор. Машина была вполне законченным устройством со многими оригинальными механизмами, предназначенными для изучения вибраций корабля. Но послужила она недолго и во время эвакуационной суматохи в начале первой мировой войны бесследно пропала. Восстановить же потом дифференциальный анализатор не удалось.

В последующие годы несколько механических дифференциальных анализаторов было построено в США и в Европе. В 1937 году под руководством члена-корреспондента Академии наук СССР И. С. Брука дифференциальный анализатор был создан в Советском Союзе. Много лет на нем с успехом решались самые разнообразные математические задачи.

Вскоре после Великой Отечественной войны советские инженеры и конструкторы приступили к созданию самой большой в мире электромеханической машины для решения дифференциальных уравнений. Многолетний упорный творческий труд завершился блестящим успехом. Мощный дифференциальный анализатор был построен и поступил в нормальную эксплуатацию. Его назвали "Интегралом".

В этой огромной математической модели, занимающей около 250 квадратных метров, имеется двадцать четыре очень точных фрикционных интегратора. Они работают совместно с функциональными, множительными, суммирующими и другими устройствами.

Сотни электродвигателей, следящих систем и усилителей, тысячи реле управляют работой машины, и много километров проводов связывают устройства друг с другом. Настройка машины, контроль и решение задач происходят автоматически.

"Интеграл" - уникальная и очень дорогая машина. Она стоит много миллионов рублей.

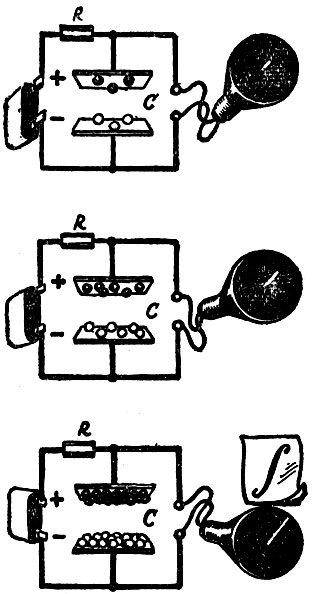
Конденсатор накапливает заряды - электрическая цепь интегрирует

Потребность в математических моделях для интегрирования дифференциальных уравнений очень велика. В них нуждаются и научные организации и конструкторские бюро.

Ученым и инженерам повседневно приходится решать дифференциальные уравнения, интегрировать сложные зависимости. Чтобы сократить сроки проектирования новых инженерных сооружений, создания новых машин и автоматов, быстрее проникнуть в закономерности физического процесса, нужно всегда иметь под рукой готовый к работе, дифференциальный анализатор.

Нужны недорогие, малогабаритные и быстродействующие машины массового применения. Такими являются электронные модели для интегрирования дифференциальных уравнений.

Так как основой электронной модели является электрический интегратор, то познакомимся с ним подробнее. Вам не придется следить за нашим рассказом по сложной электрической схеме, окунуться в паутину проводов и разнообразных электрических деталей.

Электрическая интегрирующая цепь представляет собой соединение обычного конденсатора и сопротивления. Интегрируемая функция в виде напряжения подается на вход схемы. Снимаемое же на выходе напряжение - это уже найденный интеграл. Непосредственно интегрирующим элементом является емкость, то есть обыкновенный конденсатор. Он накапливает заряды.

Счетчик такси интегрирует ско- рость расхода денег пассажира

Накопление - основа интегрирования. Вы едете в такси. Перед вами счетчик. Он указывает пройденный путь. Но для вас, пассажира, этот путь указывается в масштабе стоимости одного километра пробега. Счетчик, накапливая количество пройденных километров, тем самым интегрирует по времени скорость движения автомобиля. Или, если хотите, он интегрирует скорость расхода ваших денег.

Чтобы резко улучшить процесс интегрирования - повысить точность, - емкость включают в цепь электронного усилителя.

Электронный дифференциальный анализатор состоит обычно из шести или двенадцати таких интегрирующих усилителей. Кроме того, как и в механическом анализаторе, в нем имеются суммирующие, множительные и функциональные устройства. Но все переменные, входящие в дифференциальные уравнения, здесь моделируются не механическими перемещениями, а электрическими напряжениями.

Как же электронная модель интегрирует дифференциальные уравнения?

Представьте себе массу, подвешенную на пружине. На нее действует постоянная сила земного тяготения. Чтобы найти закон, по которому в зависимости от времени меняется расстояние от массы до опоры, нужно составить дифференциальное уравнение движения массы. Оно вытекает из второго закона Ньютона, которым мы уже пользовались при анализе движения самолета.

В нашем примере и ускорение, и скорость массы, и ее расстояние до опоры меняются в зависимости от времени. А мы уже знаем, что это значит. Все они - функции времени.

Нам также известно, что скорость есть интеграл от ускорения, а путь - интеграл от скорости. Поэтому, интегрируя ускорение, найдем скорость, а интегрируя скорость, найдем расстояние от центра массы до точки опоры.

Для решения этой задачи на электронной модели имеется два интегратора. На вход первого подается напряжение, пропорциональное ускорению. После интегрирования на выходе возникает напряжение, уже пропорциональное скорости. Оно поступает на вход следующего интегратора и снова интегрируется. Напряжение на выходе второго интегратора и будет меняться пропорционально расстоянию массы от опоры.

А откуда взялось напряжение, пропорциональное ускорению, которое мы подали на вход первого интегратора? Его вырабатывает суммирующая электрическая схема. Как она действует, мы знаем. На ее входы подаются напряжения, пропорциональные силам, приложенным к массе и вызывающим ускорение. В нашем примере их две: одна - постоянная, которую мы приложили к массе, другая - переменная сила упругости пружины. Она зависит от растяжения пружины, то есть положения массы. Поэтому напряжение со второго интегратора, определяющее эту силу, и подается на вход суммирующей цепочки.

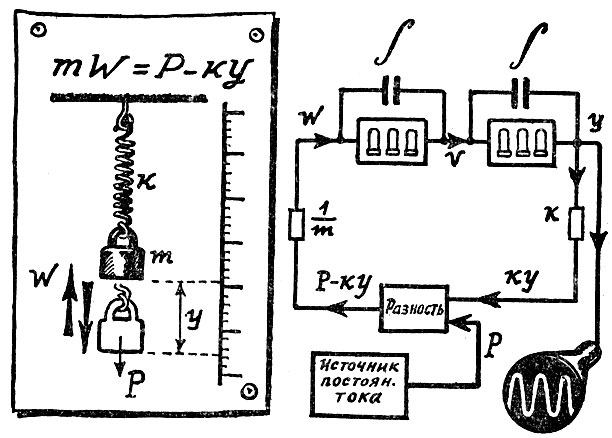
На экране осциллографа - график движения массы в зависимости от времени. Он получен электронной моделью

Постоянное напряжение, пропорциональное постоянной силе, подается на второй вход суммирующей схемы.

Чтобы получить готовое решение, выходное напряжение со второго интегратора подается на трубку электронного осциллографа. И на матово-белом экране тотчас же появляется светящаяся кривая линия. Это график движения массы в зависимости от времени.

А теперь вспомните: "...Группа людей с напряженным вниманием смотрит на экран электронного осциллографа. На матово-белой поверхности медленно проплывает светящаяся точка. Она оставляет за собой след - тонкую изумрудного цвета змейку причудливой формы". Это разгадка сложного движения самолета.

Авторы долго раздумывали, как закончить рассказ о "математическом зеркале".

Можно было бы описать советские математические модели. Но их очень много. Чтобы лишь бегло познакомить со всеми моделями, нужно немало времени.

Можно было бы рассказать об использовании моделей для решения практических задач. Но и об этом пришлось бы писать очень много. Область применения моделей неисчерпаема, как неисчерпаемо разнообразие явлений в окружающем нас мире.

Поэтому в заключение мы лишь обратим внимание на то, как многообразны различные процессы, лежащие в основе моделирования.

Посудите сами: механические, гидравлические, электрические, акустические - любой из известных нам физических процессов может найти место в моделировании.

Без четкого понимания принципов математического моделирования и его возможностей трудно ориентироваться в современной вычислительной технике, оценивать ее достижения и перспективы. Вот почему нам пришлось задержать внимание читателя и преподнести, быть может, скучноватый, но полезный рассказ о работе моделирующих устройств.