б) Информации

Теория информации стремится количественно выразить физическое содержание переданного сообщения как меру определенности в переданном сообщении, то есть информации¹. Впервые к этому прибег Кюпфмюллер в 1924 году, выразивший это содержание следующим образом:

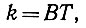
где Т означает продолжительность сообщения, преобразованного в сигналы, a В - потребную ширину полосы частот сигналов, то есть диапазон от самой низкой до самой высокой из использованных частот при передаче сообщения по каналу. Величины Т и В обратно пропорциональны, то есть при большей продолжительности передачи может сузиться полоса частот и наоборот, причем без изменения количества информации.

¹ (Слово "информация" здесь используется также и в качественном смысле как синоним слова "сообщение".)

В 1928 году Хартли ввел третий размер, то есть амплитуду¹. Согласно Хартли, для передачи сообщения и для структуры сигнала важное значение имеет различие в амплитуде, повышающее разнообразие, различимость канала передачи. Информация, по Хартли, выражается следующим образом:

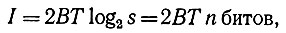
¹ (См. R. V. Har11eу, Transmission of Information, "Bell. Syst. Tech. Journal", Vol. 7, 3, p. 535. (Русск. перев.: Р. Хартли, Передача информации, сб. "Теория информации и ее приложения", М., ,1959.))

где В - ширина полосы частот, Т - длительность передачи сообщения, a s - число поддающихся различению ступеней амплитуды, двоичный логарифм которого равен n битов, двоичных единиц информации¹. Ширину полосы частот Хартли выражает следующим образом:

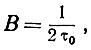
¹ (Слово "бит" является сокращением английских слов "binary digit" и означает элементарную единицу информации (1 бит = log22), равную двоичному логарифму двух, то есть логарифму с основанием 2. Количество информации зависит от выбора сообщения и измеряется логарифмом числа необходимых при этом выборов. Например, log216=4 бита означает, что информация характеризуется четырьмя битами и что число выборов равно 16. Двоичная азбука удобна для передачи сообщений благодаря ее простоте и точности, она исходит из элементарного выбора между положительным и отрицательным решением или ответом я имеет только два символа: 1 и 0. Согласно Джону Лоэбу, бинарный код встречается впервые у английского математика Доджсона, написавшего под псевдонимом Л. Кэррол известную книгу "Алиса в стране чудес". Героиня книги Алиса, которая не может договориться с кошечкой, высказывается в одном месте, что если бы кошка отвечала на вопросы утвердительно путем мяуканья, а отрицательно путем мурлыканья, то с ней можно было бы говорить обо всем.)

где τ₀ - продолжительность одного двоичного шага. Информационное содержание сообщения можно выразить с помощью трех координат: 2В, Т и n.

В 1949 году Шеннон¹ усовершенствовал формулу информации. В то время как Хартли считал выбор сообщения из множества проблемой в основном психологической, Шеннон считает эту проблему чисто статистической. Количеством информации он считает энтропию, являющуюся мерой неопределенности в каком-то сообщении, которая после приема сообщения устраняется в той или иной степени, так что она выражает и меру полученной информации. Эта энтропия соответствует больцмановскому выражению термодинамической энтропии, и ее можно математически выразить с помощью теории вероятности следующим образом.

¹ (См. С. Shannon, The mathematical Theory of Communication, Urbana, 1949. (Русск. перев.: К- Шеннон, Математическая теория связи, "Работы по теории информации и кибернетике", Издательство иностранной литературы, 1959.))

Система случаев А₁, А₂, ..., А_n полна, если всегда наступает именно один из этих случаев. Их вероятность можно обозначить в виде р₁, р₂, ..., р_n. Сумма этих вероятностей равна единице. Так называемая конечная схема получается тогда, когда дана полная система случаев и их соответствующие вероятности. Эта схема описывает какое-то состояние неопределенности. Общая формула конечной схемы такова:

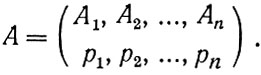
Таким образом, например, конечная схема при бросании шестигранной кости такова:

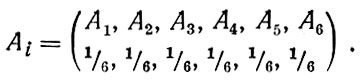
Конечная схема имеет некоторую неопределенность, то есть мы не знаем, какой из случаев наступит (на какую грань кость падет). В качестве меры неопределенности конечной схемы может служить энтропия, обозначенная как Н. Формула этой энтропии, по Шеннону, такова:

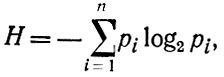
где определяем в соответствии с непрерывностью функции xlog₂x : 0 log₂0 = 0

Таким образом, для конечной схемы бросания кости получаем:

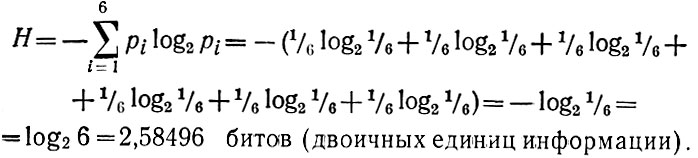
Если какое-то р_i =1, то остальные равны нулю, и H также равна нулю, так как log₂p = 0 для р=1 или p=0. Энтропия в этом случае, следовательно, минимальна. Наоборот, энтропия максимальна при равенстве всех вероятностей р₁, р₂, ..., р_n между собой. Между нулевой и максимальной мерой неопределенности имеется бесконечное число средних возможностей, когда H лежит между 0 и log₂n:

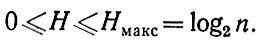
Если H мала, то это значит, что между системой случаев имеется один случай или небольшое число случаев, вероятность появления которых значительно превышает вероятность появления других случаев. Энтропию обозначают как меру неопределенности, информацию же, наоборот, как меру определенности. Если убывает энтропия, возрастает информация и наоборот. Если начальная неопределенность перед бросанием кости равна log₂6, то эта неопределенность устранена выполнением броска таким образом, что выпадет одна грань кости и неопределенность будет тогда равна log₂l, то есть будет нулевой. Информацию мы получаем путем устранения неопределенности. Конечно, не обязательно должна идти речь о полном устранении, особенно если гут действует шум.

При конкретном использовании канала некоторые возможные состояния вообще не встретятся, другие встретятся лишь редко, третьи же встретятся часто. Поэтому можно обойтись каналом и с меньшим объемом. Если, например, все сообщения одинаковы, они заранее известны или о них можно судить по прежним, ранее принятым сообщениям, то источник не будет передавать ничего нового, количество передаваемой информации будет низким. Случайный характер описываемого события приводит к случайному выбору сообщения из многих возможных, и мера информации, поэтому описывается при помощи методов теории вероятностей. Мы указали, что конечная схема состоит из полной системы случаев и соответствующих им вероятностей. При передаче сообщений производится выбор одного из элементов конечной схемы в соответствии с распределением вероятностей. Каждая конечная схема представляет какую-то неопределенность выбора своих элементов, и эта неопределенность исчезает после выполнения выбора. Максимальная неопределенность имеет место при равномерном распределении вероятностей, а, следовательно, и получение информации в таком случае наибольшее, так как это соответствует устранению большой неопределенности. Схема

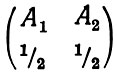
имеет, следовательно, большую неопределенность, чем схема

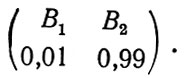
Степень неопределенности возрастает с большей равномерностью распределения вероятностей и с ростом числа элементов схемы. Мера неопределенности выбора в схеме является и мерой количества информации для одного выбора, так как выбор нарушает неопределенность. Эта мера является функцией всех вероятностей, и она изменяется плавно при плавном изменении вероятностей. Единицей измерения количества информации или энтропии является единичный выбор из двух одинаковых вероятных возможностей.

Энтропия является, по Шеннону, мерой свободы выбора, априорной неопределенности. Таким образом, энтропия характеризует не то, что передано, а то, что могло бы быть передано. Выбор сообщения производится источником сообщения на входной стороне канала, чем характеризуется энтропия источника сообщений. Эта энтропия измеряется либо в символах (на один выбор), либо в единицах времени (секундах). Энтропией 32 символов является 5 двоичных единиц информации (битов), 16 символов - 4 единицы, то есть в общем виде

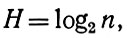
где n - число символов.

Приведенная Шенноном формула энтропии относится к сообщениям, выраженным в дискретных величинах. Наряду с этим существует и непрерывная информация. Непрерывный процесс передачи сообщений можно считать крайним случаем дискретного процесса, если континуум сообщений и сигналов разделится на большое число дискретных частей. Можно непрерывные величины квантовать с определенной степенью приближения в дискретных величинах. Далее можно было бы сказать, что для непрерывного алфавита число возможных сообщений, собственно говоря, бесконечно, оно поддается вычислению путем преобразования этого алфавита в дискретный. Непрерывный источник передает сообщения в виде волн. Количество информации здесь задано числом инструкций "да - нет", необходимых для выбора волновых видов сообщения из данного комплекса. Алфавит непрерывного источника дан, например, различением уровней амплитуды. При передаче сообщения речь идет о выборе из состояний источника волн.

Сигнал, выходящий из источника, является временной серией двоичных решений. Таким образом, волну можно квантовать в двоичном коде.

Энтропия непрерывного распределения задается, по Шеннону, формулой

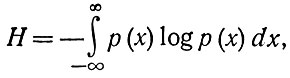
где р (х) - -плотность вероятностей. При двух аргументах к и у энтропия задается как

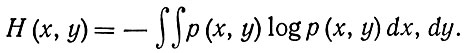
При n - размерном распределении p(x₁,...,x_n) энтропия равна

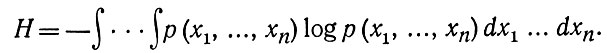
Вход в непрерывном канале является постоянной функцией времени f (t), выход задан искажением этой функции. Количество переданной информации задано как и в дискретном канале разностью энтропии входа и выхода¹.

¹ (Энтропия входа, то есть энтропия источника, показывает информационное содержание переданных символов. Энтропия выхода показывает информационное содержание принятых символов. Далее в теории информации говорится об объединенной энтропии, то есть об объединенной энтропии переданных и принятых символов. Диссипация означает условную энтропию выхода, если известны вероятности входа. Эквивокация - это условная энтропия входа, если известны вероятности выхода.)

Непрерывные сигналы, несущие сообщения, можно по-разному модулировать. Модуляция является изменением во времени одного из параметров физического процесса, несущего информацию. Сигнал должен иметь возможность принимать различные состояния. На текущей субстанции, движущейся от передатчика к приемнику, передатчик может посредством модуляции делать пометки, представляющие выбор различных символов какого-то алфавита. Можно модулировать световые или звуковые волны. Примером модуляции в частоте является игра на скрипке или человеческая речь. Наряду с этим можно выполнять модуляцию и в амплитуде или в фазе. Средством передачи информации служат основные или несущие колебания, на которых производится модуляция. На одном несущем основании можно передавать одновременно много сообщений, которые на выходе подразделяются как различные модуляционные функции. Примером модуляции может служит речь, изменение электрического тока в проводе, нервное возбуждение и т. д.