в) Отображение сообщения

Теория информации занимается не конкретным содержанием сообщения, а только его физическим содержанием, которое можно выразить количественно. Согласно Шеннону, семантические аспекты коммуникации независимы от технических аспектов. Технический аспект будто бы обходится без семантического аспекта, но не наоборот, семантический аспект не может быть без технического аспекта, то есть определение смысла сообщения зависит от передачи его. Таким образом, в подходе Шеннона теория информации абстрагируется от семантического содержания сообщения.

Однако вопрос о связи семантического и технического аспектов в теории информации все еще является предметом постоянных дискуссий. На важность семантического аспекта указывали, в частности, Мак-Кэй, Карнап, Бар-Хиллел и другие¹. С точки зрения технической теории коммуникаций информация не обязательно должна быть связана с понятием смысла и конкретного содержания сообщения. Следовательно, это означает, что с точки зрения меры информации два сообщения могут быть математически эквивалентны, даже если одно из них будет бессмысленным. Телеграфистка, например, может быть при исполнении своих обязанностей равнодушной к конкретному содержанию передаваемого сообщения. Ей может быть все равно, радостно или печально это содержание. Ее интересует лишь длина сообщения, количество букв и слов, а может быть, и их вероятностная зависимость влияющая на скорость кодирования.

¹ (См. D. M. MасКау, Quantal Aspects of Scientific Information, "Phil. Mag.", 1950, p. 289; The Place of "Meaning" in the Theory of Information, в: С. Cherry (ed.), "Information Theory", London, 1956; J. Bar-Hill el, R. Сarnap, Semantic Information, в: W. Jackson (ed.), "Communication Theory", London, 1953.)

С философской точки зрения технический, количественный и семантический, качественный аспекты не независимы друг oт друга. Нет независимости (друг от друга) так называемой селективной и семантической информации, технического и семантического шума. Однако саму по себе теорию информации не обязательно должно интересовать конкретное содержание сообщения, эта теория рассматривает преимущественно его математическую сторону, и сообщение означает для нее лишь определенное -количество различающихся друг от друга состояний. Способность к передаче и изображению сообщения означает способность разложить сообщение на определенное число разнообразных состояний. Каждое событие, о котором подается сообщение, может находиться в каждый момент в одном из многочисленных возможных состояний. Вход события означает изменение этих выбранных состояний. События отличаются друг от друга числом возможных состояний и особенностями выбора. Количество возможных состояний может быть изображено сообщением в дискретном или в непрерывном виде. Каждому событию соответствует состояние физического процесса, представляющего определенный сигнал или совокупность сигналов сообщения.

Сообщение можно изобразить на сетке координат. Если мы временно отвлечемся от частоты сигналов, то можно нанести на одну координату квантованные ступени амплитуды, а на другую - время. Сообщение определенной длины, определенной продолжительности зависит от выбора из данного алфавита. Следовательно, оно зависит от временной последовательности, указывающей длину сообщения n, и от выбора из т ступеней при каждом значении n. Совокупность возможных сообщений V равна тⁿ (т - число букв алфавита, n - число букв сообщения). Если, например, т = 4 (А, В, С, D), а n=1, то V=4. Если т=4, n=2, то V=16 (AB, AC, AD, АА, ВВ, ВА, ВС, BD, СС, СА, СВ, CD, DD, DA, DB, DC). Совокупность возможных сообщений - это запас, из которого выбираются определенные конкретные сообщения. Информационное содержание сообщения равняется двоичному логарифму из этого запаса:

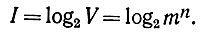
Этот логарифм показывает число двоичных единиц информации, двоичных решений, которые необходимо выполнить при передаче сообщения и которым, следовательно, задается информационное содержание сообщения. Квант информации, так называемый элемент, атом сообщения или логон, задается одной двоичной единицей информации, одним решающим шагом. Таким образом, можно изобразить сообщение на растре символов, где запас сообщений задан n рядами из т точек, и он выражает число V различных информационных кривых на растре, равное тⁿ. Если, например, мы имеем алфавит с пятью буквами А, В, С, D, E, то мы можем изобразить на растре сообщение BEDA длиной в четыре буквы следующим образом:

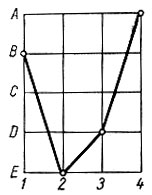
Pис. 3 Отображение сообщения на растре символов

Тонкость растра определяет отличительность в сообщении. Эта тонкость может быть обусловлена, например, зернистостью фотографической бумаги, степенью свечения телевизионного кинескопа и т. п. На этом растре можно изобразить сообщение в виде определенной выбранной кривой, и информацию в этом сообщении мы будем измерять по количеству двоичных единиц информации, которым эта кривая задана на растре. Если, например, т=10, а n=5, то V=10⁵, a I=log₂10⁵ = 51og₂10, что равно 5·3,32193 битов = 16,60965 битов.

Некоторые ученые, работающие в области теории информации, например Мак-Кэй, Габор и др., стремятся анализировать так называемую информационную ячейку, то есть логон. Согласно Мейер-Эпплеру¹, двухразмерное матричное изображение этих ячеек выглядит таким образом:

¹ (W. Mеуег - Eppler Informationstheorie, "Naturwiss.", H. 15, 1952, S. 341.)

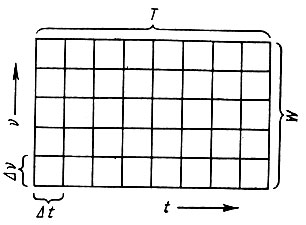
Pис. 4. Двухразмерное изображение информационных ячеек (по Мейер-Эпплеру)

W - здесь ширина полосы частот, Т - продолжительность передачи, a t - частотный и временной диапазон информационной ячейки, то есть логона. Если ввести третью координату - энергию, то получим так называемую информационную призму:

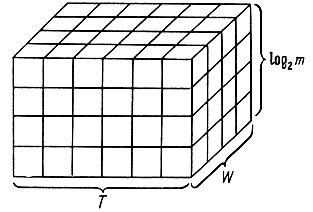
Рис. 5. Информационная призма (по Мейер-Эпплеру)

Третий размер задан как 2log₂m, где m - число так называемых метронов, то есть различных энергетических ступеней (поддающихся различению ступеней амплитуды). Процесс, ограниченный W, T и т, полностью задается числом M информационных единиц и выражает меру потребного "нагрузочного" пространства определенного передаваемого сообщения:

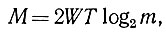
что соответствует формуле информации Хартли.

Согласно Дж. Лоэбу¹, логон является последним элементом, наименьшим поддающимся различению сигналом, зерном амплитуды. Чтобы возможно было различать дифференциацию амплитуд, амплитуда сигнала не должна быть ниже амплитуды помех; крайний случай имеет место тогда, когда обе эти амплитуды равны; да нужно выбрать между двумя возможностями: 1) сигнал существует, 2) сигнал не существует, что и является крайним пределом отличительности, характеризующим логон. Лоэб обращает внимание на зависимость определения атома сигнала и гейзенберговского соотношения неопределенностей.

¹ (J. Loeb, La cybernetique, "La Technique Moderne", vol. 44, 1952, p. 193.)

Распределение сообщения по ячейкам и его геометрическое изображение дает возможность исследовать так называемое пространство сообщений. Сообщение, выбранное на входе и переданное по каналу, изображено в информационном пространстве выхода. Эта передача зависит от пропускной способности канала. Эта пропускная способность в свою очередь задается пространством передачи, и ее можно определять с помощью информационных ячеек.