4. Вероятность и разнообразие

Если мы имеем какое-то множество элементарных символов, то есть алфавит, то при передаче сообщений мы производим последовательные выборы из этого множества. Наши выборы управляются вероятностно, причем их вероятности могут зависеть от предшествующих выборов. Так, например, в речи мала вероятность того, что после слова "поскольку" будут следовать слова "так как". Таким образом, некоторые группировки слов или букв являются неправдоподобными, невероятными; вероятность некоторых группировок слов или букв мала или даже нулевая, так как такие группировки бессмысленны. Последовательность символов, связанных с определенными вероятностями, - это стохастический процесс, и его особый случай, когда вероятность появления определенного символа зависит от вероятности появления одного предшествующего символа, - это так называемая марковская цепь или стохастический марковский процесс. Следовательно, вероятность определенного выбора может зависеть от предшествующих выборов.

Символы, из которых состоит сообщение, не обязательно должны иметь одинаковую вероятность, они могут иметь различную относительную частоту появления. Чем реже данный символ появляется, тем больше информации он с собой несет, тем большую степень неожиданности он имеет. Неодинаковые вероятности появления символов можно также изобразить с помощью двоичных выборов, то есть для нахождения каждого символа алфавита требуется определенное число последовательных двоичных делений этого алфавита. Среднее ожидаемое количество информации измеряется в двоичных единицах информации на символ по формуле

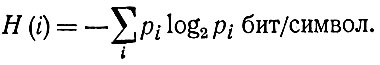
Вероятность определенной последовательности знаков равна произведению вероятностей всех этих знаков, если все эти вероятности независимы друг от друга.

Частота появления знаков может быть независима от появления других знаков. Энтропия для независимых знаков аддитивна по формуле

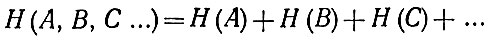
Принятый сигнал может быть вероятностно связан с переданным сигналом, и из него можно получить информацию об этом переданном сигнале. Функция р (х/у) выражает вероятность того, что было передано х, если было принято у, что и является так называемой вероятностью апостериорной в отличие от априорной вероятности р (х) высланного сигнала.

Вопрос о вероятностной зависимости очень важен для передачи сообщений. При передаче сообщения происходит отображение элементов поддающегося измерению пространства сообщений источника элементами поддающегося измерению пространства сообщений получателя, что совершается вероятностно, так как при этой передаче проявляют свое действие помехи и принятое сообщение имеет меньшее количество информации, чем переданное. Согласно Перезу¹, априорное распределение вероятности в пространстве сообщений источника можно рассматривать как микроскопическое состояние, изображенное каким-то макроскопическим состоянием в поддающемся измерению пространстве получателя, которое (макроскопическое состояние) здесь задано другим, апостериорным распределением вероятности, другой, меньшей отличительностью на стороне выхода, чем на стороне входа.

¹ (См. A. Perez, Matematicka teorie informace, "Aplikace mate-matiky", № 1 - 2, 1958.)

Разнообразие переданного сообщения всегда больше или в крайнем случае одинаково с разнообразием принятого сообщения. Таким образом, при передаче сообщения происходит редукция, ограничение разнообразия. Разнообразие принятого сообщения может быть больше разнообразия переданного сообщения в случае, когда шум вносит новые элементы в переданное сообщение. Однако это не повышает отличительности принятого сообщения, для которого решающее значение имеет точное воспроизведение входа: например, вместо переданного OKY можно принять OKYF или OLVF.

Вопросом о разнообразии сообщений и его ограничении занимался Шеннон¹, согласно которому в дискретном канале без помех производится при передаче информации последовательность выборов из конечного множества элементарных символов S₁...S_n. Каждый из символов S_i имеет определенную длительность во времени (например, в азбуке Морзе точка длится одну единицу времени, тире - три единицы времени, промежуток между символами - три единицы времени, а промежуток между словами - шесть единиц времени). Разнообразие возможных последовательностей символов больше разнообразия действительно переданных последовательностей, то есть в качестве сигналов для передачи через канал допустимы лишь определенные последовательности; следовательно, при выборе всегда совершается определенное ограничение разнообразия. При приеме происходит дальнейшая редукция этого разнообразия.

¹ (См. С. Shannon, The Mathematical Theory of Communication.)

Шеннон подчеркивает, что последовательности символов при передаче сообщений не совершенно случайны, а имеют определенную статистическую структуру. Так, например, в английском языке буква E чаще встречается, чем О, а последовательность ТН чаще встречается, чем последовательность ХР и т. п. Эта статистическая структура дает возможность экономить время, а этим и пропускную способность канала при кодировании последовательностей символов в сигналы. Поэтому в телеграфии используют для буквы E короткий код - точку, тогда как, например, для редко встречающихся букв О, X и Z применяют более длительные коды элементарных символов. Эти свойства сообщений, то есть статистической структуры последовательностей, используются в так называемых коммерческих кодах, где определенные, чаще встречающиеся, слова и даже фразы кодируются с помощью четырех или пяти буквенных кодов групп. Сокращенный код применяется также для стандартизированных телеграмм.

Выбор последовательности символов, согласно определенной вероятностной зависимости, - это стохастический процесс. Шеннон приводит пример нескольких различных ступеней выбора букв. Эти буквы можно использовать так, что их вероятности будут независимы друг от друга. Более сложный выбор имеет место тогда, когда при выборе символов мы имеем дело с зависимыми вероятностями, то есть, например, когда имеется зависимость от одной предыдущей буквы. Статистическую структуру выбора можно описать множеством переходных вероятностей p_i(j), что означает вероятность того, что после буквы i следует буква j. Так называемая диграммная вероятность выражает относительную частоту появления диграмма (двухбуквенного соединения) ij. Вероятность появления буквы i, то есть буквенную частоту мы обозначаем как p (i), переходную вероятность - как р_i (j), а диграммиую вероятность- как p (i,j). Триграмм выражает зависимость проявления данной буквы от двух предыдущих букв, и эту зависимость обозначают как p (i, о, k) или p_ij (k). В общем виде n - грамм обозначают, как

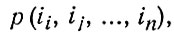
а переходную вероятность - как

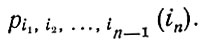
Таким стохастическим процессом является текст, состоящий из последовательности букв или последовательности слов. Шеннон указывает, что с помощью переходных вероятностей можно создать искусственный язык и что серией искусственных языков можно приблизиться к вероятностной структуре естественного языка. В своем примере Шеннон использует буквы и слова с определенными вероятностями. На первой ступени приближения производится выбор букв, имеющих одну и ту же и независимую друг от друга вероятность:

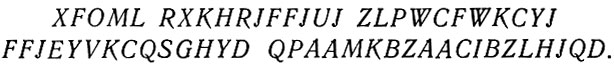
На второй ступени выбор производится так же независимо, но буквы имеют такую частоту появления, как в английском тексте:

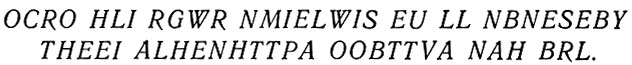
На третьей ступени приближения используются ди-граммные структуры, то есть выбор буквы здесь всегда производится с вероятностью, зависящей от частоты появления предшествующей буквы, то есть, например, в общем виде после i следует с максимальной вероятностью буква j:

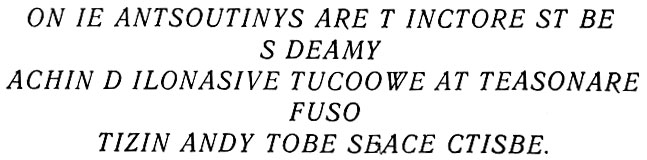
На четвертой ступени приближения используются три-граммные структуры английского языка, то есть здесь буквы выбраны с вероятностью, зависящей от двух предшествующих букв:

На пятой ступени приближения не используются какие-либо граммы, а совершается переход к словам. Слова здесь выбраны независимо друг от друга, но с учетом соответствующей частоты их появления:

И наконец, на шестой ступени приближения используются переходные вероятности слов, но без учета дальнейшей более сложной структуры (грамматической, синтаксической и т. д.):

Подобные примеры искусственных языков, построенных на вероятностных зависимостях, приводят для немецкого языка Мейер-Эпплер и Кюпфмюллер ¹. Мейер-Эпплер приводит последовательности букв по марковским цепям от нулевого до третьего ряда (первый ряд - это диграммы):

¹ (W. Meyer-Eppler, Grundlagen und Anwendungen der Informationstheorie, Berlin, 1959; K. Küpfmü11er, Die Entropie der deutschen Sprach, "Fernmeldetech. Zschrift", № 7, S. 265.)

Далее Мейер-Эпплер приводит марковскую цепь первого ряда из последовательностей немецких слов:

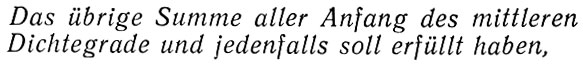
что напоминает дадаистскую¹ конструкцию; смысл имеют здесь лишь пары слов.

¹ (Дадаизм - западноевропейское реакционное течение в литературе и изобразительном искусстве. В литературе дадаисты стремились к изгнанию смысла и логики, предлагая бессмысленный набор слов. - Прим. ред.)

Кюпфмюллер приводит последовательности немецких букв, аналогично тому, как это делает Шеннон. Нулевой ряд представляет совершенно случайные последовательности букв. Первый ряд - последовательности, соответствующие вероятностным частотам букв в немецком языке. Второй ряд - диграммные зависимости. Третий ряд - триграммные зависимости, четвертый ряд - зависимости группы из четырех букв (выбор букв совершается здесь с вероятностью, зависящей от частоты появления трех предыдущих букв):

Вероятностная структура речи определяет надежность, зависимость определенных последовательностей букв и слов. Искусственный язык первой ступени имеет большую свободу выбора, и поэтому он несет с собой немного семантической информации. Произвольность выбора здесь связана с высокой степенью избыточности в языке. Наоборот, чем ниже избыточность, тем больше сжатие семантического содержания. Например, в кроссворде твердо закреплена последовательность букв и не допускается никакая свобода, значит, здесь избыточность нулевая. Свобода выбора слов для кроссворда связана со степенью избыточности данного языка. При решении кроссворда выбор соответствующих слов тем более труден, чем больше избыточность данного языка; на языке с большой избыточностью всегда приходят на ум много кажущихся возможными слов для данного искомого слова. Поэтому более сложные кроссворды можно составлять лишь на языках с низкой степенью избыточности. Например, трехразмерный кроссворд можно было бы создать только для языка с избыточностью в 33%.

Модели искусственных языков Шеннона имеют специальное значение не только для техники связи. Рост когерентности и изменение вероятностной зависимости характерны и для развития познания, так что можно говорить о росте семантической информации, о росте смысла. Как показал еще Шеннон, можно было бы продолжать заниматься построением высших ступеней выбора, если ввести в это построение учет вероятностей сложных грамматических, синтаксических и т. д. структур. Это было бы, конечно, очень трудно и требовало бы тщательного математического анализа языковых синтаксисов и других сложных языковых зависимостей.

Следующей стадией построения высших ступеней выборов был бы учет не только степеней приближения искусственных языков к какому-то естественному языку, но и последовательное приближение к совершенной системе отображения объективной реальности. Тогда мы бы, следовательно, считали объективную реальность сложным контекстом зависимостей и закономерностей, к которому мы приближались бы какими-то более упрощенными контекстами (иначе говоря, если бы мы стали отображать разнообразие объективной реальности каким-то редуцированным разнообразием, но вероятностно зависящим от первого). Весь этот вопрос связан и с теорией предсказания. Рост количества информации по мере развития познания дает возможность роста предсказания, а этим и снижения избыточности в познании. Трудность состоит здесь, конечно, в том, что в то время как в моделях Шеннона известно то, к чему мы стремимся приблизиться - естественный язык, в вопросе познания и семантической информации то, к чему мы стремимся приблизиться, мы знаем лишь приближенно.

При передаче сообщений большое значение имеет случайность, поскольку помехи искажают сигнал, так что на выходе мы получаем лишь некоторое вероятностно определенное сообщение. Следовательно, мы ищем определенную правильность в какой-то неправильности, и в этом, собственно говоря, и состоит существо познания: изыскивание упорядоченности в неупорядоченном. Ограниченность познания обусловлена невозможностью иметь в нашем распоряжении огромную, собственно говоря, бесконечную массу данных об изучаемом объекте и необходимостью выбирать из этого сложного разнообразия какие-то существенные зависимости. Следовательно, мы совершаем определенную редукцию этого разнообразия; с помощью упрощений и абстракции мы постигаем общее и существенное. Без этого невозможна была бы никакая наука. Так, например, физика газов не может опираться на информацию о каждой молекуле газа, она вынуждена ограничиваться абстракцией и только статистическим определением.

С полной случайностью и неправильностью мы встречаемся в теории информации при рассмотрении вопроса о так называемом белом шуме. Этот белый шум изображен совершенно неправильной кривой, в спектре которой не выделяется какая-либо частота и где имеется равномерное распределение амплитуд. Полная правильность не несет с собой, собственно говоря, никакой информации, потому что здесь теряется упомянутый выше момент неожиданности. Противоположностью правильности является именно полная неправильность и случайность, представляемая белым шумом. В сообщении, закодированном в виде белого шума, была бы, следовательно, скрыта максимальная мера информации; с другой стороны, хотя это на первый взгляд кажется парадоксальным, для такого кодированного сообщения требовалось бы лишь минимальное пространство передачи. Однако при передаче информации мы имеем всегда дело со смесью правильности и неправильности, с сочетанием моментов предсказания и неожиданности.

В объективной реальности как источнике сообщений скрыто для познающего субъекта максимальное количество информации, но субъект не может воспринять всю ее, так как его пропускная способность сильно ограничена. Субъект воспринимает, принимает, истолковывает и познает лишь кое-что из огромной сложности разнообразия объективной реальности: возможность познания и состоит в редукции этого разнообразия. Эта максимальная информация настолько сложна для субъекта, что она представляется ему хаосом, максимальными неправильностью и неопределенностью, из которых он выбирает лишь определенные сообщения и выводит из них некоторую определенность. Говоря словами поэта, объективная реальность представляется для субъекта "очами хаоса, светящимися сквозь вуаль порядка". Редукция разнообразия, совершаемая субъектом, означает раздвоение на определенное и неопределенное, определимое и неопределимое, информацию и энтропию. Однако по мере развития познания растет удельный вес информации и убывает удельный вес энтропии в познании, то есть изменяется распределение вероятностей в разнообразии картины мира.