3. Избыточность

Максимальная энтропия алфавита достигается при равенстве вероятностей всех символов, что представляет собой наиболее экономичный оптимальный код, который, однако, при реальной передаче трудно использовать. Так называемая относительная энтропия задана формулой

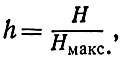
где H - энтропия данного кода, а Н_макс. - максимальное значение энтропии. Избыточность кода является дополнением к относительной энтропии:

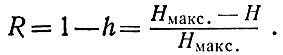
Поскольку энтропия является одновременно и количеством информации, то можно выразить избыточность сообщения и следующим способом:

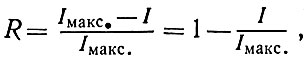
где I - эффективное содержание сообщения, то есть количество информации фактически переданной, а I_макс.- содержание, достигнутое при оптимальной передаче, например, в канале без шума и при наиболее экономичном использовании канала. Избыточность сообщения - это та часть решений при передаче, которая не является носителем действительного содержания сообщения.

Если уж приводить для иллюстрации какой-то популярный пример избыточности сообщения, то лучше всего указать на разговорный и письменный язык. Избыточность в языке состоит в растянутости и повторимости, обеспечивающих помехоустойчивость речи, возможность легкого понимания друг друга. Так, например, при разговоре в шумном зале или при обсуждении сложного вопроса речь требует большей избыточности. При малой избыточности, наоборот, концентрированность информации велика, велика и экономичность речи, то есть каждая фраза такой речи содержит что-то новое, что-то неожиданное, большую степень информации; однако при этом даже небольшая помеха приводит к большой потере информации. Простейшим видом избыточности является повторение. Более сложным видом ее является, например, применение так называемых контрольных кодов в передаче сообщений, о которых мы уже упоминали выше. Препятствием для концентрации информации как раз и является повышенный результат действия помех при пониженной избыточности. Кроме того, проблема избыточности сообщения связана также с проблемой времени. Степень отличительности в передаваемом сообщении зависит от времени. Можно понизить помехи и повысить отличительность при передаче сообщения тем, что мы растянем передачу на больший интервал времени, так что, собственно говоря, понизится пропускная способность передающего канала. Речь может идти о замедлении передачи или об использовании повторений, но и то и другое связано с избыточностью. Оба эти процесса облегчают понимание сообщения, прием его адресатом, что известно из процесса обучения; учебный материал лучше усваивается тогда, когда изложение ведется либо достаточно медленно, либо если трудные места изучаемого повторяются в различном виде.

Избыточность сообщения можно сводить к нулю при пользовании оптимальным кодом. При неравномерном распределении вероятностей символов и при наличии их внутренней вероятностной связи (корреляции) уменьшается относительная энтропия и возрастает избыточность сообщения. При создании текста мы делаем меньше выборов, чем число букв в тексте, так как мы действуем в рамках грамматических правил образования слов и предложений. Только примерно от ¹/₄ и до ¹/₃ числа букв мы можем выбирать произвольно: мы можем выбрать данные буквы или не выбрать их. Следовательно, при оптимальном коде мы могли бы выражаться втрое или вчетверо короче. Любая комбинация букв здесь создавала бы слово, полное смысла, так как все буквы и комбинации их встречались бы одинаково часто и каждая таблица букв могла бы годиться для кроссворда. Однако при обычном общении людей избыточность всегда имеет место, она имеется в каждом разговоре, в газетном языке и в научной литературе. Каждый национальный язык имеет значительную степень избыточности. Как уже было сказано, избыточность имеет не только отрицательные, но и положительные, полезные стороны. Она обеспечивает возможность понять друг друга, возможность исправить ошибки, получившиеся при передаче, тогда как при нулевой избыточности ошибки при передаче сильно искажали бы конечное сообщение.

Избыточность можно снизить путем перекодирования, путем изменения статистической структуры сигнала. Так, например, Нейдхардт¹ указывает, что в телевидении можно снизить избыточность путем уменьшения скорости развертывания передаваемого образа в тех местах, где сконцентрировано наибольшее информационное содержание, и путем ускорения развертывания в тех частях, где имеются свободные места и где можно эти промежутки интегрировать во времени. Если переходные вероятности между элементами одинаковы, нет взаимозависимости символов, то корреляция между ними нулевая. Если же, наоборот, они различны, то это дает экономию передачи и уменьшает избыточность. При передаче информацию несет только часть сигналов, остальные сигналы избыточны; в полезной части сообщения одна и та же информация может содержаться несколько раз, что дает возможность дальнейшего сжатия сообщения. Нейдхардт различает холостую (бесполезную) и полезную избыточность. Из неизбыточного сообщения нельзя изъять ни один знак, не изменяя этим его смысл. Если мы хотим установить избыточность сообщения, то мы убираем из этого сообщения знаки до тех пор, пока это не лишает сообщение понятности, то есть пока оно не теряет своего смысла. В противоположность холостой избыточности полезная избыточность обеспечивает или же и повышает верность передачи сообщения, и, наоборот, появление холостой избыточности не повышает ясности сообщения.

¹ (См. Р. Neidehardt, Einf?hrung in die Informationstheorie, Berlin, 1958.)

Выявление избыточности печатного текста выполняется, например, с помощью так называемой ампутации текста, при которой из полной формы напечатанных букв убирают какие-то части, так что мы можем определить предел читаемости, а следовательно, и меру избыточности. Аналогичным образом эта мера применяется для определения видимости цветов с помощью так называемых псевдоизохроматических таблиц. На использовании (вернее на устранении) избыточности основана стенография, а также экономия времени при телеграфировании. Так, например, в телеграфном коде Морзе наиболее короткие знаки - точки - используются для буквы Е, чаще всех встречающейся в английском языке.

Наглядный пример использования избыточности для сжатия передаваемого текста приводит Мейер-Эпплер¹. Имеем текст, состоящий из 23 букв:

¹ (W. Meyer-Eppler, Informationstheorie, "Naturwiss.", № 15, 1952, S. 341.)

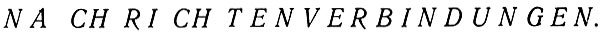
В этом тексте можно заменить чаще всего встречающиеся в немецком языке пары букв, то есть диграммы, отдельными реже встречающимися в этом языке буквами, а вместо этих букв текста ввести необычные пары букв. Так, например, пары

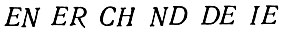
можно заменить буквами

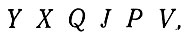
а вместо буквы V будем писать НС, так что путем такого перекодирования мы получим новый текст, состоящий уже только из 18 букв.

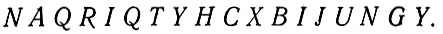
Другой пример с более высокой и более низкой избыточностью в коде приводит Черри¹:

¹ (C. Cherry, On Human Communication, New York, 1957, p. 186.)

Если бы мы закодировали буквы А, В, С и D только с помощью двух бинарных знаков, например, как

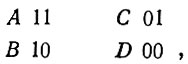
то этот код получился бы очень экономичным, имеющим малую степень избыточности. Однако в этом случае даже небольшая помеха привела бы к тому, что сообщение стало бы слишком неразборчивым. Если же мы закодируем эти буквы с помощью четырех бинарных знаков, например, так

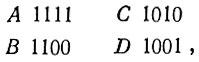
то код станет более избыточным, но он будет иметь большую помехоустойчивость. Если, например, помеха коснется одного знака (он исказится), то эту помеху можно обнаружить (но, конечно, не сразу же исправить ее). Так, например, при одной помехе код для A может измениться в 1110, 1101, 1011 (вместо 1111) или же 0111, то есть во всех этих случаях код А нельзя будет спутать с группой кодовых символов для В, С или D, как это может иметь место в случае двухзначного кода при одной помехе (когда получится 0 вместо 1 или 1 вместо 0). Конечно, например, группа 1110 может при одной ошибке получиться при искажении не только кода буквы A, но и кодовых букв В, С или D. Еще большая помехоустойчивость может быть получена при еще большем усложнении кода, при придании ему еще большей избыточности.

Правильное кодирование передаваемых и записываемых сообщений имеет большое значение для человеческого общества, которое поэтому и изыскивает все более экономичные способы кодирования сообщений. Сообщение можно расположить, например, в ряды, но более экономичным будет расположение сообщений в группы. Например, в телеграфной передаче каждой из 32 букв отведена какая-то единица времени, в телетайпе же введена более экономичная система, состоящая только из пяти единиц времени для всех 32 букв. Вместо 32 знаков здесь используется только 5 знаков. 32 знака управляются пятью двоичными шагами. Групповая компоновка использована также при написании чисел в десятичной системе. Совокупность всех сообщений о тысяче численных данных (чисел от 0 до 999) можно выразить только тремя цифрами. В противоположность этому расположение в ряд требовало бы тысячи знаков и выбора из тысячи возможностей. Поэтому прежнюю римскую цифровую систему, у которой было именно рядовое расположение цифр, заменили арабской цифровой системой. (Римская цифровая система состояла, собственно говоря, из ряда линий, но притом так, что для пяти линий ввели знак V, для десяти линий - знак X, для пятидесяти линий - знак L и т. д.)

Совокупность сообщений V требует не менее log_MV данных, если каждое данное касается одного решения из M возможностей. На этом принципе можно построить ограничение числа разрешающих шагов. Если, например, мы имеем 32 (карты (или буквы и т. п.), то вероятность того, что мы угадаем, какая карта вытянута из колоды, будет ¹/₃₂, и в среднем необходимо 16 раз гадать, прежде чем угадаешь правильно, какая карта вытянута. Однако, чтобы угадать это, достаточно иметь только пять ответов "да - нет" на пять вопросов, что соответствует числу log₂32.

Эти пять вопросов можно составить следующим образом:

1. Красная ли это карта? (Если "да", то это значит, что червовая или бубновая карта, "нет" - значит либо трефовая, либо пиковая карта.)

2. Червовая ли это карта (или бубновая)?

3. Фигура ли это? (При ответе "нет" это значит, что карта цифровая.)

4. Это карта из высшей половины (фигур или цифровых карт)?

5. Это четная карта из данной половины?

После пяти ответов на эти вопросы мы получим ответ, какая именно карта вытянута.

Таким образом, с помощью надлежащей упорядоченности можно добиться экономии и снижения избыточности. Хорошим примером низкой избыточности, приводимым Земанеком¹, является шрифт для слепых, в котором остается неиспользованным лишь небольшое пространство из шести полей одной буквы. Здесь избыточность составляет только 31,4%. В противоположность этому блочный типографский шрифт, где для одной буквы используется 35 полей карты, имеет сравнительно большую избыточность - 88,3%. Письменный шрифт имеет довольно большую избыточность, и он должен ее иметь хотя бы по той причине, что индивидуальные отклонения в начертании отдельных букв приводили бы при низкой избыточности к большей степени искажений. Как отмечает Земанек, только благодаря тому, что письменный шрифт имеет большую избыточность, получается, что аптекарь может прочитывать ^написанные врачами рецепты, которые для профанов совершенно непонятны. Стенография является, собственно говоря, сильно упрощенным письменным шрифтом с низкой степенью избыточности. Можно с уверенностью сказать, что избыточность существует не только в языке письма или речи, но и в языке нашего мышления (так называемый внутренний язык, по Теплову), и в мышлении, и познании вообще. Не исключено, что на основе математических исследований информации и избыточности мы придем к созданию универсального шрифта и языка для максимально экономичного кодирования научной информации. Само собой разумеется, что в зависимости от назначения данного научного сообщения степень избыточности в нем должна быть различной и, например, для научно-популярной работы нужна большая степень избыточности, чем для работы, предназначенной для специалистов по данному вопросу.

¹ (H. Zemanek, Ungewohnte Zahlen aus der Informations-theory, "Radiotechnik", № 6, 1954, S. 188.)

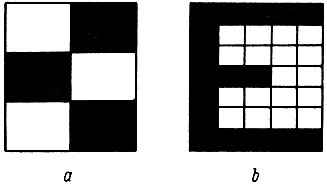
Рис. 6. Избыточность шрифта: а - шрифта для слепых, б - блочного типографского шрифта (по Земанеку)

В вышеназванной статье Земанек указывает, что в среднем в нашей речи избыточность составляет 75% (различные национальные языки имеют, конечно, различную степень избыточности, причем сравнительно наименьшую избыточность имеет английский язык). Страница книги, содержащая 500 - 2500 букв, содержит не 2500 - 12500 двоичных единиц информации, а только лишь 600 - 3000 этих единиц. Если книга имеет 500 страниц, то в ней содержится 10⁶ двоичных единиц информации. Среднее количество томов в каждой из десяти крупнейших американских библиотек было в 1850 году 2·10⁴, в 1900 году - 2·10⁵, в 1950 году - 2·10⁶, гак что можно ожидать, что в 2000 году среднее количество томов в таких библиотеках составит примерно 2·10⁷. Количество двоичных единиц информации, находящихся в этих книгах, возрастет соответственно с 2·10¹⁰ до 2·10¹². Исходя из этого, Земанек считает, что данное количество книг могло бы служить базой для составления приблизительной картины роста человеческих знаний. Конечно, тут Земанек измеряет информацию только технически - по количеству букв, но не семантически, то есть по смыслу и по плотности информационного содержания. В этой статье Земанек пытается также определить верхний предел объема информации, могущего быть использованным одним читателем в течение всей его жизни, и этот объем не превышает, по Земанеку, 5·10¹⁰ двоичных единиц информации.

Рост человеческого познания и накопление информации памятью также делается возможным именно благодаря бессознательному использованию избыточности. Наша память производит сжатие информационного содержания зафиксированных ею сообщений, и она снижает их избыточность, сохраняя только самое существенное из сообщений. (К этому вопросу мы еще возвратимся в конце настоящей книги.) По-видимому, следует считать память системой обусловленных вероятностей. Чем теснее связь запомнившихся содержаний, тем больше упорядоченность в памяти и тем меньше ее избыточность.

Вопросы о сжатии информационного содержания в сообщениях, о наиболее целесообразном кодировании сообщений и о снижении избыточности в мышлении и памяти имеют важное значение для роста человеческого познания. Уже само возникновение второй сигнальной системы означало экономичность, так как вторичные сигналы - слова - являются обобщением большого количества первичных сигналов - восприятий. Далее была достигнута экономия, например, путем введения различных удобных способов кодирования научной информации, как, например, созданием математических и прочих символов и книгопечатания. Речь идет здесь, конечно, не только о внешних формальных средствах, вопрос об избыточности и экономичности касается также и содержания научной информации.

В настоящее время, например, проблемой, имеющей значение для дальнейшего непрерывного развития научного познания, становится чрезмерное возрастание числа научных книг, что связано с большой степенью избыточности в научных книгах, то есть с тем, что в различных книгах идеи повторяются и читатель теряет много времени, так как он вынужден читать в изучаемых книгах такое, что он и без того знает и что не дает ему новой информации. Причем потеря времени на чтение уже знакомого текста непропорциональна выигрышу от закрепления в памяти информации, полученной уже ранее. Поэтому было бы желательно провести какую-то унификацию, централизацию, концентрацию и контроль книжного фонда, чтобы можно было обеспечить лучший учет, обзор научной литературы и снизить избыточность. Как остроумно указывает польский писатель Станислав Лем в своей книге "Магелланово облако", при нынешнем росте книжной продукции дело может дойти до того, что через какое-то время каждому второму человеку в мире придется стать библиотекарем и земной шар превратится в гигантскую библиотеку. Поэтому необходимо найти способы улучшения хранения и переработки научной информации путем внедрения в библиотечное дело электронных вычислительных машин. Введение информации в эти машины было бы значительно более экономичным, чем в книги, и это дало бы значительное снижение избыточности в научных книгах. С помощью этих машин можно было бы также экономично обрабатывать информацию таким образом, что будет выявляться гомоморфизм в научных сообщениях, а это приведет к снижению избыточности, ибо приведет к исключению того, что во многих научных работах является одинаковым и повторяющимся. Одновременно это объединяло бы то подобное, что имеется в работах различных дисциплин.

Собственно говоря, объективная реальность составляет для нашего познания совокупность сообщений различной длины и различной степени отличительности. Совокупность этих сообщений - это материальный пространственно-временной континуум, из которого мы в процессе познания совершаем определенный выбор. Вещи и процессы вокруг нас, или, выражаясь словами Минковского, мировые линии образуют отдельные сообщения, выборы из совокупности сообщений, передаваемых в наше сознание, в наш мозг и здесь декодируемых более или менее успешно в зависимости от степени нашей опытности, от совершенства нашего способа отражения и т. д. Поскольку невозможно при этой передаче сообщений полностью устранить шум, обусловленный ограниченностью наших познавательных способностей, информация в нашем познании может приближаться к максимальной информации только асимптотически и точно так же избыточность в нашем познании может только асимптотически приближаться к нулевой избыточности.

На первый взгляд существует некоторая ограниченность в повышении информации и в снижении избыточности в нашем познании. Нулевая избыточность могла бы быть достигнута тогда, когда эффективное содержание сообщения было таким же, как содержание, которое может быть нами получено при оптимальном использовании канала, что возможно было бы, например, при полном отсутствии помех. Помехи в передаче сообщений можно уменьшить применением избыточности, путем использования более длительного времени для передачи наряду с некоторыми другими способами борьбы с помехами. Между скоростью передачи и помехами должна, следовательно, существовать определенная зависимость. Нельзя, например, полностью устранить разрыв во времени между входом и выходом при передаче сообщения. Самый быстрый процесс передачи информации может ведь происходить только со скоростью света (если иметь в виду только физическую скорость передачи сообщения; в теории информации скорость передачи сообщения измеряется числом переданных двоичных единиц информации в секунду).

Однако развитие познания является доказательством того, что нет никакого абсолютного предела нашего познания, имеются только пределы относительные, исторические. Человек приобретает все более совершенные знания об объективной реальности, и его информация возрастает, а избыточность в его мышлении и познании убывает. Производится конденсация информации, причем это не связано с повышением помех и аварийности, а обеспечивается способностью к обучению и памятью. По мере развития общества, от поколения к поколению человек все лучше осваивает более экономичные коды для передачи сообщений, фиксации и хранения их в мозгу.