2. Моделирование накопления информации

Источник сообщений высылает сообщения, а адресат отображает на стороне приема эти сообщения, прошедшие через канал и несколько искаженные аддитивными помехами. Подобно этому в процессе познания объект отображается субъектом с некоторым огрублением, с некоторой энтропией. Развивающееся познание сохраняет полученную информацию об объекте в памяти, и при дальнейших отображениях этого объекта информация возрастает и энтропия убывает; можно оказать, что память имеет возможность ограничивать шум. Факт накопления информации в памяти дает возможность понимать процесс развивающегося познания как процесс обучения.

То, что можно квантовать информацию и энтропию, представляет возможность создать очень упрощенную, ограниченную модель отображения и памяти путем расположения максимальной информации и максимальной энтропии в определенную систему. Имеем следующую классификацию:

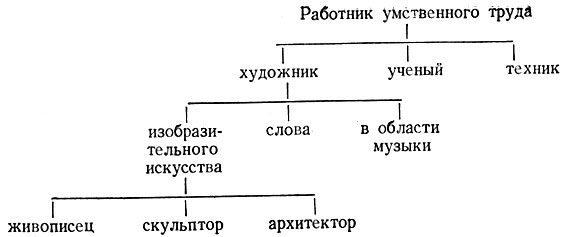
Если мы должны решить, куда отнести, например, Николая Алеша, о котором нам известно, что он относится к работникам умственного труда, мы сначала решаем, к какой части первой строки он относится (первый разрешающий шаг), затем мы находим его место во второй и в третьей строках. Если мы узнаем, что он относится к художникам, то мы дальше находим, к какой группе художников он относится, и после того, как мы установили, что он относится к художникам изобразительного искусства, мы дальше устанавливаем, что он является живописцем. Таким образом, при каждом разрешающем шаге мы встречаемся с некоторой неопределенностью. Вначале мы могли бы вынести суждение, что "Алеш является работником умственного труда (вида х)", где вместо переменной можно подставить три различных аргумента с одинаковой вероятностью. Конечная схема случаев и их вероятностей такова:

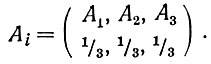
Определив энтропию по формуле

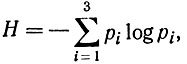
получим

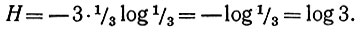
Дополняя функцию суждения правильным аргументом "художник* мы получим суждение "Алеш - работник умственного труда (вида "художник" )" или проще "Алеш - художник", которое можно преобразовать в следующую функцию суждения: "Алеш - художник (вида х)" опять-таки с тремя аргументами. После правильной (Подстановки получим суждение "Алеш - художник в области изобразительного искусства", отсюда функция суждения "Алеш - художник в области изобразительного искусства (вида x)" с тремя аргументами. Наконец, мы получим суждение "Алеш - живописец". Таким образом, для получения наивысшей возможной информации в данной ограниченной системе нужно выполнить три разрешающих шага, в каждом из которых надо выбрать одну из трех возможностей. Следовательно, в функции суждения "Алеш - работник умственного труда (вида х)" информация нулевая и по сравнению c максимальной информацией, содержащейся d суждении "Алеш - живописец", здесь (в первом из этих суждений) максимальна энтропия, равная H = log 3 + log 3 + + log 3 = 3 log 3. Матричная таблица информации и энтропии суждений или функций суждений нашей системы выглядит так:

Связь информации и энтропии в этой системе задана уравнением

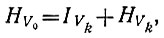
следовательно, сумма информации и энтропии -постоянна и представляет собой максимальную энтропию или максимальную информацию в системе. Информация в любом суждении системы задана уравнением

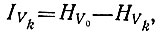
то есть в виде разности между максимальной энтропией системы и энтропией суждения данной ступени. Максимальную информацию в суждении υ₃ можно таюке считать информацией переданного сообщения, мерой информации в дальнейших суждениях для различной степени изображения сообщения получателем в процессе обучения, то есть, собственно говоря, для различной степени действия шума. Суждение υ₃ можно считать принятым сообщением, переданным по каналу без шума и информация которого, следовательно, не уменьшилась в ходе передачи: такое суждение максимально определено, энтропия его нулевая. Шкала от Vυ₀ до υ₃ может представлять последовательный процесс обучения, простой подъем познания, когда в памяти остается уже информация, полученная из сообщения предшествующей ступени. Иначе говоря, суждение "Алеш - живописец" включает в себя суждение "Алеш - художник в области изобразительного искусства", которое в свою очередь включает в себя суждение "Алеш - художник".

Если в нашей информации о том, кем является Алеш (согласно приведенной выше модели), есть какая-то ненадежность вследствие забывания, то можно эту ненадежность выразить с помощью угла φ. Косинус ср выражает соответствующую информацию, а синус φ - неизвестную, потерянную информацию или ненадежность, энтропию. Если мы, например, имеем информацию "Алеш - художник", то эта информация равна 2 log 3, что можно выразить с помощью разделения на известную и неизвестную составляющие (см. вывод предыдущей главы) при φ = 30° и, следовательно, как шоинус 30°. Приведенную выше таблицу нашей модели можно дополнить следующим образом:

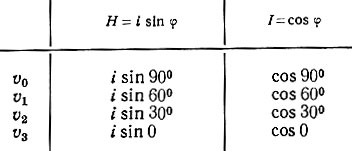
I_макс. - здесь соответствует сумме i синуса и косинуса, то есть e^iφ

Это сильно упрощенная модель, в которой количество максимальной информации задано конечным числом ограниченной системы с каким-то началом и концом. В действительности суждение "Алеш - живописец" не является последней ступенью и требует дальнейшего определения, то есть того, каким именно живописцем является Алеш. Но и в обратном направлении первая ступень не задается суждением "Алеш - работник умственного труда", так как этому суждению могло предшествовать другое "Алеш - человек" и еще далее: "Алеш - живое существо" и т. д. Действительность невозможно исчерпать и определить конечным числом шагов, анализ продолжается все глубже, познание неисчерпаемо. Далее необходимо обратить внимание на то, что в нашей модели принято для упрощения, что вероятности в отдельных ступенях независимы друг от друга. Точнее была бы более сложная модель, отдельные cтупени которой взаимозависимы; тогда матрица выглядела бы несколько иначе. Эта модель лучше отображала бы факт сохранения информации в памяти, но для данной нашей цели нет надобности вводить такую точную модель.

Полная информация изображена на отдельных фазах "развития" указанной системы изображения с уменьшающейся неполнотой (υ₀, υ₁, υ₂, υ₃). Меру определенности или неопределенности в принятых сообщениях в процессе обучения можно, следовательно, привести во взаимосвязь со временем. Максимальная энтропия в отображении в ходе указанного процесса получения опыта была бы в момент t₀, когда получено первое сообщение в виде суждения υ₀. Минимальная энтропия была бы в момент t₃. Если I_макс. = 3 log 3, то тут также задано число разрешающих шагов, необходимых при действии от I_макс. и число альтернатив при каждом из этих шагов. Получение информации - опыта- здесь корреспондируется со временем. Если мы введем в нашу модель наряду с неопределенностью еще и неистинность (ошибку), то это означало бы, что познание может пойти и по .неправильному пути, как в лабиринте. Конкретно это означало бы, например, что мы определим, что "Алеш - техник". Тогда путь к максимальной информации мог бы быть более длинным в зависимости от числа необходимых обратных шагов. Ошибочный путь можно изобразить временем обратного направления, относительно t₀, так как он требует обратных шагов. Например, неправильное суждение "Алеш - техник" соответствовало бы тогда моменту t_-1, так как оно требует одного обратного шага к t₀. В нашей модели этому случаю соответствовало бы отрицательное количество информации, а энтропия была бы больше, чем 3 log 3.

В нашей модели информационной системы можно выразить и избыточность. Избыточность сообщения υ₀ наибольшая (R=l), избыточность сообщения υ₃ - наименьшая (R = 0). Утерянная информация здесь соответствует энтропии (или потерянному времени). Все сообщения имели бы в этом случае одинаковую продолжительность (имели бы одинаковое число сигнальных элементов), но различную плотность информации, то есть неодинаковое количество информации, приходящейся ,на один сигнальный элемент. Если

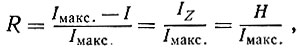
то можно выразить избыточность отдельных сообщений следующей таблицей:

Обозначив один сигнальный элемент сообщения через x, а полезный сигнал, несущий информацию, - через x, получим следующую таблицу:

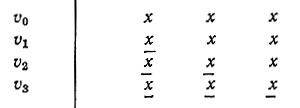
Можно изобразить сообщения также посредством четырех концентрических кругов, представляющих различные степени определенности и на которых обозначено число выбранных элементов и их вероятности (исходя из полной классификации с диапазонами в 3, 9 и 27 элементов), как это показано на рис. 13.

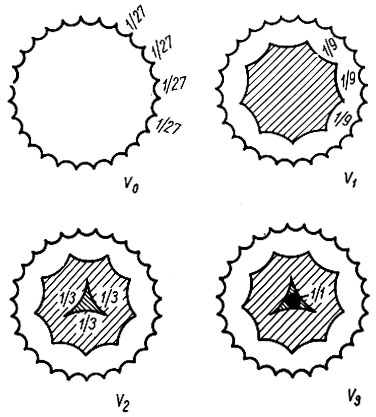
Pис. 13. Изображение информации суждения формой

Получив максимальную информацию в нашей ограниченной модели, то есть оптимальную систему отображения, мы могли бы отсюда построить более высокую систему отображения, взяв за основу эту максимальную информацию, I_макс. в системе отображения I было бы Iмин. в системе II и тогда t₃ в системе I было бы t₀ (В системе II. Образование все более мощных систем отображения и является существом развития познания. Время в развитии познания находится в тесной связи с ростом информации. Полученная информация означает снижение временной задержки, так как для повторного получения информации (воспроизведения ее) времени не требуется оно мгновенно и всегда находится в готовности. Абсолютная истина, совокупность всей информации об объективной реальности представляет собой гипотетическое отображение, над которым уже нет более высокого, более полного отображения и где отпадает необходимость в течении времени для информации. Конечно, такая информация может быть достигнута лишь в ходе бесконечной эволюции познания, то есть практически никогда. Рост информации в развитии познания, возможный благодаря существованию памяти, соответствует, следовательно, определенной временной характеристике.

Нулевую энтропию и максимальную информацию можно было бы достичь лишь тогда, когда информация об объективной реальности была бы конечной и исчерпываемой. Однако развитие познания является не замкнутым процессом, поэтому никогда нельзя достичь того, чтобы энтропия была нулевой. В нашей ограниченной конечной модели отображающей системы мы исходили из постоянной суммы "информации и энтропии. Для незамкнутой системы отображения можно было бы считать постоянной скорее произведение информации и энтропии, а не их сумму. Следовательно,

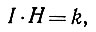
и отражением этой функции была бы вместо прямой равноосная гипербола. Чем больше убывала бы энтропия в этой системе, тем больше возрастала бы в ней информация, мера которой асимптотически приближалась бы к бесконечности, но никогда не могла бы достичь ее, так как мы исходим из того, что энтропия в познании никогда не бывает в конечном времени нулевой.

Ограниченная система отображения, описываемая, например, вышеуказанной моделью, может быть преобразована нами в неограниченную, если мы примем, что начало и конец процесса роста информации находятся в бесконечности. Тогда информация в отображении могла бы возрастать по мере течения времени, и этот рост был бы бесконечным. Абсолютная истина представляла бы собой тогда отображение с энтропией, приближающейся к нулевой, заданной, так как вероятность одного случая равна единице, а остальных случаев - нулю. Нулевую неопределенность в сообщении можно предположить на стороне входа, у источника сообщений - у объективной реальности. Следовательно, такой случай представляет только бесконечную, вечную и единую материю в совокупности всей ее материальности и различия форм движения и ступеней упорядоченности¹.

¹ (В указанной простой модели процесса обучения можно было бы использовать наряду с понятиями "информация", "энтропия" и "избыточность" также и другие понятия теории информации, так что можно было бы создать все более сложные, все более тонкие модели гносеологического -канала.)