3. Некоторые исходные положения для дальнейших исследований

а) Мир Минковского и память

Для отображения накопления информации можно использовать также геометрическую модель памяти. Память (которую мы понимаем здесь не узко - как фиксирование того, что дано нашими органами чувств, а как совокупность знаний как индивида, так я всего общества) может рассматриваться как пространство информации. Сохранение происшедших ранее событий в памяти, не только событий внешнего мира, но и внутренних событий, какими является переработка опыта, окажется тогда тесно связанным с проблемой времени.

Представляя события как точки в евклидовом пространстве, мы получим, например, точку А, заданную тремя размерами:

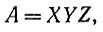
расстояние которой от начала координат задано длиной d по формуле

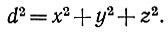
В пространстве - времени Минковского расстояние от начала координат задано уравнением

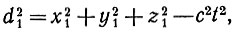
где с - скорость света, a t - время. Определив u = ict,где

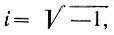
можно ввести

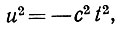
так что мы получим

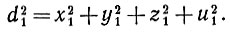
Точка А в пространстве - времени Минковского будет тогда задана как

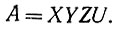
Аналогично этому можно представить себе точкой также информацию о событии, так как к точкам в пространстве события можно отнести соответствующие точки в пространстве информации. Однако в определенном сведении, преобразованном в опыт, можно отразить и информацию о двух или большем числе событий. Если мы имеем событие А в момент t₁ и событие В в момент t₂, то благодаря памяти мы можем иметь информацию об обоих событиях одновременно, что можно записать в виде

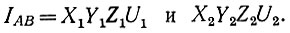
Таким образом, в определенном сведении может храниться информация о прошлых событиях. В какой-то выбранной нами гносеологической единице, например в фразе определенной длины, может содержаться информация о различном количестве событий, то есть сообщение может иметь различную информационную плотность. Иначе говоря, в сообщении определенной длины может быть различная мера полезной информации и избыточности.

Гипотетическое одноразмерное существо (например, в виде отрезка определенной длины), движущееся по двухразмерной площади, на которой имеются расположенные по-разному точки, могло бы воспроизводить (если оно обладает памятью) распределение точек в отдельных положениях, через которые оно прошло, и оно могло бы сразу восстановить двухразмерную картину в своем одноразмерном "мозгу". Аналогично этому обстояло бы дело с гипотетическим двухразмерным существом, прошедшим через трехразмерное пространство. Опять-таки аналогично этому трехразмерное существо с трехразмерным мозгом, наделенным памятью, движущееся по четырехразмерному пространству, способно уловить и восстанавливать в памяти все его события, причем одновременно, без распределения во времени, сразу. Таким образом, в памяти информация будет укладываться, по-видимому, в четырехразмерном коде. На основе памяти мы можем восстановить одновременно информацию о событиях, значительно удаленных друг от друга в пространстве или во времени. Следовательно, память - это способность уплотнять информацию. Если в единице обычного солнечного Времени можно воспроизвести в памяти различное количество информации, то это означает, что тут целесообразно использовать шкалу неравномерно текущего времени, о котором мы говорили в первом параграфе настоящей главы. Если в этой единице времени в нашем распоряжении имеется большее количество информации, чем среднее определенное количество, которое было бы в случае роста памяти, то здесь мы могли бы говорить об относительной дилатации времени, о том, что по мере развития оно (время) течет все медленнее. Единица времени нашего познания (которое можно назвать гносеологическим временем аналогично тому, как говорят о биологическом времени) измерялась бы тогда не звездными событиями или вращением Земли, как в отношении обычного солнечного времени, а событиями нашего познания - зафиксированной информацией. Так можно будет выразить емкость (пропускную способность) памяти или познания.

Минковский называет пространственную точку, находящуюся в какой-то точке времени, мировой точкой. Изображением существования такой мировой точки будет кривая, называемая мировой линией, точки которой можно однозначно отнести к параметру t от - ∞ до + ∞. Весь мир можно разложить на такие мировые линии - события. Такими мировыми линиями можно аналогичным образом изобразить и информацию о событиях. Ведь чем является человеческая социальная память, совокупность общественного познания, если не моделью мира, пространства - времени? Как говорит Минковский, подобно тому как в пространстве имеется бесконечно много плоскостей, так и в пространстве - времени имеется бесконечно много пространств. Этому подобна гипотетическая универсальная память, включающая в себя все развитие, всю эволюцию познания. Гипотетическая абсолютная истина состояла бы из бесконечного количества относительных истин отдельных сведений или из памяти отдельных индивидов.

Мы не намерены детально описывать здесь всю модель мира Минковского, но хотим лишь обратить внимание на важнейшие черты ее. В пространстве - времени Минковского можно как угодно определять временную ось, как угодно раскраивать мир.

"Субстанция, находящаяся в любой мировой точке, - писал Минковский, - может при особом определении рассматриваться всегда как находящаяся в покое относительно пространства и времени¹". Для всех скоростей здесь имеется верхний предел скорости света с. Мир Минковского - это формация, разделенная t = 0 в двухчашечный гиперболоид. Гипербола является здесь изображением мировой линии, представляющей движение, которое для t = + ∞ и t = - ∞ асимптотически приближается к скорости света.

¹ (H. Minkowski, Raum und Zeit, з: Lorentz - Einstein - Minkowski, Das Relativitätsprinzip, Leipzig, 1922,5.58. (Русск. перев.: Г. Минковский, Пространство и время; в: Г. А. Лоpеяц, А. Пуанкаре, А. Эйнштейн, Г. Минковский, Принцип относительности. Сборник работ классиков релятивизма, М., 1935.))

Можно создать экспериментальную гипотезу, согласно которой в модели мира Минковского различным величинам скорости будут соответствовать различные величины плотности событий, или различные плотности информации в памяти. При малой плотности информации время протекало бы равномерно и этому соответствовала бы большая избыточность в полученном сообщении о мире. При нарастающей плотности информации время протекает неравномерно, оно дилатирует и соответствует этой убывающей избыточности ;в познании. Предельная скорость света соответствовала бы предельной плотности информации и нулевой избыточности.

Основатель термодинамики Карно говорил об идеальной тепловой машине, которую, конечно, практически невозможно создать, так как это означало бы создать перпетуум-мобиле первой ступени. Все же его идеи стали основой термодинамики. Подобно этому физика газов опирается на плодотворную идею идеального газа, в действительности не существующего. Аналогично этому можно было бы говорить, например, об идеальном получателе информации (этим адресатом могла бы быть, например, гипотетическая идеальная логическая машина), в памяти которого уложена вся информация о мире и который, следовательно, знал бы абсолютную истину, хотя мы знаем, что это невозможно.

Карно доказал, что работа, выполняемая тепловой машиной, не равна всей поданной в машину тепловой энергии, а часть этой энергии расходуется на охлаждение. Полученная работа равна разности между поданным теплом Q₁ и неиспользованным, отведенным теплом Q₂, то есть работа меньше подведенного тепла. Так называемый тепловой коэффициент полезного действия машины η равен отношению полученной работы к подведенному в машину теплу:

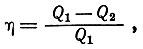
и он (к. п. д.) всегда меньше единицы, то есть 100%, что могло бы быть достигнуто при наличии идеальной машины, то есть перпетуум-мобиле.

При передаче информации происходит потеря ее из-за помех. Количество утерянной информации равно разности между количеством переданной информации и количеством полученной информации. Избыточность передачи информации выражается формулой

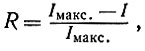
где I_макс. - информация, высланная и принятая в оптимальном случае, I - информация, принятая, эффективная. Дополнением к избыточности, бесполезности в передаче является

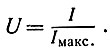
Потерянная, неиспользованная информация I_z задана разностью между максимальной и полезной информацией: I_z = I_макс. - I, так что

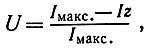
что можно считать подобием коэффициента полезного действия η Карно. Максимальная полезность U_макс. имеет место при I = I_макс., или при I_z = 0, а минимальная полезность будет при I = 0. Максимальная полезность соответствует минимальной избыточности по уравнению

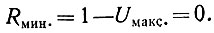
В этом случае сообщение передано наиболее экономично, с максимальной скоростью передачи и с максимальной конденсацией информации, следовательно, с минимальным числом сигналов, с максимально экономичным кодом; сообщения имеют здесь минимальную длину.

В мире Минковского мировые линии покоящихся материальных точек, точек с нулевой скоростью, изображены как параллели с временной осью. Этим мировым линиям соответствовали бы в аналогичной модели памяти (отражения мира) сообщения, переданные с максимальной избыточностью, то есть сообщения, воспринимаемые системой с минимальным опытом, с нулевым запасом информации или с минимальной пропускной способностью приема. Сообщения, принимаемые системой с растущей памятью, изображались бы здесь прямыми или кривыми, отклоняющимися от этой оси. Сообщения при передаче с максимальной полезностью (U = l) и со скоростью передачи С изображались бы как параллельные со второй осью. Это были бы сообщения идеального адресата, при передаче которых не было никакой потери информации, при отсутствии помех и когда сообщения могут иметь нулевую избыточность.