5. Поиск по дереву и игра в шахматы

В современной математике слово граф имеет особое значение. Граф состоит из вершин, соединенных между собой ребрами; каждой вершине приписывается определенный смысл. Каждое ребро указывает на определенное отношение между парой соединяемых им вершин. Например, вершины могут представлять собой города, тогда соединяющие их ребра указывают на такие пары городов, между которыми проложена дорога. В этом смысле обычная карта представляет собой граф, но положения вершин в таком графе особого значения не имеют - важен лишь характер их взаимного соединения.

В некоторых приложениях ребра, соединяющие вершины графа, рассматривают в двух направлениях. Например, если граф показывает дороги, соединяющие города, то естественно, что эти дороги никогда не являются односторонними, и из того факта, что город А соединен с городом В, следует, что и город В соединен с городом А. Если бы мы представили с помощью графа маршруты автомобильного движения в пределах города, то этот граф имел бы иной характер. В городе многие из связей представляют собой улицы с односторонним движением, поэтому соответствующие соединительные ребра в графе необходимо пометить стрелкой. Улицу с двусторонним движением тогда можно представить парой ребер, помеченных стрелками, указывающими в противоположные стороны. На рис. 5 показан граф, изображающий улицы (с указанием направления движения) в небольшом городе Англии.

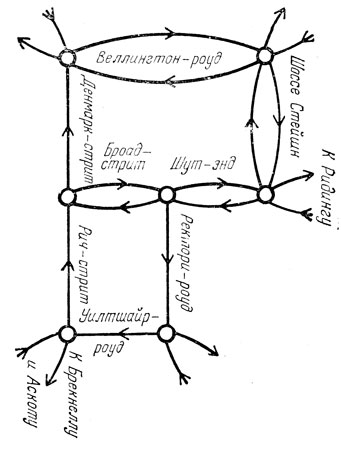
Рис. 5. Главные улицы в центре Уокингема (Беркс), представленные в виде графа

Особый интерес представляет граф специального типа, называемый деревом. Он имеет одну вершину, которую нельзя достичь ни из какой, другой вершины; эта вершина называется корневой. У нее имеется некоторое число дочерних вершин, непосредственно достижимых из нее (в случае бинарного дерева имеются две такие дочерние вершины), у них в свою очередь также есть дочерние вершины и т. д. Любое дерево, которое может быть нарисовано или представлено в памяти вычислительной машины, должно иметь конечный размер, т. е. у него должны быть вершины, не имеющие дочерних. Последние называются терминальными вершинами, или листьями графа.

На рис. 6 показано дерево, вершины которого изображены прямоугольниками. Деревья, представляющие системы обработки данных, в отличие от реальных деревьев обычно изображают корнем вверх. На ребрах графа, показанного на рис. 6, нет стрелок, хотя по смыслу они асимметричны, - общее расположение показывает, как соединены вершины.

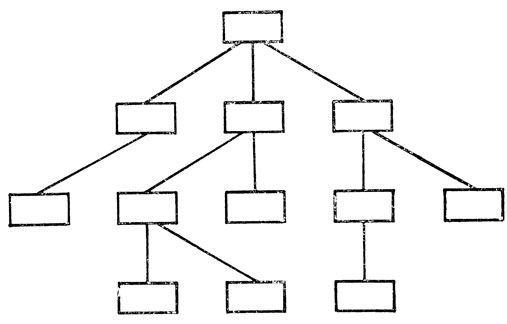
Рис. 6. Древовидная структура

В проблеме искусственного интеллекта деревья представляют особый интерес; тому имеется несколько причин. По-видимому, главная из них рассмотрена в гл. 13 (приложение 1). Сейчас же мы остановимся на другой причине. Дело в том, что любой дискретный процесс принятия решений в заданной детерминированной системе может быть представлен в виде дерева. Если корень дерева соответствует начальному состоянию системы, то его дочерние вершины соответствуют состояниям, которые могут быть результатом применения различных операций из числа имеющихся. Далее, для каждой из таких дочерних вершин существует некоторое множество возможных операций, каждая из которых приводит к новому состоянию, представляемую внучатыми вершинами, и т. д.

Широкий набор процедур решения проблем (включая методы доказательства теорем, рассмотренные в последних двух главах) может быть представлен как прохождение по дереву, у которого один или более листьев соответствуют успеху в доказательстве теоремы. Эвристики представляют собой способы определения того выбора, который следует сделать в каждой вершине, чтобы попытаться достигнуть одного из листьев с меньшими затратами труда, чем это было бы при достижении листьев посредством полного перебора имеющихся вариантов. В нетривиальных задачах полный перебор следует исключить, поскольку это приводит к комбинаторному взрыву. Возможность возвращения, которая является существенной особенностью универсального решателя задач, легко отображается в дереве как возвращение в предыдущую вершину на данном пути, после чего выбирается другая дочерняя вершина.

Представление методов решения задач в виде исследования деревьев весьма полезно (Нильсон [1]), но, как было показано, эти методы можно анализировать и другими способами. (В большинстве случаев графы используются в математике при выводе результатов, которые можно было бы получить и иначе, однако метод теории графов обычно оказывается наиболее элегантным и понятным.)

Игра в шахматы и другие игры с помощью вычислительных машин - проблемы, которым в работах по искусственному интеллекту уделяется большое внимание. В программах, оказавшихся успешными для ведения целого ряда игр, явным образом обследуется дерево, которое указывает возможные продолжения игры из заданной начальной ситуации. Для сокращения возникающего при этом перебора необходимо ввести новый набор эвристических принципов.

Шахматы

Древняя игра в шахматы бросает несомненный вызов ученым, работающим в области искусственного интеллекта. Однако еще до появления электронных вычислительных машин предпринимались попытки построить автоматы для игры в шахматы. Один из таких автоматов (или то, что по идее должно было стать таким автоматом) был создан фон Кемпеленом примерно в конце XVIII в. и получил название мейзелского шахматного автомата. Он вызвал огромный интерес среди образованных людей того времени, но никто не мог тогда с уверенностью сказать, действительно ли это гениальный автомат или просто ящик, в котором прячется карлик или ребенок, способный играть в шахматы на достаточно высоком уровне. Об этом устройстве писал Эдгар По, который считал, что оно не могло быть автоматом, поскольку порою выигрывало, а иногда - проигрывало. Если бы это был автомат, рассуждал По, то он должен был бы либо всегда выигрывать, либо всегда проигрывать.

Аргументация По, конечно, была необоснованной, но вывод его оказался правильным - "автомат" в самом деле скрывал в себе живого игрока небольшого роста. Настоящий автомат для игры в шахматы был изготовлен Торресом и Кьюведо в 1914 г. Он демонстрировался в испанском павильоне Международной выставки в Брюсселе в 1958 г. Однако этот автомат играл лишь начиная с позиции, в которой большинство фигур уже отсутствовало и оставались лишь два короля и ладья, принадлежащая автомату. В этой позиции автомат всегда выигрывал (существует алгоритм, использование которого гарантирует выигрыш при этих обстоятельствах). В автомат был встроен проигрыватель с миниатюрной граммофонной пластинкой; когда автомат выигрывал, на пластинку опускался звукосниматель - и раздавался победный звук.

С появлением вычислительных машин возникла возможность создания настоящего автомата для игры в шахматы. Проблему написания необходимой для этого программы исследовали Тьюринг, Стречи и Шеннон [2] (см. обзор Гуда [3], в который включены и работы последних лет).

Принципы работы, предложенные каждым из названных исследователей, и последующее воплощение их в действующих программах опираются на исследование дерева возможных продолжений игры. Его называют деревом просмотра возможностей. Корневая вершина такого дерева представляет текущую конфигурацию фигур на шахматной доске, а программа производит выбор хода. В середине шахматной партии у игрока обычно имеется около тридцати возможных вариантов следующего хода. Возникающие в результате их перебора конфигурации могут быть представлены как дочерние вершины для данной корневой вершины.

В каждой из дочерних вершин возможно около тридцати ответов противника, так что для изображения результирующих конфигураций потребуется еще около 900 вершин и т. д. Дерево быстро "разрастается". Существуют два типа вершин. Одни, наподобие корневой вершины, представляют конфигурации, в которых ход за программой; они называются альфа-вершинами. Вершины другого типа, представляющие конфигурации, в которых ход за противником, называются бета-вершинами. Последующие уровни такого дерева возможностей заняты по очереди альфа- и бета-вершинами.

Если бы дерево можно было обследовать полностью, т. е. вплоть до всех листьев, представляющих все возможные окончания в данной игре, то имелась бы возможность выбрать ход, обеспечивающий для машины выигрыш независимо от реакций противника^*. В действительности же полный просмотр всего дерева невозможен. Шеннон установил, что для обследования всего дерева в середине шахматной игры потребуется 10⁹⁰ лет машинного времени - в предположении весьма быстродействующей вычислительной машины. Если быстродействие такой машины увеличить еще в миллион раз, то и при этом потребовалось бы 10⁸⁴ лет - тоже слишком много. Эффект комбинаторного взрыва проявился бы здесь со всей силой, так что о полном просмотре дерева не может быть и речи.

^* (Если, конечно, такой ход существует! - Прим. перев.)

Вместо полного просмотра дерева в программах игры в шахматы обследуется лишь небольшая его часть. В таком случае обычно говорят, что дерево подвергается подрезке. Простейший метод подрезки - обрыв дерева на определенной глубине, т. е. просмотр вперед на некоторое фиксированное число полуходов (полуход - это ход одного из игроков). Нельзя сказать, что это хороший метод игры, но даже при использовании других методов допустимую глубину ограничивают. (Под "хорошей" подрезкой понимается метод, обеспечивающий высокое качество игры при данном объеме вычислительных затрат.)

Тот факт, что просматривается только часть дерева, означает, что процесс обследования должен заканчиваться в вершинах, которые не являются листьями. Это терминальные вершины, или листья, обследуемого поддерева, но не полного дерева. Методы, используемые в программах, основаны на числовой оценке для каждой такой вершины относительной силы обоих игроков в момент достижения данной конфигурации. Эта оценка принимается равной нулю, когда силы партнеров равны, она положительна, когда машина, по-видимому, имеет преимущество, и отрицательна, когда противник машины оказывается сильнее. Эту численную оценку называют оценивающим полиномом (так как обычно она имеет полиномиальный вид, или, проще говоря, вид взвешенной суммы), или статической оценочной функцией ("статической" в том смысле, что оценка производится без дальнейшего обследования дерева).

Статические оценочные функции использовались игроками в шахматы еще задолго до появления электронных "шахматистов". В тех случаях, когда игра в шахматы прерывалась и продолжение ее исключалось (если вспомнить о романтической традиции шахмат, то это могло случаться, например, когда враг подходил к воротам города или когда оба игрока должны были следовать на виселицу), такие статические оценки использовались для определения, кто выиграл.

Важной компонентой любой статической оценивающей функции является материальное соотношение, или перевес фигур. Этот член просто соответствует сравнению фигур, имеющихся у игроков, причем каждой фигуре придается определенное значение ценности. Королям нет смысла придавать какое-то значение ценности, так как уже сам факт, что игра еще не кончилась, означает, что оба короля находятся на шахматной доске. Самое высокое значение ценности имеет ферзь, затем (как существенно менее ценные) следуют в порядке убывания ценности конь, слон и ладья, а наименее ценной из всех фигур является пешка.

Второй важной компонентой оценочной функции, вероятнее всего, должна быть некая мера относительной подвижности фигур, причем более сильным считается тот игрок, у которого подвижность фигур больше. Простым критерием подвижности является число допустимых ходов, имеющихся у игрока. Можно также дать численную оценку контроля центра и других критериев, знакомых игрокам в шахматы.

После того как произведена оценка каждой терминальной вершины обследуемого поддерева, следующий шаг состоит в перенесении результатов этих оценок вверх по дереву ("вверх" означает в направлении корня дерева). Метод, которым это достигается, называется минимаксным; он заключается в следующем. Для альфа-вершин (представляющих позиции, в которых ход делает машина) принимается значение, равное наибольшему значению из указанных для дочерних вершин. Это абсолютно оправдано, поскольку в таком случае машина сделает наиболее выгодный для себя ход. Однако для бета-вершин принимается наименьшее из значений оценки для дочерних вершин, поскольку можно предположить, что противник сделает ход, наименее выгодный машине.

В конечном итоге некоторое оценочное значение приписывается корневой вершине. Поскольку она является альфа-вершиной, это значение будет наибольшим среди значений для дочерних вершин. Ход, который выбирает машина, преобразует существующую на шахматной доске конфигурацию, представленную корневой вершиной, в конфигурацию, представленную той дочерней вершиной, из которой было взято значение оценки для корневой вершины.

Эту процедуру можно рассматривать как эвристическое правило выбора хода в шахматах. Она отличается от других упомянутых нами эвристик тем, что применяется к плохо определенной задаче. Рассматриваемая задача, безусловно, является плохо определенной, поскольку невозможен просмотр всего дерева. И даже если бы полный исчерпывающий просмотр дерева был возможен, эта процедура не обязательно указывала бы совершенный ход, обеспечивающий победу. Тот ход, который человек-шахматист рассматривал бы как наилучший, по-видимому, зависел бы от игровых возможностей и других характеристик противника. Любой выбор, учитывающий подобные обстоятельства, несомненно, представляет собой решение плохо определенной задачи. Описанный же выше машинный метод ни в какой мере не учитывает характеристики партнера по игре.

Действие рассмотренного нами метода было бы очень простым, если бы дерево отсекалось столь сильно, что остались бы только корневая вершина и ее дочерние вершины. Тогда статическая оценочная функция (с. о. ф.) применялась бы к каждой дочерней вершине, и та, что соответствовала бы наибольшему значению функции, определяла следующий ход. Было обнаружено, что у программы, работающей таким образом, очень легко выиграть. Пока еще не удалось найти форму с. о. ф., которая могла бы быть достаточно эффективной. Чем на большее число шагов происходит просмотр вперед, тем лучше игра и тем в меньшей степени качество игры зависит от точного вида с. о. ф.

Рассмотрим простой пример применения с. о. ф. в качестве метода ведения игры в игре в крестики нолики (в США ее называют "тик-так-ту"). Использование просмотра вперед и с. о. ф. в этой игре довольно бессмысленно (его можно рассматривать лишь как иллюстрацию), поскольку существуют другие, более простые алгоритмы беспроигрышной игры. Нильсон, однако, показал, что в программе игры в крестики - нолики может быть использована с. о. ф., вычисляемая следующим образом. Предположим, что машина ставит X, а ее противник - О.

Если конфигурация, которую предстоит оценить, содержит три X подряд (машина выигрывает), то с. о. ф. принимает наибольшее значение, скажем равное + 10. Если подряд стоят три О, то с. о. ф. принимает наименьшее значение, скажем - 10. (Ситуации, в которых имеются выигрышные последовательности обоих типов, следует обойти, делая проверки на всех уровнях дерева на выигрыш и отмечая каждую выигрышную вершину как терминальную.) Для конфигураций, которые не являются выигрышными ни для одного из игроков, с. о. ф. вычисляется следующим образом:

Число строк, столбцов и диагоналей из восьми возможных, все еще открытых для машины, т. е. не заблокированных символом О минус число строк, столбцов и диагоналей, все еще открытых для противника, т. е. не заблокированных символом X.

Как видно из рис. 7, использование такой с. о. ф. не годится, если дерево имеет единичную глубину, т. е. состоит только из корневой вершины и ее дочерних вершин. Для каждого из пяти возможных ходов с. о. ф. оказывается равной нулю. Этот метод не позволяет обнаружить, что следует сделать ход в нижнем левом углу.

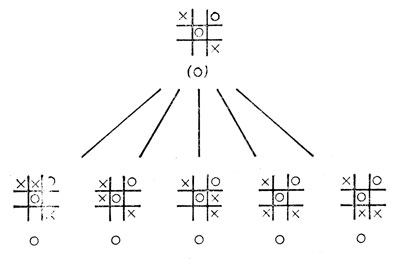
Рис. 7. Неудачная попытка выбрать ход в игре в крестика - нолики с применением статической оценочной функции при единичной глубине дерева

Рис. 8, однако, показывает, что просмотр вперед на один шаг дальше гарантирует выбор хорошего хода. Под каждой конфигурацией на этих рисунках указано некоторое значение. Значения, не заключенные в скобках, получаются в результате статической оценки, а те, что заключены в скобки, соответствуют величинам, полученным в результате применения рассмотренной нами минимаксной процедуры.

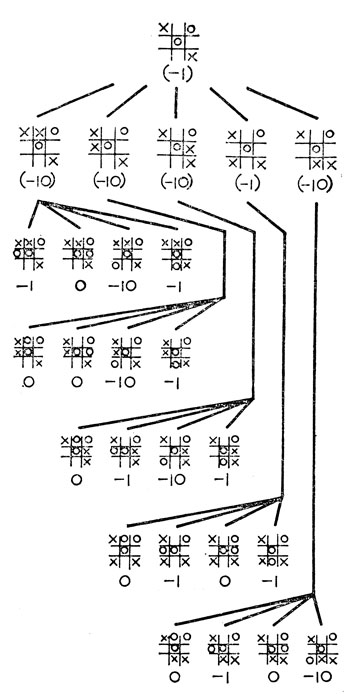
Рис. 8. Выбор хода в игре в крестики - нолики с применением статической оценочной функции при глубине дерева, равной двум

Прямое усечение дерева

Деревья, изображенные на рис. 7 и 8, подрезаны путем отсечения их на определенной глубине. Установлено, что можно достигнуть большего (в смысле качества игры), если использовать другие методы усечения деревьев. Некоторые из методов усечения получили общее название прямого усечения дерева, поскольку решение здесь принимается в процессе работы в прямом направлении от корневой вершины.

В одном из методов прямого усечения дерева выделяются те позиции, которые называют мертвыми, или спокойными, тогда как другие позиции определяют как живые, или беспокойные. Вершина с большей вероятностью может стать терминальной, если представляемая ею конфигурация классифицируется как мертвая. Классификация же позиций на живые и мертвые осуществляется с помощью эвристических правил, причем основная идея состоит в том, что позиция считается живой, если ожидается существенное изменение ее, в частности если существует угроза взятия фигур. (Мы возвращаемся здесь к терминологии игры в шахматы или шашки.)

Другим приемом усечения является выбор перспективного хода. Совершенно очевидно, что дерево разрастается очень быстро, если в нем представляются все из примерно тридцати допустимых ходов (т. е. если фактор ветвления равен примерно 30). Человек сразу же отвергает многие из этих ходов как бесполезные. Если удается уменьшить фактор ветвления путем ограничения числа ходов, рассматриваемых в каждой конфигурации, то рост дерева заметно уменьшается. При заданных вычислительных возможностях это позволяет вести поиск на несколько большую глубину. Важно, однако, выбирать такие ходы, которые в определенном смысле выглядят наиболее обещающими; поэтому в программах игры в шахматы значительное внимание уделяется генераторам перспективных ходов.

Простой генератор перспективных ходов может быть организован так, чтобы для всех тридцати (или примерно тридцати) ходов производилась оценка результирующих конфигураций с использованием статической оценочной функции, а число ходов, представляемых на дереве, было бы ограничено некоторым фиксированным числом (скажем, числом 7). Эти ходы выбираются как наиболее значащие для альфа-вершины или как наименее значащие для бета-вершины.

Обратное усечение дерева

При использовании прямого усечения дерева любым из указанных методов невозможно быть абсолютно уверенным, что результат поиска окажется таким же, каким он был бы, если бы дерево не подвергалось подрезке. В отличие от этого существует метод подрезания дерева (иногда называемый обратным усечением), при котором результат поиска остается неизменным. Метод обратного усечения чаще называют процедурой альфа-бета; такое название обусловлено тем, что для объяснения этого метода приходится обращаться как к вершинам типа альфа, так и к вершинам типа бета.

Поиск по дереву - в том виде, как мы его здесь излагаем, - включает два этапа: построение дерева возможностей с последующим приписыванием его терминальным вершинам числовых значений, определяемых с помощью статической оценочной функции, а затем применение минимаксной процедуры для передачи значений вверх по дереву. В процедуре альфа-бета требуется, чтобы эти два этапа были объединены, так чтобы значения связывались с вершинами по мере формирования дерева. В силу особенностей минимаксной процедуры в таком случае удается избежать построения целых кусков дерева, что иногда уменьшает время вычисления на несколько порядков.

Наиболее естественно представить рост дерева в виде ярусов, отходящих от корневой вершины: сначала формируются все дочерние вершины для корня, затем все внучатые и т. д. Построение дерева таким образом называется поиском в ширину. Чтобы воспользоваться преимуществами процедуры альфа-бета, дерево следует строить иначе - методом поиска в глубину. При этом выбор новой вершины на каждом шаге построения производится таким образом, чтобы эта новая вершина была дочерней для вершины, построенной самой последней.

Чтобы пояснить, как это делается, рассмотрим дерево, изображенное на рис. 8; на рис. 9 оно перерисовано таким образом, что вершины (исключая корневую) пронумерованы в том порядке, в каком они строились бы в процессе поиска в ширину. (Строго говоря, это один из возможных порядков, поскольку порядок построения дочерних вершин для любой данной вершины совершенно произволен.)

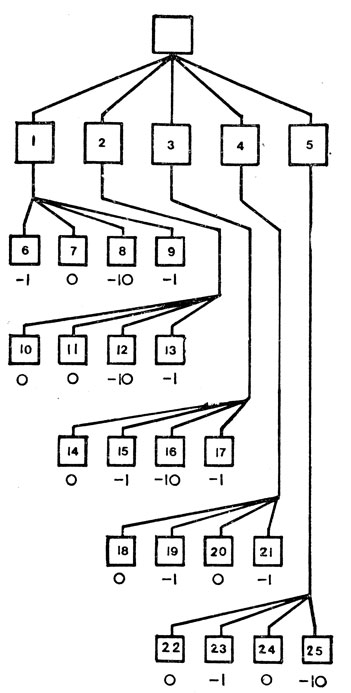
Рис. 9. Дерево, изображенное на рис. 8, с вершинами, занумерованными в порядке их построения при поиске в глубину

При поиске в глубину - при том же самом порядке построения дочерних вершин для данной вершины - первой новой вершиной будет вершина с номером 1. Однако следующей будет не вершина 2, а дочерняя вершина для самой последней из построенных вершин, т. е. вершина 6. Казалось бы, что следующей должна быть дочерняя вершина для вершины 6, но этого быть не может, поскольку вершина с номером 6 удовлетворяет терминальному условию остановки. Другие дочерние вершины для вершины 1, а именно вершины с номерами 7, 8 и 9, строятся прежде, чем происходит возвращение к прерванной генерации дочерних вершин корневой вершины (и если вершина 7 не удовлетворяет терминальному условию, то под ней должно быть построено все поддерево, прежде чем начнет строиться вершина 8).

Чтобы сэкономить объем поиска при применении процедуры альфа-бета, необходимо производить оценку каждой терминальной вершины, как только она будет построена. Оценка для нетерминальной вершины находится лишь после того, как будут оценены все ее дочерние вершины. Но как только будет оценена одна из таких дочерних вершин, с родительской вершиной можно связать предположительное возвращаемое значение (п. в. з.). Если родительская вершина при этом является альфа-вершиной, то п. в. з. равно наибольшей из полученных до сего момента оценок для дочерних вершин. Если же родительская вершина является бета-вершиной, то ее п. в. з. равно наименьшей из оценок, полученных для дочерних вершин. Как только п. в. з. приписано некоторой альфа-вершине, при дальнейшем построении дерева это значение может лишь возрасти по величине. Если же п. в. з. оказывается приписанным некоторой бета-вершине, то впоследствии это значение может только уменьшаться.

Два последних правила дают возможность в процессе построения дерева или поиске в глубину понять, что некоторые из еще не построенных вершин никак не могут повлиять на конечный результат. Тогда обратное усечение равносильно просто отказу от построения таких вершин. Если это не те вершины, которые стали бы терминальными, то идущие под ними поддеревья отсекались бы весьма эффективным образом, что позволило бы существенно сэкономить вычислительные затраты,

Оценивая дерево, показанное на рис. 9, с учетом этих соображений, следовало бы сформировать и оценить вершины 6, 7, 8 и 9 для того, чтобы оценить вершину 1, придав ей значение -10, которое затем становится также п. в. з. для корневой вершины. После этого строится вершина 2, а за ней - вершины 10, 11 и 12. После оценки вершины 12 п. в. з. для вершины 2 равно -10, т. е. равно п. в. з. для корневой вершины. Теперь ясно, что значение вершины 2 будет равно -10 или меньше, поскольку она является бета-вершиной и ее п. в. з. может только уменьшаться. Значение вершины 2, следовательно, не может повлиять на значение корневой вершцны (так как последняя является альфа-вершиной и ее значение не может стать меньше того, что имеется на данный момент, т. е. меньше -10). Поэтому нет смысла строить поддерево ниже вершины 2 - следовательно, вершина 13 формироваться не будет.

Итак, общее правило, вероятно, заключается в том, что если п. в. з. для бета-вершины становится меньше или равным п. в. з. для ее родительской альфа-вершины, то нет необходимости строить дальше поддерево, идущее от такой бета-вершины. Если так случается, то в процессе поиска мы сталкиваемся с альфа-отсечением.

Выполняется также дополнительное правило, которое обеспечивает экономию в случае бета-отсечения: если п. в. з. для какой-то альфа-вершины становится больше или равным п. в. з. для ее родительской бета-вершины, то нет смысла строить дальше поддерево, идущее ниже такой альфа-вершины.

В рассматриваемом примере после отказа от построения вершины 13 в процессе поиска будут формироваться вершины 3, затем 14, 15 и 16, после чего другое альфа-отсечение позволяет отказаться от построения вершины 17, Далее формируются вершина 4 и все ее дочерние вершины: 18, 19, 20 и 21. Значение для вершины 4 равно -1, и п. в. з. для корневой вершины возрастет до этой величины. Затем строится вершина 5, за которой следуют вершины 22 и 23. Для вершины 5 п. в. з будет равно -1, т. е. оно равно п. в. з. для корневой вершины. Поэтому альфа-отсечение сделает излишним построение вершин 24 и 25.

Рассматривая дерево большей глубины, мы могли бы продемонстрировать экономию, связанную с бета-отсечением. В настоящем примере экономия от обратного отсечения невелика: просто не пришлось оценивать вершины 13, 17, 24 и 25. Следует помнить, что эти вершины не обязательно должны быть терминальными и что идущие под ними поддеревья при другом исходном дереве также были бы отсечены.

Экономия зависит от порядка, в котором строятся дочерние вершины каждой конкретной вершины. Если бы порядок соответствовал приоритету слева направо, как показано на рис. 10, то экономия была бы значительно больше. В этом случае отпала бы необходимость в построении вершин 6, 7, 9, 10, 11, 14, 15, 17, 22, 23 и 24.

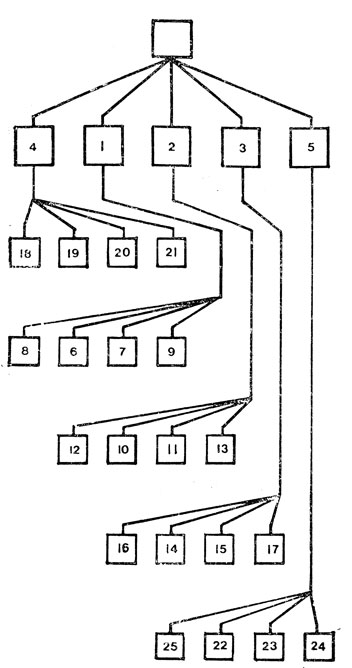
Рис. 10. То же дерево, но с вершинами, переупорядоченными таким образом, чтобы извлечь максимум из процедуры альфа-бета

Чтобы извлечь максимум выгоды из процедуры альфа-бета, целесообразно использовать для упорядочивания процесса построения вершин эвристические методы. Полезной эвристикой, в частности, является использование статической оценочной функции (с. о. ф.) для упорядочивания дочерних вершин какой-либо конкретной вершины, при котором приоритет отдается наивысшим значениям с. о. ф. для дочерних вершин в случае альфа-вершины и наинизшим значениям с. о. ф. для дочерних вершин в случае бета-вершины. Развитию эффективных стратегий, использующих эвристическое упорядочение в процедуре альфа-бета, уделяется большое внимание; здесь разработаны стратегии, гораздо более сильные, чем та, которую мы описали (см. [1]).

Другие методы игры в шахматы

Эффективность шахматных программ постоянно возрастает, и в настоящее время достигнут весьма высокий класс игры. Ныне существуют программы, которые бросают вызов мастерам шахмат и которые обычно легко побеждают в поединке с шахматистом-дилетантом. Тем не менее эти программы работают описанным нами методом "грубой силы", который основан на построении и исследовании дерева возможностей.

Вполне очевидно, что подобный способ выбора хода не соответствует тому, как поступает в этом случае человек. Шахматисты, безусловно, не думают о крупномасштабном поиске: они предпринимают весьма ограниченный поиск, рассуждая примерно так: "Если я пойду туда, он ответит..., если же я пойду туда, моя фигура окажется незащищенной..." При этом учитывается лишь небольшое число возможностей. Говорят, что один шахматный мастер на вопрос, как много ходов он рассмотрел, прежде чем сделать выбор, ответил: "Ровно один, но верный".

О том, что процесс принятия решения, который осуществляет шахматист, не похож на процесс, используемый в шахматных программах, свидетельствует тот факт, что шахматисты могут говорить друг с другом о шахматах и с интересом и пользой для себя изучают литературу по шахматам. Обсуждая проблемы шахматной игры, они говорят не о поиске по весьма большому дереву возможностей, а прибегают часто к таким эмоциональным понятиям, как атака, защита или угроза. Воплотить же подобные критерии в программе для вычислительной машины нелегко. Однако некоторые исследователи, работающие в области машинной игры в шахматы, предполагают, что дальнейшего прогресса здесь, по-видимому, можно достигнуть, изучая методы игры шахматистов.

Многократный чемпион мира М. М. Ботвинник в течение ряда лет отстаивает точку зрения, что в машинных шахматах возможно использовать методы, подобные тем, которыми вооружен человек-шахматист. В одном из недавних выступлений Ботвинник рассказал о своих методах, также основанных на анализе дерева возможностей, но имеющего фактор ветвления, лишь немного превосходящий единицу. Другими словами, Ботвинник утверждает, что располагает множеством эвристик, которые обычно указывают на единственный "следующий ход"^*.

^* (См. Предисловие редактора перевода. - Прим. ред.)

Мичи [4] также указал такой подход к машинным шахматам, который, несомненно, в большей степени соответствует методам, используемым шахматистом-человеком. В настоящее время этот автор особое внимание уделяет анализу шахматных окончаний, где ситуация упрощается из-за наличия небольшого числа фигур. Когда число игровых ситуаций становится достаточно малым (соответственно числу оставшихся фигур), число их различных классов оказывается вполне обозримым. Для каждого такого класса перечисляются "вопросы", относящиеся к конфигурации фигур на шахматной доске. Такие вопросы легко формулируются на обычном языке, но на них легко "отвечает" и программа. Это вопросы типа: "Находятся ли такие-то фигуры на одной линии (одной вертикали или одной диагонали)?", "Находится ли такая-то фигура в безопасности?" Ответы связываются с указанием относительно хода посредством таблицы подобно тому, как используется эвристическая таблица в универсальном решателе задач. Хотя Мичи не ограничивается столь простыми шахматными окончаниями, как Торрес и Кьюведо, его подход в настоящий момент имеет весьма ограниченное применение.

Различные исследователи, работающие в области искусственного интеллекта, в том числе Эшби [5], неоднократно указывали на шахматы как на характерный пример, полезный для исследования мыслительных процессов человека. Трудность имитации методов человеческого мышления подтверждает точку зрения, что в этом процессе заложено что-то весьма глубокое и малодоступное нашему пониманию. Другие исследователи, однако, отрицали, что шахматы можно считать в этом отношении наиболее характерной задачей, поскольку она не настолько типична для повседневной деятельности человека. Шахматы требуют методов мышления, которые отличаются от методов, используемых в реальной жизни, точно так же, как теория чисел отличается от использования чисел на практике. (В теории чисел большое внимание уделяется точной делимости; поэтому, например, простое число 23 считается существенно отличным от соседнего числа 24, которое можно представить в виде произведения других чисел.)

Отчасти именно поэтому в последние годы уделяется меньше внимания машинным шахматам как средству выяснения природы интеллекта вообще, хотя сама по себе работа в этой области продолжается. Если исследования, касающиеся моделирования человеческих методов ведения игры, принесут свои плоды, то машинные шахматы, возможно, еще сыграют роль своего рода "переднего эшелона", как предсказывали Эшби и другие ученые, - по крайней мере в рамках определенного подхода к выяснению природы человеческого интеллекта.