6. Другие игры

Шахматы отнюдь не единственная игра, которой уделялось внимание при работе над проблемой искусственного интеллекта. Предметом исследования стали многие известные и малоизвестные игры: предполагалось, что их изучение либо позволит поставить задачи соответствующего уровня сложности, либо поможет уяснить некоторые специфические особенности игры.

Многие из исследованных игр оказались гораздо проще шахмат. И это неудивительно, поскольку большинство игр в самом деле много проще шахмат. Однако существует так называемая игра го, которая считается более трудной, чем шахматы, как для людей, так и для вычислительных машин. Как и шахматы, это очень древняя игра: она известна на Востоке уже около четырех тысяч лет и до сих пор является одной из популярнейших игр в Японии.

Шашки

Среди работ, посвященных моделированию с помощью ЭВМ игр, отличных от шахмат, наиболее известна программа Сэмюэля [1] для игры в шашки. Эта игра значительно проще шахмат^*. Согласно оценкам Шеннона, число возможных игровых ситуаций в шашках примерно равно кубическому корню из числа возможных ситуаций в шахматах. (Для шахмат, по подсчетам Шеннона, это число составляет 10⁴³. Эту оценку оспаривает Гуд, который считает, что она, по-видимому, верна с точностью до одной тысячи, хотя многие из позиций весьма маловероятны. По мнению Гуда, число возможных игровых позиций в шахматах, вероятность которых не является исчезающе малой, составляет 10²⁴.)

^* (Имеются в виду шашки для доски 8×8. - Прим. ред.)

Основная цель работы Сэмюэля по машинному ведению игры в шашки заключалась отнюдь не в игре как таковой. Он намеревался исследовать возможности включения в программы для вычислительных машин "способности к их совершенствованию" на основе накопленного опыта, или, другими словами, способности к "приобретению навыка". Сэмюэль считал, что шашки более подходят для подобного исследования, чем шахматы, так как ввиду несложности самой игры возникает меньше препятствий для решения исходной проблемы.

В общих чертах метод, использованный Самюэлем для игры в шашки, мало отличался от наиболее распространенного подхода к машинной игре в шахматы, т. е. также опирался на изучение дерева возможностей. Сэмюэлю удалось реализовать две формы обучения: накопление и обобщение.

Из этих двух форм накопление^* менее интересно и менее эффективно. Оно сводится к хранению в памяти вычислительной машины большого числа конфигураций на шашечной доске из числа тех, что возникают в ходе игры. Это конфигурации, которые реально имели место и, следовательно, были представлены в корневой вершине дерева (в отличие от гипотетических конфигураций, представленных в остальных частях дерева).

^* (От англ. root learning; смысл этого понятия будет ясен из дальнейшего. - Прим. перев.)

Вместе с каждой конфигурацией в памяти хранилась также ее числовая оценка, которая получилась путем построения дерева, применения с. о. ф. к терминальным вершинам и передачи значений вверх по дереву посредством минимаксной процедуры. Такая оценка в общем случае отличается от оценки, полученной путем непосредственного применения с. о. ф., и оказывается более полезной при определении хода в игре.

Имея в памяти некоторое множество конфигураций вместе с их оценками, программа в процессе работы ищет соответствие между конфигурацией, отвечающей каждой из вершин дерева, и конфигурациями из числа запомненных. Если такое соответствие установлено, то хранимая в памяти оценка передается в эту вершину - в результате отпадает необходимость строить какое-либо поддерево, которое могло бы возникнуть под этой вершиной.

Несомненным преимуществом накопления следует считать экономию времени, поскольку накопление позволяет избежать построения некоторых поддеревьев. Это еще одна форма прямого усечения дерева. Существует, однако, определенная связь между временем вычисления и качеством игры, поскольку размер дерева ограничивается отпущенным временем. Таким образом, накопление либо обеспечивает экономию времени, либо позволяет достичь лучшего качества игры за то же время путем использования несколько большего дерева.

Отметим еще одно обстоятельство, благодаря которому использование накопления улучшает качество игры. Когда находится соответствие между какой-либо вершиной и конфигурацией из списка хранимых в памяти, в вершину переносится оценка, сформированная тогда, когда данная конфигурация находилась в корневой вершине и под ней имелось целиком все дерево возможностей. Следовательно, эта оценка основывается на большем дереве, чем то, которое было бы сформировано под указанной вершиной, если бы такого соответствия не обнаружилось. И хотя с точки зрения вычислительных затрат накопление и представляет собой форму усечения, оно влияет на результат поиска так, словно ветви дерева там, где накопление использовалось, оказываются длиннее, чем они были бы в отсутствие накопления.

Безусловно, размер списка конфигураций, который может храниться в памяти и использоваться, ограничен сверху. Не все конфигурации, встречающиеся в игре, могут храниться в памяти, и нужно, чтобы этот список не был перегружен конфигурациями, которые вряд ли когда встретятся. Сэмюэль достигает этого тем, что для каждого элемента списка ведется подсчет числа ходов, сделанных с момента, когда этот элемент был последний раз использован. Если с момента последнего употребления какого-то элемента прошло много ходов, то он вычеркивается из списка и на его место ставится другой, взятый из текущей игры. Благодаря этому список содержит конфигурации, которые достаточно часто встречаются в ходе игры.

Сэмюэль установил, что в шашках накопление весьма полезно, но, по общему убеждению, в шахматных программах дело обстоит иначе'. Большее число возможных конфигураций означает, что необходим более длинный список (чтобы он оказался полезным), но возникающее при этом увеличение вычислительных затрат делает его, по существу, бесполезным.

Другая форма обучения, использованная Сэмюэлем, - обобщение. Оно позволяет программе в ходе игры улучшать свою с. о. ф.

Обычно с. о. ф. представляет собой полином; в простейшем виде это полином первой степени, или взвешенная сумма, скажем s, которая вычисляется следующим образом:

где а₁, а₂ и т. д. - величины различных вычисляемых критериев, таких, как материальное соотношение, подвижность, контроль центра и пр. Они взвешиваются по отношению друг к другу с помощью коэффициентов k₁, k₂, ... . Полином может быть также и более высокой степени относительно переменных а, например

но для иллюстрации метода достаточно рассмотреть случай полинома первой степени.

Качество игры зависит от подходящего выбора величин коэффициентов k₁, k₂, ..., и обобщение является средством их подгонки, обеспечивающей улучшение игры. Метод обобщения представляет собой пример оптимизации с использованием процедуры, часто называемой подъемом на гору. Имеется начальный набор значений k₁, k₂, ..., и в каждый момент времени эти коэффициенты определяют рабочую точку. Рабочая точка перемещается в пределах многомерного пространства по мере подгонки величин k в поисках положения, в котором оптимизируется определенная реакция, или целевая функция. Термин "подъем на гору" взят здесь потому, что альпинист аналогичным образом изменяет свое положение в двух измерениях (по широте и по долготе), чтобы максимизировать свою высоту.

Чтобы воспользоваться методом подъема на гору, следовало бы дать программе возможность сыграть некоторое количество игр с определенным партнером, выбрав какое-то начальное множество коэффициентов k_i, а затем сыграть еще некоторое количество игр, сделав пробное изменение в положении рабочей точки. Таким пробным изменением могло бы быть незначительное увеличение значения k_i. Если программа во втором множестве игр выигрывает чаще, чем в первом, то принимается новое значение k_i; в противном случае происходит возвращение к старой величине и производится какое-то другое пробное изменение.

Очевидно, что при любом методе, зависящем от результатов всей игры в целом, надо двигаться очень и очень медленно. Поскольку партнер, по всей видимости, не может играть абсолютно ровно, необходимо, чтобы два указанных множества игр были большими, однако при этом возникают свои трудности. Было бы лучше найти средство для подбора величин k_i в ходе ведения игры. И Сэмюэль придумал, как это сделать.

Предложенный им способ основан на том, что качество игры программы растет с глубиной просмотра возможностей. Кроме того, работа программы с ростом глубины просмотра все в меньшей степени зависит от точного вида с. о. ф. Таким образом, оценка конфигурации, получаемая в результате передачи оценок вверх по дереву возможностей, в некотором смысле оказывается "лучше", чем оценка, получаемая в результате прямого применения с. о. ф.

Если может быть найдено средство вычисления с. о. ф., обеспечивающее четкое совпадение между переданным назад по дереву значением для каждой конфигурации и результатом прямого применения с. о. ф. к той же самой конфигурации, то такая оценка должна быть равнозначна изучению всего полностью построенного дерева игры. В методе обобщения осуществляется подбор таких коэффициентов k_i, которые улучшают соответствие между результатом прямого применения с. о. ф. и результатом использования той же самой с. о. ф., переданным вверх по дереву возможностей.

Если s - результат прямой оценки с помощью с. о. ф., a s_b - результат передачи оценки по дереву, то можно считать их разность ошибкой е, где

Сэмюэль сделал так, что в его программе вычисляется текущая корреляция между е и а₁, а₂ и т. д. Положительная корреляция между е и любым значением a_i указывает, что соответствующий коэффициент k_i следует уменьшить, а отрицательная корреляция означает, что его надо увеличить. Этот принцип, по существу, совпадает с тем, что Дональдсон [2] называет "декорреляцией ошибки".

При применении рассматриваемого метода требуется уделить внимание обеспечению его устойчивости. Нетрудно получить схему, приводящую к бесконечному "рысканию" вокруг оптимума. Окончательный вариант, использованный Сэмюэлем, не дает плавного приближения к оптимуму, свойственного процедуре подъема на гору. В нем после каждого хода производится весьма существенное изменение величин коэффициентов k_i.

Несмотря на сказанное о преимуществах, которые ожидаются от хорошего согласования прямого применения с. о. ф. с переданными назад по дереву величинами, из такого согласования не обязательно вытекает хорошая игра. Идеальное согласие наблюдалось бы и в случае, если все k_i положить равными нулю. Но это, очевидно, никак не могло привести к хорошей игре. На самом деле при любом множестве k_i, обеспечивающем хорошее качество игры, можно обратить все знаки k_i и получить очень слабую игру (фактически игру в "поддавки"). Однако согласие между двумя типами оценок при этом будет столь же хорошим, как и для первоначальных значений k_i.

Сэмюэль понимал, что его метод позволяет прийти к состояниям, которые обеспечивают хорошее согласие, но слабую игру. Чтобы избежать такой ситуации, коэффициент при одном из членов с. о. ф. был зафиксирован и приравнен некоторой положительной величине (скажем, единице), тогда как другие коэффициенты изменялись. Выделенный член был связан с оценкой материального соотношения, поскольку разумно предполагать, что игроку всегда выгодно, чтобы его шашки на доске сохранялись.

(Следует отметить, что указанное может служить иллюстрацией к замечанию, сделанному Селфриджем по отношению к проблеме искусственного интеллекта вообще. Люди подходят к решению таких задач, как шахматные, исходя из своего жизненного опыта и навыков, приобретенных за многие годы жизни. Едва ли стоит убеждать человека, что он должен стараться сохранять свои фигуры и захватывать фигуры противника - эту мысль он усвоил еще в детстве, когда спорил с товарищами из-за игрушек. Однако машине это необходимо "сказать", сделав положительным коэффициент при члене, обеспечивающем преимущество в фигурах.)

Установив коэффициент при материальном соотношении равным единице, мы получим следующее выражение для с. о. ф.:

Обобщение основано на подгонке численных параметров. Процедуру подгонки можно использовать для выбора тех членов, которые должны быть включены в с. о. ф. Сэмюэль держал в своей программе больший "ассортимент" критериев (а₁, а₂, ... и т. д.), чем тот, что допускался для использования в конкретной с. о. ф. в каждый момент времени. Используемое множество критериев видоизменялось самым непосредственным образом: если какое-то из значений k_i оставалось близким к нулю в течение достаточно длительного времени, то тот член с. о. ф., к которому относится этот коэффициент, изымался из рабочего множества, а на его место ставился другой - из числа ожидающих своей очереди. Изъятый член добавлялся к множеству ожидающих и мог быть заново внесен в с. о. ф. позже, при другой замене.

Возможность изменения множества членов с. о. ф. придает данному методу обучения новый характер. Теперь его можно воспринимать как некую самоорганизующуюся систему. Если же действие сводится только лишь к подгонке параметров, то этот термин, по-видимому, неприложим. Здесь уместнее более "слабый" термин - самооптимизация. Между этими понятиями нельзя провести четкую границу, поскольку, по существу, нет четкого различия между образованием новой связи (структурное изменение) и включением усиления, благодаря которому из нуля делается конечная величина (изменение параметра). Различие, однако, состоит в том, насколько легче описать систему одним из способов, чем другим.

Сэмюэль показал, насколько эффективен метод обучения через обобщение. Он организовал работу программы таким образом, что она могла вести игру непрерывно днем и ночью, причем имитировала одновременно двух игроков: альфа и бета (эти наименования никак не связаны с использованными ранее аналогичными обозначениями типов вершин). Игроку альфа разрешалось модифицировать его с. о. ф. путем обобщения, тогда как игрок бета пользовался фиксированной с. о. ф. Когда альфа выигрывал игру, игрок бета копировал с. о. ф., которую имел игрок альфа. С другой стороны, если игрок бета выигрывал подряд три игры, то его с. о. ф. копировалась игроком альфа. Это гарантировало возможность возвращения игрока альфа к прежнему положению в том случае, если процесс подгонки параметров происходил в нежелательном направлении.

Хотя две формы обучения, предложенные Сэмюэлем, оказываются достаточно эффективными, они, безусловно, сильно уступают возможностям человека. И с. о. ф., даже модифицированная посредством обобщения, все равно остается лишь комбинацией критериев, разработанных и запрограммированных Сэмюэлем. Этот недостаток трудно сформулировать в точных терминах и понятиях. Он связан с тем, что в некотором отношении новые варианты с. о. ф. отнюдь не являются качественно, новыми. Сам Сэмюэль хорошо понимал этот их недостаток и много размышлял над ним. Этот вопрос мы обсудим более подробно в конце настоящей главы.

Описанные методы обучения обладают еще одним недостатком: заложенная в них программа не способна "усваивать" силу или манеру игры своего противника и реагировать на нее (если это и происходит, то лишь весьма опосредованно, так как поведение партнера определенным образом влияет на выбор конфигураций на доске, которые реально имели место). Рассмотренные методы не предусматривают также возможности обучения путем копирования игры противника. Исследования, направленные на создание более глубоких методов обучения, были осуществлены на примере других настольных игр.

Игры типа "крестики - нолики"

Мы уже говорили о такой хорошо знакомой нам с детства игре, как крестики - нолики. Эта игра не представляет большой трудности и для вычислительной машины. Вместе с тем она представляет собой простейший вариант целого класса игр, которые разыгрываются на поле, разбитом на клетки, причем два (или более) игрока помещают элементы соответствующего типа в незанятые клетки.

Игру крестики - нолики можно вести на трехмерной решетке вместо обычной двумерной. Длина каждой строки символов в таком случае обычно принимается равной четырем. Можно играть также в четырех и более измерениях, написав специальную программу для вычислительной машины, обыграть которую людям очень трудно: дело в том, что люди не в состоянии зрительно представить пространство с размерностью более трех.

Существует двумерная игра типа "крестики - нолики", но совершенно другого уровня трудности; она известна под разными названиями: пеггити, гоу-мок или пять в ряд. Доска обычно имеет 19×19 клеток (хотя это несущественно), и задача каждого игрока состоит в том, чтобы первым расположить пять принадлежащих ему элементов одного типа в одну линию, которая может проходить горизонтально, вертикально либо по диагонали. Игроки ходят по очереди, помещая каждый раз один из своих элементов в свободные клетки поля.

Объединять в одну три разные игры с разными названиями вряд ли разумно - ведь, несмотря на их сходство, каждая из игр имеет свои особенности. Так, согласно Муррею и Элкоку [3], в игре гоу-мок к выигрышу предъявляется требование, чтобы в одном ряду было пять и только пять элементов одного типа - ряд из шести не годится. Для пеггити и пять в ряд требование обычно состоит в том, чтобы расположить пять элементов в одну линию, даже если эти пять элементов составляют часть какой-то линии большей длины. На практике, как установил Квинтон, это различие несущественно. При изучении очень большого числа игр, сыгранных по правилам пеггити, было обнаружено, что цепочки, включающие более пяти элементов, никогда не образовывались. В основном игры велись между людьми и программой для вычислительной машины, однако в ряде игр партнерами были люди. (Тот факт, что на практике не образовывалось цепочек из шести и более элементов, не доказывает, что возможность их образования не влияет на ход игры. Однако анализ игр, проведенный игроками, приводит к иному заключению.)

Для игр рассматриваемого типа нет необходимости в обследовании дерева возможностей. Поскольку после размещения элементы остаются на своих местах, за построением выигрывающей комбинации можно следить непосредственно по ним.

Для этих игр можно найти "непобедимые" комбинации элементов, т. е. такие, которые приводят к выигрышной ситуации. Даже в случае привычной нам формы игры крестики - нолики на решетке 3×3 возможны конфигурации "вилка", которые обеспечивают победу (но которые могут возникнуть лишь в играх с очень малоопытным партнером). На рис. 11 показаны две конфигурации, в которых игрок "О" построил "вилку", обеспечившую ему победу, несмотря на то что очередной ход за игроком "X".

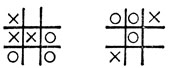
Рис. 11. Ситуации, возможные в игре в крестики - нолики (следующий ход за игроком 'X'). В обоих случаях игрок 'О' сформировал 'вилку', которая гарантирует ему победу

В играх пеггити и гоу-мок возможны различные комбинации, которые позволяют игроку добиться выигрыша; для этого он должен а) построить из своих элементов одно из таких сочетаний и б) не дать противнику построить подобные сочетания из его элементов.

Муррей и Элкок написали программу, которая способна обучаться играть в гоу-мок. В конце игры с неким противником программа анализирует запись ходов и выясняет, какого рода сочетания элементов предшествовали выигрышу. На первых этапах обучения в основном выигрывал партнер, поэтому можно считать, что программа обучалась, копируя партнера. Когда же программа выделяла непобедимые сочетания (выигрышные комбинации), она начинала играть, достигая таких комбинаций для себя и препятствуя их построению у партнера.

В программе Муррея - Элкока сочетания хранятся в обобщенной форме, в которой не делается различия между горизонтальными или вертикальными цепочками и цепочками, расположенными по диагонали. Некоторые такие обобщения являются полезным свойством обучающейся программы. Сочетания элементов равнозначны независимо от того, под какими углами расположены составляющие их цепочки.

Однако в программе, предназначенной для обучения путем использования слабостей партнера, предпочтительней, если есть возможность различать сочетания элементов, содержащие диагональные цепочки, и сочетания, включающие только горизонтальные или только вертикальные цепочки. Установлено, что игроки-люди с большей вероятностью пропускают непобедимые сочетания в том случае, когда те содержат диагональные цепочки, чем в случае, когда такие цепочки в них отсутствуют, и на самом деле "обучающаяся" программа должна строиться с использованием этого обстоятельства.

Игру пеггити изучал Квинтон [4]. Он исследовал процесс приобретения навыка игры людьми, с тем чтобы в дальнейшем использовать подобные методы в обучающейся программе. Он предлагал каждому игроку-человеку сыграть серию игр с программой, написанной для вычислительной машины. В каждой игре эта программа записывала все ходы, а также время, затраченное противником на выбор хода.

Квинтон выбрал для исследования данную конкретную игру потому, что она достаточно трудна и вполне может быть реальным вызовом для игрока, но вместе с тем не настолько трудна, чтобы люди не могли освоить навыки этой игры за сравнительно короткое время эксперимента. Другое преимущество данной игры заключается в том, что в нее играют немногие (по крайней мере за пределами стран Юго-Восточной Азии), поэтому игроки начинают приобретать навыки практически с нуля. Использованная программа могла играть, руководствуясь стратегиями трех уровней. В каждом эксперименте она начинала с самого низкого уровня, переходя на следующий, как только человек выигрывал две партии подряд.

Были составлены программы, позволяющие анализировать записи проведенных игр с целью обнаружить точки, в которых возникали важные сочетания (Квинтон называет их ключами). Впоследствии можно было проследить развитие или блокирование каждого ключа (автоматически, с помощью программы анализа), и тогда возникала возможность выяснить, усвоил ли игрок в этот момент значение ключа данного типа. Обучение с помощью ключа не обязательно должно быть сознательным процессом. Проведенное исследование призвано было способствовать выяснению вопросов обучения в более широком плане. Программу анализа можно было бы непосредственно приспособить для создания играющей программы, способной обучаться извлекать выгоду из слабости и ошибок своего партнера.

Игра го

Исследование дерева возможностей оправдано лишь в том случае, если число возможных ходов из данной позиции не чрезмерно велико. Использование же методики, применимой к играм типа "крестики - нолики", возможно только тогда, когда выигрышные комбинации образуются в некоторой подобласти ограниченного размера. Ни одно из названных условий неприменимо к игре го.

Эту игру (см. [5]) некоторые считают более сложной, чем шахматы. Безусловно, написать программу для вычислительной машины, способной играть в эту игру с какой-нибудь степенью профессиональности, - задача весьма трудная.

Игра го ведется на прямоугольной решетке наподобие игры гоу-мок или пеггити, и игроки размещают фишки по очереди точно таким же образом. Цель игры, однако, состоит не в том, чтобы образовать конкретную комбинацию (типа цепочки из фишек, принадлежащих данному игроку), а в том, чтобы "окружить" и "взять" области, целиком покрытые фишками противника. "Окружать" нужно так, чтобы любой шаг по вертикали или по горизонтали из окруженной области приводил к клетке, занятой одной из фишек окружения. Если же существует возможность сделать шаг в замкнутый пустой "остров", то это сводит "окружение" на нет.

Эта задача, по существу, носит геометрический или топологический характер и обладает тем свойством, что процесс восприятия ее человеком настолько специфичен, что до сих пор его не удалось смоделировать в программе для вычислительной машины. Программы, написанные для игры го, по человеческим стандартам, играют пока весьма слабо.

Случайные игры

Все игры, о которых мы говорили до сих пор, относятся к играм с полной информацией. Иначе говоря, в этих играх ничто (за исключением, разве, мыслей противника) не скрыто от игрока. В них отсутствует случайный элемент такого типа, как при бросании кости, в рулетке или при сдаче колоды карт. С точки зрения теории игр Бореля и фон Неймана (см. книгу Вайды [6]) игры с полной информацией считаются "тривиальными", но поиск эффективных игровых стратегий и в этом случае отнюдь не тривиальная задача.

Вычислительные машины легко запрограммировать для ведения игр со случайным элементом. Программа для игры трик-трак в одном случае на самом деле побила чемпиона мира [7]. Одиночный выигрыш в таких играх не рассматривается как сколько-нибудь значительное событие, и игра вычислительных машин, по мнению специалистов, далека от совершенства.

Даже там, где вычислительная машина не ведет непосредственно игру, но используется для анализа, результаты которого человек хранит в своей памяти, выигрыш от применения машины может быть существенным. Слейгл [8] описывает удивительный случай с профессором Торпом, который занимался играми черный валет и баккара с использованием машинного анализа. Удачная игра принесла ему огромное состояние, и, не имея сил противостоять губительной страсти, профессор в конце концов опустился до того, что стал работать в казино Лас-Вегаса.