Несколько алгоритмов развития

Мы можем теперь спросить: по каким алгоритмам развивается такая сеть? Может ли при этом появиться заданная пространственная структура, если инструкции были даны только одному исходному автомату, и если да, то какими должны быть эти инструкции?

Начнем с исследования самого простого расположения: автоматы расположены по прямой линии. Бесконечный рост по прямой линии может быть осуществлен с помощью таких инструкций:

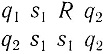
Это происходит так (пишем подряд мгновенные описания):

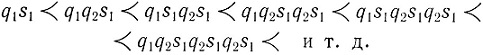
Следующим нашим вопросом, конечно, будет вопрос о том, как ограничить этот рост, т. е. наш автомат должен быть машиной Тьюринга для моделирования развития, а не рака.

В модели Пенроуза степень роста определяется числом "кирпичей" и продолжительностью периода подачи энергии. Подобно вышесказанному, реальный организм нуждается в пище, дающей энергию и строительные материалы. В этом смысле среда оказывает влияние, но оно имеет внешний характер: пища - необходимое, но не достаточное условие роста и развития. И очевидно, что даже, если пищи достаточно, организм со временем останавливает свой рост.

В этой абстрактной модели мы предполагаем, что имеется достаточно энергии и строительного материала, поскольку это не имеет никакого отношения к нашей задаче, и подачу символа s₁ на исходный автомат мы принимаем неограниченной. (Можно остановить рост внешним воздействием, кончив подавать s₁.)

Написать набор инструкций для ограниченного роста труднее, чем для неограниченного, особенно потому, что все автоматы должны иметь идентичные наборы инструкций, так как R было определено для этого случая. Однако в простейшем случае, когда должен возникнуть только один новый автомат, это можно сделать так:

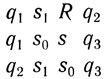
Мгновенные описания таковы:

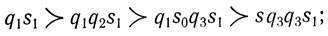
работа окончена.

Аналогично этому следующий набор инструкций дает цепочку из трех автоматов:

Мгновенные описания этого процесса таковы:

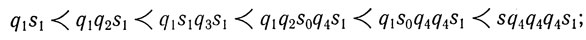
работа окончена.

Для цепочки из четырех автоматов набор инструкций таков:

Мгновенные описания таковы:

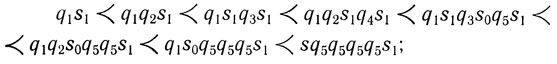
работа окончена.

И для цепочки из пяти автоматов имеем:

Мгновенные описания:

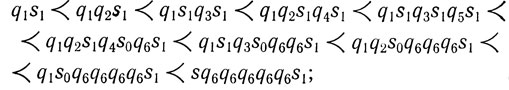
работа окончена.

Это происходит так: каждое s₁, поданное на вход, пройдя цепочку, вызывает воспроизведение, a s₀ переводит автомат сразу в конечное состояние; исключение составляет исходный автомат, который, меняя свои состояния, доходит до намеченного конечного состояния и дает на выходе не s₁, a s₀. Управляет, следовательно, в некотором смысле исходный автомат, и число его работающих состояний равно числу автоматов в конце работы. Аналогично можно получить цепочку из любого заданного числа автоматов.

Это очень простая модель с последовательным взаимодействием, и она показывает, что все взаимодействующие клетки должны точно соблюдать стадии развития, чтобы получился правильный результат.

Однако это пока модели накопления или простого роста, напоминающие модели Пенроуза с "кирпичами", сцепляющимися в прямые линии, а не модели развития. Поэтому посмотрим, можно ли так расширить растущие сет автоматов, чтобы они демонстрировали пространственную дифференцировку. Вопрос теперь состоит в том, как задать инструкции одному автомату, чтобы получилась сеть автоматов предписанной пространственной формы.

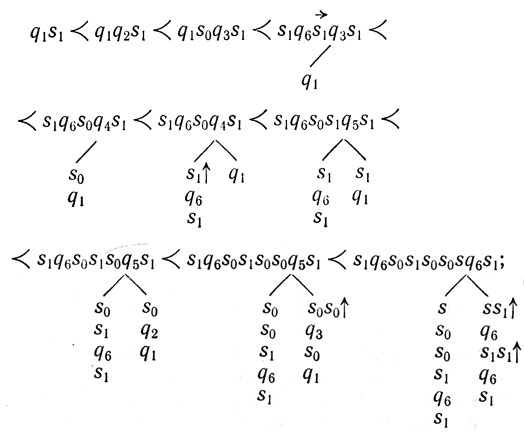
Чтобы показать, что это возможно, мы прежде всего приведем набор инструкций, из которого вырастает Х-образная сеть из пяти автоматов: один центральный соединен с четырьмя другими, а они могут сообщаться только через него. (Следовательно, мы говорим об Х-образно фигуре скорее в топологическом, чем в геометрическом смысле.) Если мы примем исходный автомат за центральный, то годится такой набор инструкций:

Мгновенные описания таковы:

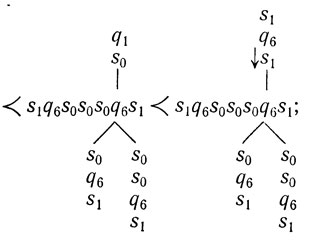
работа окончена.

Аналогично этому Y-образную фигуру из пяти автоматов дает набор инструкций:

Мгновенные описания таковы:

Итак, мы показали, что эти два вида фигур можно построить. Это, конечно, не означает, что нет других наборов инструкций, дающих те же фигуры, и один из них для Х-образной фигуры будет приведен ниже. (Это не исключает существования принципиально других способов получения заданных пространственных форм, и два таких способа будут указаны в разделе "Возможности для дальнейших исследований", гл. 8.)

В этих двух моделях в отличие от прямолинейных цепочек автоматов обратная связь существенна. Действительно, мы получили простейшую модель коллективного поведения, поскольку взаимодействие между автоматами обусловливает такое поведение каждого из них, которое при отсутствии этого взаимодействия было бы иным.

В связи с этим модели показывают очень важную вещь: при дифференцировке инструкции не обязательно должны утрачиваться, как считал Вейсман [2]. В этих моделях инструкции не претерпевают статических, "структурных" изменений: просто в ходе взаимодействия в системе на разных его стадиях действуют разные инструкции. И рост управляется изнутри благодаря тому, что одни и те же инструкции дают разные результаты на разных стадиях развития из-за различий в состояниях всей системы. То есть строящийся организм динамичен, он сам управляет своим поведением, в разные моменты проявляя разные свойства.

Однако, хотя таким образом демонстрируется развитие пространственной дифференцировки, требующееся для этого число инструкций слишком велико. В некотором смысле получающаяся сеть интуитивно кажется сложнее, чем исходный автомат. Но, с другой стороны, эти модели несколько громоздки, поскольку в реальных организмах вряд ли зиготы имеют больше состояний, чем зрелые особи - клеток. В случае линейных цепочек автоматов наименьшее число инструкций, необходимое для построения цепочки из n автоматов, было 2n-1 (и время их выполнения тоже было 2n-1). Наименьшее число состояний было n + 1. В случае Х- и Y-образных фигур и состояний тоже было на единицу больше, чем автоматов в конце работы, и для Y-образной фигуры потребовалось одиннадцать инструкций.

Но это не удивительно, если вспомнить, что машина Тьюринга имеет прежде всего теоретическое назначение, а не практическое и что ее истинный смысл в том, что она работает предельно детализнрованно, т. е. проделывает все шаги вычисления совершенно явно; в ней ценна скорее общность, чем скорость или экономичность. В организме вовсе не обязательно все инструкции должны быть так явно выделены, и в гл. 8 будет перечислен ряд способов, которыми организм может сокращать свой список инструкций и укрупнять шаги развития. Если бы мы интересовались в первую очередь скоростью и эффективностью, мы могли бы вернуться к моделированию на машине: например, там можно не писать специальную команду для каждой новой клетки, а поставить счетчик, определяющий, сколько будет клеток данного типа. Но в этой главе нас интересует главным образом логика, развития.

Тем не менее, однако, можно попытаться уменьшить число четверок, нужных для получения фигуры с данным числом автоматов.

Возвращаясь к простейшему случаю, когда автоматы располагаются в цепочку, мы замечаем, что ту же самую цепочку можно получить быстрее, если растить ее в двух направлениях одновременно. Чтобы показать это, вырастим цепочку из пяти автоматов, начиная с середины, а не с конца. Вот набор инструкций:

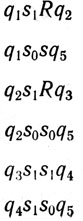
Мгновенные описания таковы:

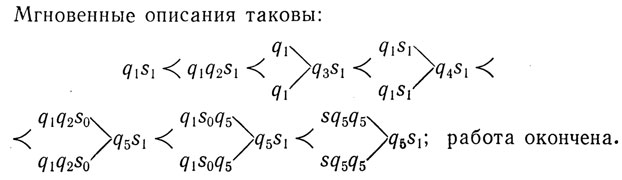
работа окончена.

Мы теперь не только обходимся пятью состояниями, но и число инструкций упало с 9 до 6. Если определить эффективность как отношение числа автоматов в конце работы к числу инструкций, то можно сказать, что эффективность возросла с ⁵/₉ до ⁵/₆.

Само по себе это не бог весть какое достижение, но, обобщая этот подход, можно получить гораздо больше. Например, можно предположить, что поскольку двухлинейное развитие оказалось более эффективным, чем однолинейное, то аналогичное четырехлинейное развитие будет еще эффективнее.

Получится, очевидно, Х-образная фигура, для которой мы теперь получаем новый способ построения; вот набор инструкций:

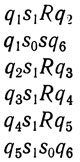
Мгновенные описания таковы:

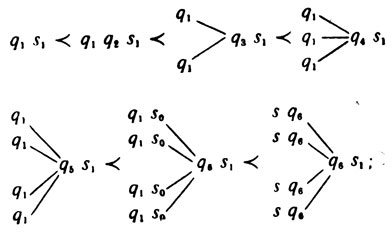
работа окончена.

Пока еще выгода невелика. Но если мы назовем каждую "линию" этой фигуры "строкой", а всякую совокупность автоматов, равноудаленных от начального, "столбцом", то сможем попытаться обобщить предыдущую модель, имеющую четыре строки и один столбец, увеличивая число строк и столбцов, и таким способом добиться большей эффективности. Например, сеть с двумя столбцами и четырьмя строками нам даст такой набор:

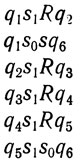
Мгновенные описания таковы:

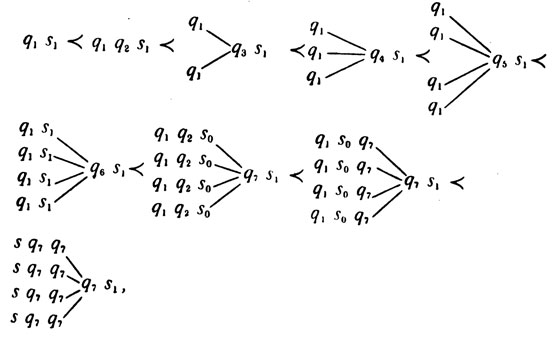
работа окончена.

Наконец-то мы получили действительно эффективную модель (в смысле, определенном выше), поскольку полученная сеть состоит из девяти автоматов, а каждый автомат имеет только восемь команд. Значит, эффективность теперь превышает 1, так как равна 1 ¹/₈.

При том же числе столбцов, равном двум, можно как угодно увеличить число строк, увеличивая число состояний по тому же принципу. Например, сеть из двух столбцов и пяти строк даст набор:

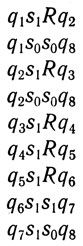
Нет смысла приводить мгновенные описания, поскольку принцип работы здесь точно такой же, как и в предыдущей модели.

Легко видеть, что эта фигура из двух столбцов может быть любого размера. То есть в каждом столбце может быть любое число автоматов, лишь бы число автоматов в одном столбце равнялось числу автоматов в другом. Мы получаем бесконечную последовательность фигур. Очевидно, что число инструкций, нужное для построения фигуры из этой последовательности, равно r + 2, где r - число автоматов в каждом столбце, т. е. число строк. Следовательно, с увеличением системы ее эффективность увеличивается и стремится к 2 при r→∞ (потому что имеются два столбца).

Но очевидно также, что, пока столбца только два, эффективность не может стать больше чем 2, и чтобы ее увеличить, надо увеличить число столбцов; каждый новый столбец увеличивает эффективность почти на единицу. Таким образом, эффективность стремится к пределу N при r→∞, где N - число столбцов.

Однако интересно, что, по-видимому, число столбцов нельзя увеличить, не увеличивая числа символов на ленте. Это означает, что если таких символов два (т. е. если каждый квадрат ленты несет один бит информации), то эффективность не может стать больше чем 2. Это означает также, что построение более сложных фигур требует больше одного бита информации на один квадрат. Для реальных организмов это может означать существование либо более чем двух возможных химических посредников в ситуациях, когда тот или иной из этих посредников всегда действует, либо более чем одного химического посредника в случаях, когда поведение клетки, к которой он адресован, определяется его наличием или отсутствием - как, например, произойдет, если этот посредник будет действовать подобно индуктору в модели Жакоба и Моно (приложение 4).

Более точная формулировка этого предположения такова: невозможно получить самоостанавливающуюся сеть автоматов, содержащую автоматы, удаленные более чем на два от исходного, если информация, которую они передают друг другу, бинарна, исключая случай цепочки автоматов, растущей с одного конца.

Это особенно интересно потому, что Тьюринг доказал, что для вычисления всех вычислимых чисел достаточно двух символов на ленте, и увеличение числа символов не увеличивает общности. Это означает также ограничение возможностей развития моделей типа Голдейкра и Бина (см. гл. 3).

Ни одна из сетей, приведенных до сих пор и имевших более одной строки (т. е. не цепочек), не содержала более двух столбцов. Но, конечно, если уже мы сможем получить определенное число столбцов, то число строк при этом может быть любым.

Чтобы показать, что, имея более двух символов на ленте, можно получить более двух столбцов, рассмотрим простейший случай: сеть из двух строк и трех столбцов. Ее порождает следующий набор:

Мгновенные описания ее:

работа окончена.

Седьмое мгновенное описание - решающее. Если бы в нем два автомата, находящихся в состоянии q₂, получили на входы s₁ от своих соседей, находившихся в предыдущий момент в состоянии q₃, то они породили бы еще два автомата. А если бы они получили s₀, то послали бы своим отпрыскам s₁, и тогда последний, находясь в состоянии q₁, породил бы два новых автомата. В обоих случаях развитие пошло бы не так, как мы хотели. Поэтому здесь понадобился новый символ s₂ и четверки

В качестве примечания к этому разделу, пожалуй, стоит заметить следующее. Хотя во всех приведенных здесь моделях все автоматы по окончании работы оказывались в своих конечных состояниях (кроме самой первой модели, где вообще не было конечного состояния), можно подобрать команды и так, чтобы развитие сетей останавливалось прежде, чем все автоматы успеют перейти в свои конечные состояния - работа остановится потому, что автоматы, не перешедшие в конечные состояния, не будут получать инструкций на вход. Однако, хотя в последних моделях это позволяет получить еще один столбец, все же дальнейшее увеличение числа столбцов при двух символах на ленте представляется невозможным.