В-6. Структура кибернетики

Известно несколько схем, представляющих структуру кибернетики. Наибольший интерес, по-видимому, представляет схема Ляпунова - Яблонского [Л. 19]. Приводимая ниже структура кибернетики была разработана в результате чтения курса кибернетики в Московском инженерно-физическом институте на протяжении нескольких лет [Л. 20]. Основным направлением этого курса служила трактовка положений кибернетики на инженерном уровне, предназначенном для подготовки инженеров-кибернетиков широкого профиля.

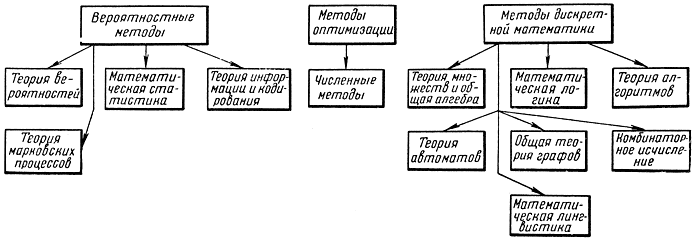
Рис. В-4. Математические основы кибернетики

Структура кибернетики в нашем понимании, в соответствии с которой предполагается излагать курс "Основы кибернетики", может быть разбита на четыре раздела:

1. Общие сведения о. кибернетике.
2. Математические основы кибернетики (рис. В-4).
3. Основы кибернетических моделей (рис. В-5).
4. Специальные и прикладные вопросы кибернетики (рис. В-6).

Математические основы кибернетики разделены на три цикла: вероятностные методы, методы оптимизации и численные методы, методы дискретной математики. Так как в основе исследования большинства систему управления лежат вероятностные методы, то первые три раздела вероятностных методов посвящаются теории вероятностей, математической статистике и теории марковских процессов. В разделе математической статистики в основном излагаются вопросы определения числовых значений характеристик случайных величин и законов распределения. Уже на примере этого раздела можно убедиться в том, что различные разделы кибернетики взаимно проникают друг в друга и резкого разделения провести не удается. Часто изложение теории вероятности производится с привлечением общей алгебры и математической логики, которые рассматриваются в разделе дискретной математики. Изложение математической статистики заканчивается теорией статистических решений, предлагающей математические методы для принятия решений в условиях неопределенности. Эти методы в значительной степени перекрываются методами теории игр.

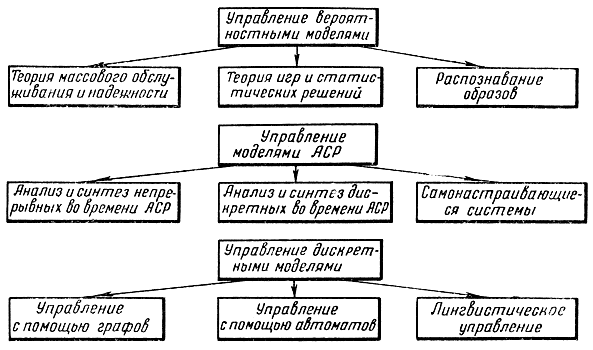
Рис. В-5. Основы кибернетических моделей

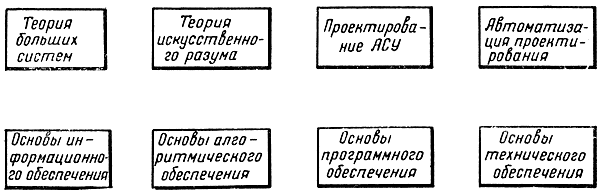
Рис. В-6. Специальные и прикладные вопросы кибернетики

Четвертый раздел вероятностных методов посвящен теории информации и кодирования. Наряду с рассмотрением вероятностного понятия информации, ее свойств и особенностей преобразования, развитых в теории связи, в этом разделе большое внимание уделяется другому подходу к информационным явлениям, который сформировался в связи с машинной обработкой информации и внедрением АСУ и в котором используется понятие информационного тезауруса.

Оптимальные методы обработки, передачи, преобразования и защиты информации существенным образом зависят от способов ее кодирования, которым уделяется большое место в этом разделе. Для 'построения оптимальных систем управления необходимо иметь в наличии математический аппарат для отыскания оптимальных законов управления, который составляет основное содержание второго цикла математических основ кибернетики. В зависимости от специфики системы управления могут применяться различные методы оптимизации: от классических методов Эйлера - Лагранжа, динамического программирования и принципа максимума Понтрягина до методов математического программирования. При этом рассматриваются непрерывные и дискретные, детерминированные и вероятностные варианты этих методов. Очень часто для отыскания оптимального управления приходится решать численными методами дифференциальные, интегральные или разностные уравнения, которые составляют в настоящее время самостоятельный большой раздел прикладной математики. Учитывая использование ЭВМ, желательно окончательные численные процедуры отыскания решения записывать с помощью какого-нибудь проблемно-ориентированного языка типа АЛГОЛ или ФОРТРАН.

Особого внимания заслуживает третий цикл математических основ кибернетики - дискретная математика (см. рис. В-4). Как уже указывалось, большинство процессов управления, особенно в АСУ, дискретные. Массивы информации и программы, записанные на машинных носителях дискретны по своей структуре. В редких случаях их можно описать с помощью аппарата непрерывной математики (дифференциальных уравнений). Поэтому для инженера - специалиста по управлению требуется другая математическая подготовка по сравнению с той, которая дается в настоящее время в технических вузах. Ему необходимо знать дискретную математику, которая называется так потому, что в ней нет понятия непрерывности, дифференцируемости. Дискретная математика включает следующие разделы: теорию множеств и общую алгебру, математическую логику, теорию алгоритмов, теорию автоматов, теорию графов, комбинаторное исчисление, математическую лингвистику.

Все кибернетические модели, рассматриваемые в третьей структурной (см. рис. В-5), разделены на три группы. Здесь первую группу составляют модели, в основе которых лежит вероятностная природа. Это - модели теории массового обслуживания, теории игр, распознавания образов. Вторая группа объединяет кибернетические модели, поведение которых описывается дифференциальными или разностными уравнениями. Большинство методов исследования таких систем излагается в работах по системам автоматического регулирования. Для этих методов характерно рассмотрение процессов во времени, поэтому такие модели могут быть названы динамическими системами. Третью группу кибернетических моделей составляют дискретные кибернетические модели. Эти модели применяются и для исследования процессов управления, протекающих во времени, но в основном в них время не используется. Например, требуется с помощью вычислительных машин раскроить листовое железо для обшивки корабля наилучшим образом с точки зрения расхода материала, причем время, в течение которого производится раскрой, не имеет значения. Здесь с успехом применяются как детерминированные, так и вероятностные методы расчета. Рассматриваемые в этой группе методы наиболее слабо освещены в литературе и представляют собой наибольшую ценность. В этой же группе имеется третий раздел, посвященный лингвистическому управлению.

В общей структурной схеме кибернетики предусматривается еще четвертая часть, посвященная специальным и прикладным вопросам кибернетики (см. рис. В-6). Содержание этой части выглядит наиболее неопределенным, так как ее название допускает включение самых разнообразных разделов. Вопросы, связанные с проектированием АСУ, выделены в самостоятельный раздел. Хотя они и представляют модификацию больших систем, для них характерен человеко-машинный способ управления. В этом разделе в основном рассматриваются общие вопросы проектирования АСУ и особенности проектирования функциональных подсистем.

Раздел, названный "Теория искусственного разума", включает различные аспекты теории принятия решений в больших системах, а также вопросы создания информационно-программных комплексов, моделирующих профессиональный искусственный разум. Необходимость введения самостоятельного раздела по автоматизации проектирования диктуется тем обстоятельством, что в ближайшие годы любое проектирование, в том числе АСУ и ЦВМ, немыслимо без автоматизации.

Вторая группа разделов этой части посвящена так называемым обеспечивающим подсистемам систем управления. Хотя концепция обеспечивающих подсистем возникла в процессе разработки АСУ, она полностью применима к любым системам управления. Для любого управления нужны данные об объекте управления, которые могут обновляться в процессе управления, а также различные модели преобразования информации в системе, что и составляет основное содержание информационного обеспечения. Начало проектирования начинается с системного обследования и составления технического задания, после чего составляются математические модели управления (кибернетические модели). Если модель использует дифференциальные уравнения, то необходимо, применяя численные методы, их "арифметизировать", чтобы получить процедуру вычисления решений для конкретных числовых начальных условий, использующую четыре арифметические действия и другие элементарные машинные операции, которая и рассматривается как алгоритм решения задачи. При решении задачи планирования с помощью линейного программирования (к примеру) в качестве математической модели выступает модель задачи оптимизации в виде линейного программирования, а алгоритм представляет конкретную процедуру отыскания решения этой задачи. При наличии алгоритма в принципе решение может быть получено ручным способом, однако в большинстве случаев требуются вычислительные машины, и необходимо по алгоритмам составить программы вычислений на ЦВМ, которые составляют часть программного обеспечения системы. Три раздела: математические модели, алгоритмическое и программное обеспечение - составляют содержание математического обеспечения.

Основным техническим средством является ЦВМ. При проектировании технического обеспечения в этой части поступают двояким образом: или разрабатывают специализированную управляющую машину, как часто бывает при управлении непрерывными объектами, или останавливаются на определенной системе ЦВМ, допускающей модульный синтез конкретной ЦВМ, что характерно для АСУ на данном этапе. В этом последнем случае из машинно-ориентированного программного обеспечения (операционной системы и т. д.), широко используя режимы генерации, создают программное обеспечение (главным образом операционную систему), ориентированное на конкретную систему, для которой создается АСУ. Помимо ЦВМ при проектировании технического обеспечения требуется определить состав при наличии модульного исполнения или спроектировать терминальные устройства и линии связи. При разработке программного обеспечения кибернетик должен знать с позиций пользователя имеющиеся в его распоряжении машинно-ориентированные системы программирования, уметь создавать из них "дочерние" проблемно-ориентированные системы программирования и дорабатывать их в процессе эволюции системы управления, что особенно важно для АСУ.

В связи с этим можно было бы добавить еще пятую структурную часть, посвященную методам программирования на ЦВМ, начиная от методов программирования в кодах машины, списковых структур и кончая алгоритмическими языками и метаязыками. Хотя в строгом смысле этот раздел носит самостоятельный характер и не включается в кибернетику, большинство деловых методов кибернетики так тесно переплетается с вопросами программирования и интерпретации на ЦВМ, что очень трудно бывает разделить, где "чистое программирование", а где "чистая кибернетика". Знание методов программирования для инженера-кибернетика обязательно, однако по установившейся традиции в высшей школе они изучаются независимо и вне кибернетики.