3-2. Критерии согласия

Рассмотрим два критерия согласия: критерий χ² Пирсона и критерий Колмогорова. Начнем с простейшего случая. Допустим вначале, что случайная величина X может принимать только два значения с вероятностями p₁ и p₂, причем

Пусть проведено n опытов, ν₁ раз величина приняла первое значение (попала в группу S₁) и ν₂ раз - второе (попала в группу S₂), причем

Необходимо определить достоверность (вероятность) гипотезы о возможности замены вероятностей p₁ и p₂ частотами p*₁=υ₁/n и p*₂=υ₂/n

За меру ошибки возьмем взвешенную сумму квадратов отклонений ν₁ и ν₂ от их математических ожиданий np₁ и np₂:

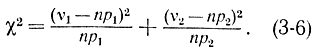
В качестве весов слагаемых в этой формуле выбраны величины, обратные математическим ожиданиям. Формулу (3-6) можно переписать в виде

где

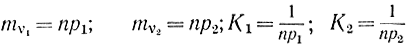
или

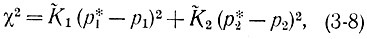
где

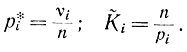
Величины

являются зависимыми. Действительно, в соответствии с формулами (3-4) и (3-5)

откуда

Взвешенные отклонения

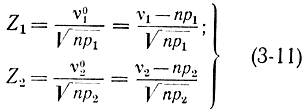
и в соответствии с соотношением (3-10) будут также связаны следующей зависимостью:

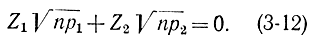
С учетом равенств (3-11) выражение (3-6) можно преобразовать к виду:

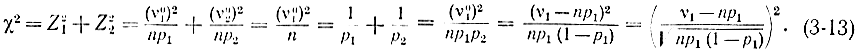
Но согласно теореме Лапласа случайная величина 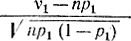при большом n распределена примерно по нормальному закону. Следовательно, квадрат этой величины (величина χ²) распределен по закону χ² с одной степенью свободы. Выберем какое-нибудь значение доверительной вероятности р=0,01, которая в теории проверки статистических гипотез называется уровнем значимости, и найдем по таблицам χ²-распределения соответствующее этой вероятности значение величины χ²=χ²_0,01. Очевидно, что наша гипотеза о том, что можно определить вероятность через частоты, будет неверна, если вычисленное значение χ²₁ будет больше χ²_0,01. Точнее, в этом случае равенство между частотой и вероятностью будет нарушаться с вероятностью большей, чем р=0,01. В таблицах χ²-распределения для каждого χ² приведены значения вероятности

Эта функция - убывающая функция аргумента χ². Она связана с функцией распределения χ² определяемой формулой

соотношением

Такая система таблиц принята для удобства проверки статистических гипотез в ущерб теории оценок.

Рассмотренную выше задачу можно распространить на случай l групп и l вероятностей. Пусть имеется l групп: S₁, S₂, ..., S_n возможных значений случайной величины (или признака). Выдвигаем гипотезу, что можно определить значение вероятностей р₁, р₂,...,p_l (где ) для попадания в каждую группу путем определения частот. Пусть в результате n опытов число попаданий в каждую группу составляет соответственно υ₁, υ₂,..., υ_l, причем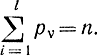

Рассмотренная задача полностью включает в себя определение закона распределения по гистограмме; в этом случае группы S_i - это разряды J_i=(υ_i, υ_i+1); p_υ - истинные вероятности попадания в данный интервал. Для количественной оценки точности согласия экспериментальных данных с некоторым гипотетическим законом распределения используем взвешенную сумму квадратов отклонений υ⁰_i=υ_i-np_i или величин p*_i-p_i

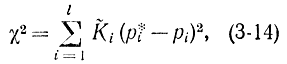
где

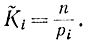
Это соотношение можно переписать в виде

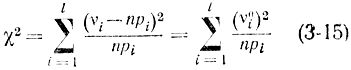
или

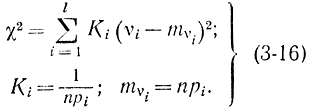
Как и в рассмотренном случае, отклонения υ⁰₁ связаны линейным соотношением

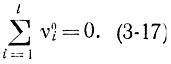
В предыдущем примере случайные числа vt подчинялись биномиальному закону распределения, который может быть записан в виде

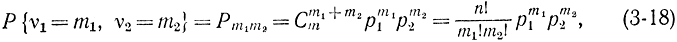
где m₁+m₂=n. В случае l групп (или интервалов) числа ν_i- подчиняются полиномиальному закону распределения [Л. 26], который является обобщением биномиального закона

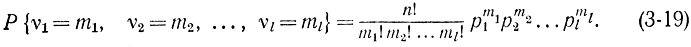
На этот случай может быть распространена и теорема Лапласа, которая утверждает, что нормированные отклонения

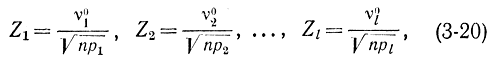
связанные одним линейным соотношением (3-17), подчиняются (l-1)- мерному нормальному закону [теорема Лапласа для (l-1)-мерного случайного вектора]. Отсюда следует, что величина

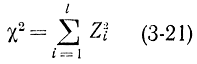
распределена по закону χ² с l-1 степенями свободы (строгое доказательство этого положения приведено у Крамера [Л. 22]).

В результате имеем следующую процедуру проверки статистической гипотезы. По рассчитанному в соответствии с гипотетическим законом распределения χ²₁ определяют вероятность появления значений χ², больших χ²₁:

Предположим, что получен другой гипотетический закон распределения, который лучше согласуется с экспериментом, чем первый вариант. Тогда для него сумма взвешенных квадратов будет меньше χ²₁, т.е. χ²₂<χ²₁. Вероятность этого события Р(χ²₂<χ²₁} должна быть мала, тогда первый вариант гипотетического закона распределения лучше. Но так как

то гипотетический закон распределения тем лучше, чем выше вероятность (3-22), соответствующая рассчитанному χ²₁.

Следует сделать несколько замечаний о методике применения критерия χ². Предположим, что по экспериментальным данным значения χ² получаются такими малыми, что значений, больших полученных, теоретически можно ожидать с вероятностью, близкой к единице [р(χ²)=0,99]. Такое хорошее совпадение заставляет думать о некачественном выполнении эксперимента и предварительной обработки данных. Имеется в виду распространенная на практике "подчистка" результатов эксперимента, которая состоит в том, что некоторые результаты субъективно отбрасываются или округляются. Если получилось, что для данного уровня значимости р условие χ²₁<χ²_p, где χ²₁ - экспериментально вычисленное значение, не выполняется, то необходимо проверить экспериментальные данные и повторить эксперимент. Если при повторном эксперименте это условие опять не удовлетворяется, то необходимо отбросить гипотезу, т. е. изменить параметры закона распределения или выбрать другой закон.

Все наши рассуждения справедливы при большом n, так как теорема Лапласа имеет предельный характер (только при n→∞ и большом числе значений, попадающих в каждый разряд, величины Z_i распределены по нормальному закону). На практике рекомендуется иметь не менее 5-10 значений в каждом разряде. Если число этих значений мало (один-два), то рекомендуется укрупнить разряды, сделав число их меньше.

Наконец, несколько слов о числе степеней свободы. Величины 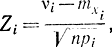, входящие в сумму (3-21), должны быть независимы друг от друга. Только при этом условии (и нормальном законе их распределения) сумма их квадратов подчиняется распределению χ². Поэтому число степеней свободы этого распределения равно числу величин Z_i (число разрядов l) минус число связей, наложенных на Zi, или ν_i. Одно условие (связь), определяемое соотношением (3-17), накладывается всегда, его можно записать в виде

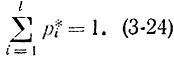
При этом следует иметь в виду, что

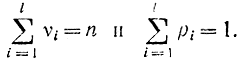
Если подбирается гипотетическое распределение с условием, чтобы совпадали теоретическое математическое ожидание m_x и его оценка по экспериментальным данным, то накладывается еще условие

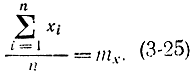
Предполагая, что в каждом разряде случайная величина сохраняет постоянное значение (в соответствии с гистограммой), равное среднему на этом разряде значению

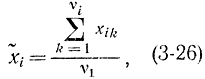
можно формулу (3-25) записать в виде

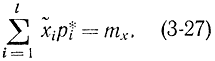
С учетом условий (3-24) и (3-27) число степеней свободы теперь будет r=l-2.

Если распределение определяется при условии выполнения соотношения (3-27) и совпадении теоретической дисперсии и ее оценки, то добавляется третье условие:

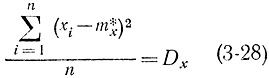
или

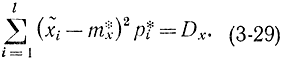
При добавлении этого условия число степеней свободы будет r=l-3.

Пример 3-3. Для условий примера 3-1 проверим статистическую гипотезу о нормальности закона распределения при условии, что математическое ожидание и среднеквадратичное значение этого распределения равны оценкам этих величин m=1,160; σ=0,167.

Вероятности попадания в разряды, которые выбраны в примере 3-1, находим по формуле (см. приложение 1)

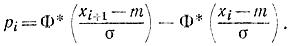
Далее подсчитываем np_i (при n=200). Результаты сведены в табл. 3-4.

Таблица 3-4

Используя полученные результаты, получаем:

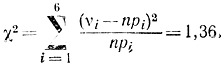
Затем определяем число степеней свободы r=l-3=6-3=3 и с помощью таблиц χ²-распределения (см. приложение 2) устанавливаем, что найденное значение χ² соответствует р=0,73. Следовательно, можно утверждать, что с вероятностью р=0,27 на практике отклонения могут быть больше наблюденных. Этот результат можно считать вполне удовлетворительным.

Если закон распределения F(х) известен полностью (т. е. и вид функции распределения и числовые значения параметров известны), то можно применять критерий согласия Колмогорова, который проще критерия χ². В критерии Колмогорова за меру качества согласования экспериментального и теоретического распределения принимается максимальное значение модуля разности между этими функциями

Оказывается, что благодаря теореме Колмогорова, легко вычислить функцию распределения вероятности для величины D. Доказано, что какова бы ни была функция распределения F(х) непрерывной случайной величины X, при неограниченном числе n независимых наблюдений вероятность неравенства

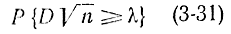
стремится к пределу

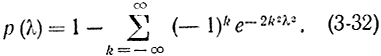
Заметим, что функция (3-31) опять убывающая и равна единице минус функция распределения величины :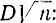

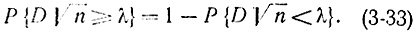
Процедура проверки согласия по этому критерию аналогична проверке по критерию χ². По формуле (3-30) вычисляется D, а затем определяется величина

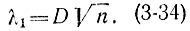
Далее рассуждаем следующим образом. Допустим, что за счет каких-то причин (лучшего подбора закона распределения) получилось

Тогда этот закон будет'лучше гипотетического. Чем меньше вероятность события (3-35), тем лучше наш закон, который соответствует λ₁. Учитывая (3-33), можно сказать, что чем выше вероятность (3-31), тем лучше согласование.

Критерий Колмогорова значительно проще критерия χ². Однако для его применения необходимо иметь график или таблицы теоретического закона распределения, т. е. он должен быть полностью задан. На практике это редко бывает. Чаще известен только вид закона и требуется определить его параметры. В случае применения критерия χ² это учитывается изменением числа степеней свободы. Если внимательно изучить таблицы χ²-распределения, нетрудно убедиться, что чем больше степеней свободы, тем больше значение вероятности. Следовательно, если не учесть уменьшения числа степеней свободы, то вероятности будут больше и мы ошибочно примем гипотезу, тогда как на самом деле она несправедлива. Поэтому, если при неизвестных параметрах закона распределения применить критерий Колмогорова, взяв за значения параметров его оценки, также получим завышенный результат, так как эта процедура будет эквивалентна применению критерия без учета уменьшения степеней свободы, т. е. по этому критерию гипотеза будет признана допустимой, а на самом деле она несправедлива.

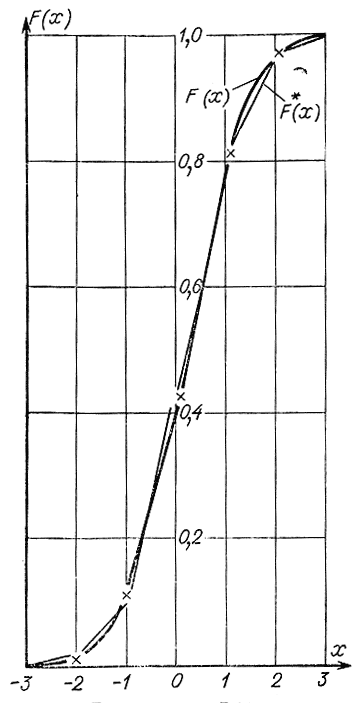
Рис. 3-3. Теоретическая F(x) и F*(x) экспериментальная функции распределения для примера 3-4

Для распределения Колмогорова составлены подробные таблицы (приложение 5). Оба критерия (χ² и Колмогорова) часто применяются для проверки закона распределения чисел, которые получаются при моделировании на ЦВМ по методу Монте-Карло.

Пример 3-4. Применим критерий Колмогорова для определения степени согласия закона распределения случайной величины, фигурировавшей в трех предыдущих примерах, нормальному закону распределения с параметрами, равными оценкам:

Систематизируем (табл. 3-5) полученные данные.

На рис. 3-3 представлены теоретическая F(х) и экспериментальная F*(х) функции распределения в виде кривой и ломаной линий. В случае критерия Колмогорова следует использовать непосредственно статистический ряд, так как при ступенчатой аппроксимации функции распределения ее кривая существенно зависит от выбора величины разряда.

Из табл. 3-5 определяем параметр

По формуле (3-34) находим:

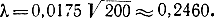
С помощью таблиц функции р(λ), приведенных в приложении 5, находим?

Как и следовало ожидать, это значение вероятности больше, чем рассчитанное по критерию χ².

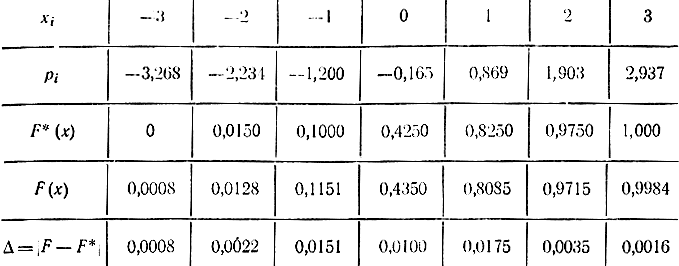
Таблица 3-5