3-1. Понятие статистического ряда и гистограммы

При экспериментальных замерах можно строить таблицу значений случайной величины (табл. 3-1), но такое представление громоздко. Более удобны статистический ряд и гистограмма [Л. 21].

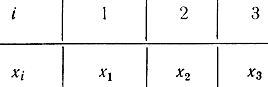
Таблица 3-1

При построении статистического ряда возможный интервал изменения случайной величины X разбивается на конечное число участков, необязательно одинаковой величины. В одну строку или колонку (табл. 3-2) заносятся значения концов интервала (x_i, x_i+1); в другую - частоты попадания случайной величины в данный интервал р*_i=ν_i/n, т. е. отношения числа попадания случайной величины в данный интервал к общему числу опытов.

Таблица 3-2

Как выбираются величины интервалов при составлении статистического ряда, будет объяснено ниже.

Пример 3-1. У 200 студентов спросили, достаточно ли им стипендии на месяц. Оказалось, что одни берут в долг до трех рублей (эти цифры берутся со знаком минус), а другие экономят. Результаты опроса сведены в статистический ряд (табл. 3-3), где случайная величина X равна остатку от стипендии к концу месяца.

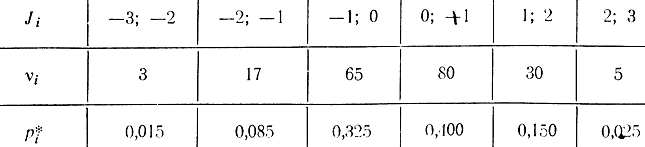
Таблица 3-3

Если случайная величина X попадает на границу разряда, то условно можно добавлять к ν_i в каждом разряде по 1/2.

Статистический ряд удобно оформить графически в виде гистограммы (рис. 3-1). По оси абсцисс откладываются значения случайной величины, отмечаются значения концов интервалов (x_i, x_i+1). На каждом из разрядов, как на основании, строится прямоугольник, площадь

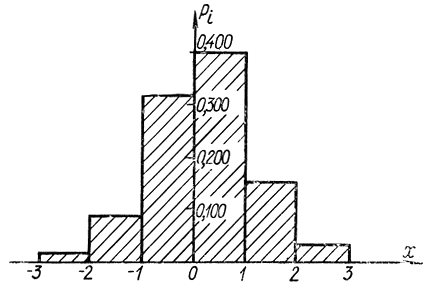
Рис. 3-1. Гистограмма случайной величины

которого равна частоте попадания случайной величины в данный разряд. Получается ступенчатая кривая, причем ордината каждой ступеньки равна соответствующей частоте, деленной на ширину интервала (величину разряда). Число разрядов не должно быть очень большим и очень маленьким. Обычно используют 10-20 разрядов. Величины разрядов всего удобнее выбирать одинаковыми, но при большой неравномерности закона распределения целесообразно разряды брать меньше в области быстрого изменения плотности распределения. Гистограмма приближается к кривой плотности распределения вероятности при увеличении числа опытов и соответствующем уменьшении величины разрядов. С помощью статистического ряда можно построить (рис. 3-2) приближенно функцию распределения вероятности F(х):

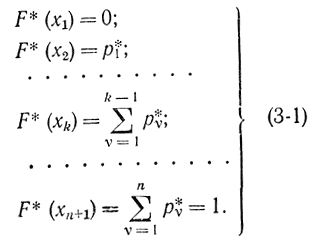
Часто требуется провести кривую плотности распределения при наличии экспериментально снятой гистограммы. Если вид закона распределения полученных случайных величин известен, то самый простейший способ - это вычислить оценки для моментов и взять в законе распределения параметры такие, чтобы теоретически моменты совпадали с оценками.

Пример 3-2. В табл. 3-3 приведены данные по остаткам от стипендии студентов к концу месяца. Естественно считать, что исследуемая величина X возникает после суммирования результатов независимых остатков от элементарных затрат, тогда из теоретических соображений можно считать, что величина X подчиняется нормальному закону распределения

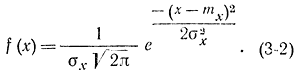
Требуется подобрать параметры m_x и σ_х так, чтобы функция f(x) наилучшим образом описывала данный статистический материал. Для данного случая оценки D*_x и m*_x имеются следующие значения:

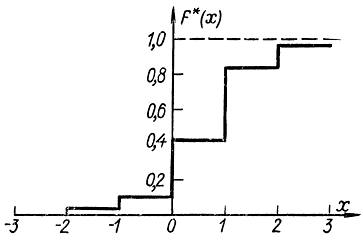
Рис. 3-2. Кривая функции распределения

Согласно методу моментов параметры m_x и σ_x теоретической кривой f(х) выбираем совпадающими с соответствующими оценками m_x* и σ_x*. Подставляя эти величины в формулу (3-2), получаем:

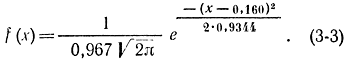
Однако при этом методе остается неясным, какова количественная оценка величины ошибки при такой замене. Количественную оценку удается сделать с помощью так называемых критериев согласия [Л. 21, 25, 26].