а) Свойства критерия Неймана-Пирсона
В ряде случаев весьма желательно, чтобы обе вероятности α и β были малы. Однако при конечном фиксированном объеме выборки n и различных значениях Е1 нельзя одновременно получить малые α и β, так как уменьшение одной влечет за собой,увеличение другой величины. При фиксированном n и α процедура Неймана - Пирсона позволяет выбрать такое 1Е, для которого В=1-β будет максимальным (т. е. β минимально). Аналогичным образом можно показать, что эта процедура обеспечивает Е1 с минимальным а при заданных β и n или с минимальным n при фиксированных α и β. Фиксация двух параметров отражается на выборе порога С. Оказывается, что все эти величины связаны между собой [Л. 34, 37]. В каждом из этих трех случаев величина С является функцией двух фиксированных параметров: С(n,α); С (β, n); С (α,β). Отношение
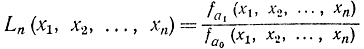
называется коэффициентом правдоподобия, который зависит от n выборочных значений xi случайной величины X. Условно при fa1=fa0=0 полагается Ln=1. Классическая теория проверки статистических гипотез развита для случая однородной независимой выборки, когда независимы друг от друга и являются реализациями одной и той же случайной величины X с плотностью распределения fa(х). Поэтому
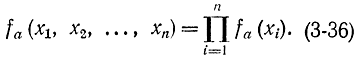
Отсюда, если прологарифмировать соотношение
Ln≤C,
которое определяет область E0, а значит, и выбор гипотезы Н0 в случае применения критерия Неймана-Пирсона, получим:

где
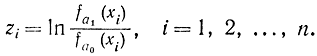
Величины zi являются реализациями функции
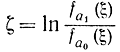
случайной величины ζ с плотностью распределения вероятности fa(х). Поэтому ln является реализацией случайной величины
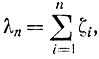
которая представляет собою сумму независимых, одинаково распределенных случайных величин. Отсюда в соответствии с ЦПТ распределение случайной величины λn подчиняется при большом n нормальному закону, т. е.
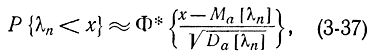
где
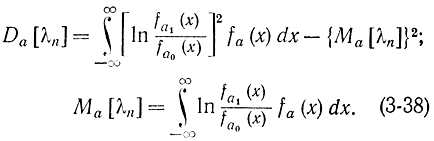
Полагая x=ln С = nc, получаем:
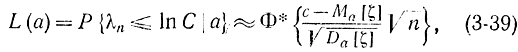
так как
M[λn]=nM[ζi]
D[λn]=nD[ζi]
Функция L(а), равная вероятности принятия гипотезы H0, когда истинное значение параметра равной a и x=lnС, называется операционной характеристикой. Она позволяет вычислять вероятность правильного выбора между гипотезами при заданном значении параметра .а и связана простыми соотношениями с величинами α и β.
Так как ошибка первого рода происходит, когда вместо гипотезы H0 (т. е. при истинном значении параметра а=а0) принимается гипотеза H1 то согласно условию λn≥lnC
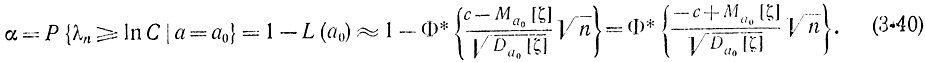
При этом учтено, что Φ*(-х)=1-Φ*(х).
Аналогичным образом в соответствии с тем, что ошибка второго рода происходит, когда вместо гипотезы Н (т. е. при истинном значении параметра a=a1) принимается гипотеза #0, согласно условию λn<>lnС имеем:
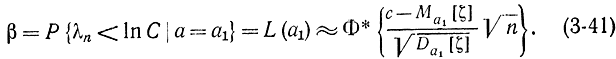
Введем функцию, обратную вероятностной функции Φ*(х),
tp=argΦ*,
причем величина tp называется p-квантилем нормального распределения, так что
Φ*(tp)=p.
В соответствии со свойством функции нормального распределения
-tр=t1-p
Тогда с помощью соотношений (3-40) и (3-41) можно получить следующие формулы:
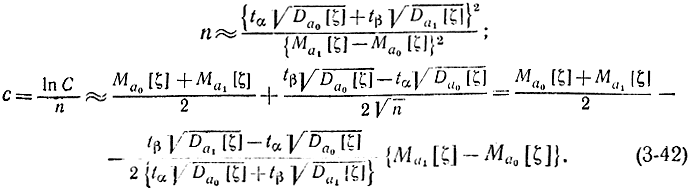
Если подставить эти выражения для n и c в формулу (3-39), получим:
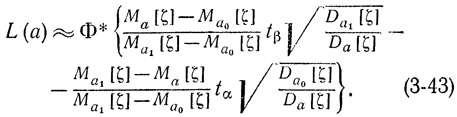
Полагая в этом соотношении соответственно a=a0 и a=a1 получаем:
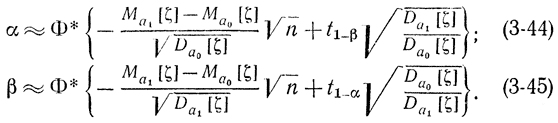
Если величина X подчиняется нормальному закону распределения, то fa(х) становится нормальной плотностью распределения. При этом соотношения (3-44) и (3-45) становятся точными. Если использовать асимптотическую формулу для нормального закона
Φ*(-х)≈ехр(- х2/2),
справедливую при x→∞, из (3-44) при n получим следующее соотношение:
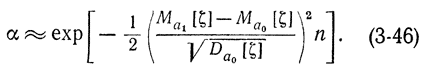
Аналогичным образом, если зафиксировать а в формуле (3-45), при n→∞ получим:
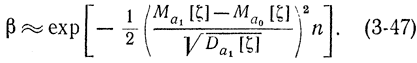
С помощью соотношений (3-46) и (3-47) нетрудно убедиться, что при фиксировании одной вероятности α или β другая убывает с ростом n по экспоненциальному закону, а при больших n величины α и β не зависят друг от друга. Можно показать [Л. 34], что предельные соотношения (3-46) и (3-47) справедливы для любого закона распределения fa(х) величины X.
Получим связь между параметрами при классической процедуре в случае нормального закона распределения
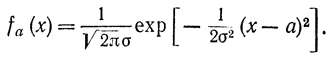
Тогда многие ранее полученные формулы в силу нормального закона станут точными.
Возможны три варианта задачи проверки статистических гипотез: известна σ, параметр а неизвестен; σ неизвестна, параметр a известен; оба параметра а и σ неизвестны. Для простоты рассмотрим только случай известной дисперсии σ2.
Логарифм коэффициента правдоподобия ln определится по формуле
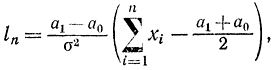
логарифм элементарного коэффициента правдоподобия - соотношением
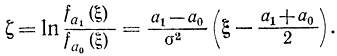
Так как эта величина является линейной функцией ζ и последняя распределена нормально, то величина ζ также будет иметь нормальный закон распределения с математическим ожиданием
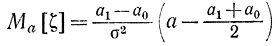
и дисперсией
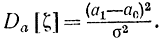
Подставив эти выражения в формулы (3-42) - (3-45), получим:
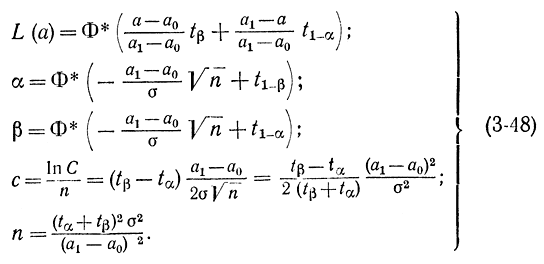
Из первого соотношения может быть сделан неправильный вывод о независимости операционной характеристики от n. Эта зависимость неявная, так как в соответствии со второй и третьей формулами a1 и a0 при заданных α и β зависят от n. Процесс вычислений производится в следующей последовательности: по заданным α и β с помощью второй и третьей формул определяют значения a0 и a1, зная которые, вычисляют все остальные характеристики. Иногда вместо величины ln рассматривают величину
l'n=∑xi
тогда все соотношения останутся прежними, если заменить величину С на С', определяемую по формуле
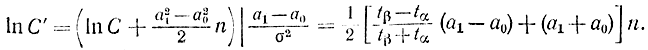
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'