б) Последовательный критерий Вальда
В отличие от классического критерия Неймана-Пирсона последовательная процедура Вальда не предусматривает заранее фиксированного объема выборки n и решение о прекращении испытаний выносится в зависимости от проведенных испытаний [Л. 34, 37].
В критерии Вальда, являющемся обобщением классической процедуры, на каждой стадии эксперимента совокупность всевозможных выборок Rn объема n разбивается на три не пересекающихся множества E0(n),E(n)*,E(n)1. При попадании выборки Х=(х1,..., хn) в множество E1(n) принимают гипотезу H0, испытания заканчивают; при попадании в множество Е(n)1 принимают гипотезу Н1 и испытания заканчивают. В случае попадания выборки в область E*(n) не принимают ни одной гипотезы, а производят следующее испытание xn+1 и анализируют аналогично предыдущему выборку (х1, х2, ..., хn, хn+1).
Нетрудно убедиться, что в процедуре Вальда объем выборки n является случайной величиной. Поэтому естественно за лучшую (оптимальную) процедуру построения областей Е(n)0, E*(n), E(n)1 принять такую, которая при одних и тех же аир имеет по сравнению с другими процедурами минимальное среднее значение n, т. е. М[n]=min.
Можно показать, что классическая процедура является частным случаем последовательной процедуры. Для этого достаточно выбрать следующее правило образования области E(n)*:
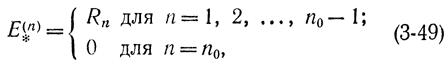
где n0 - заданный заранее объем выборки; Rn - совокупность всевозможных выборок объема n; 0 - пустое множество. Соотношение (3-49) означает, что решение принимается только на n0-м шаге и классическая процедура является частным случаем процедуры Вальда с n0=М[ν], где ν - случайное число испытаний. Оказывается, что последовательная процедура может обеспечить при тех же самых α и β, меньшее значение М[ν], чем соответствующее классическое число n0. Вальдом найдена оптимальная последовательная процедура определения областей E(n)0, E1(n), E(n)*, когда заданы вместо одного порога С, как в классической процедуре, два порога А и В.
Область Е(n)0 задается неравенством
Ln(x1,x2,..., xn)≤В.
В этом случае принимается гипотеза Н0 и испытания прекращаются. Область Е(n)0 определяется неравенством
В<(x1, x2, ..., xn)<L.
Если выборка удовлетворяет этому соотношению, то испытания продолжаются. И, наконец, область Е(n)1 определяется соотношением
A≤Ln(x1, х2, ..., хn).
В этом случае принимается гипотеза Н1 и испытания прекращаются.
функция Ln(х1, х2, хn), как и в классической процедуре, определяется формулой
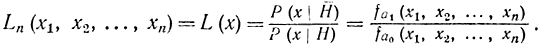
Для однородной независимой выборки и двух значений параметра a=a0a=a1 Вальдом доказана оптимальность последовательной процедуры, обеспечивающая М[ν]=min, и найдены связи между параметрами а, а0, а1, α,β, A, B, M[ν] |3, А, В, М М.
Операционная характеристика [Л. 34] в последовательной процедуре имеет вид:
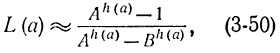
где h(а) является корнем уравнения
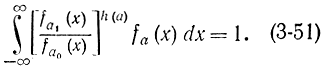
Здесь A и B - два порога для коэффициента правдоподобия Ln(x1, x2,..., xn), причем в соответствии с определением α, β, Ln имеем:
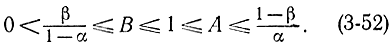
Эти соотношения можно пояснить следующим образом. По определению коэффициент правдоподобия Ln равен отношению вероятностей того, что данная выборка соответствует гипотезе H1 или H0, т. е.
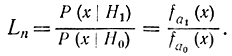
Согласно последовательному критерию вероятность выборки (x1, х2, хn), приводящей к принятию гипотезы Н1 (и отклонению Н0), по крайней мере в А раз больше при гипотезе Н1 чем при H0:
Р(х|Н1)≥АР(х|Н0), (3-53)
так как Н1 принимается при условии
Ln≥A.
Допустим, произведена последовательная процедура оценки гипотез H0 и H1. При этом получилась последовательность выборок какого-то объема. Рассмотрим подмножество этих выборок, которые приводили к гипотезе H1 и зададимся целью определить вероятность того, что последовательный процесс выбора закончится принятием гипотезы Н1 (отклонением Н0). Эта вероятность по определению равна или меньше а в случае, когда на самом деле имеет место гипотеза Н0, и равна или меньше 1-β, если на самом деле имеет место гипотеза H1 Последнее положение следует из того, что по определению вероятность принятия H0, когда верна H1 равна β. Так как имеется доказательство сходимости последовательной процедуры за конечное число шагов n с вероятностью, равной единице [Л. 37], то можно утверждать, что вероятность отклонения H0 (принятия H1), когда верна H1, должна быть равна 1-β. Но так как на каждом шаге, включая последний, справедливо соотношение (3-53), то можно утверждать, что 1-β≥Aα или
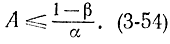
Отсюда следует, что величина (1-β)/α является верхней границей для А.
Аналогичным образом доказывается, что
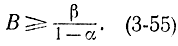
Действительно, вероятность получения любой заданной выборки (х1, х2, ..., хn), приводящей к принятию H0 (отклонению H1), при гипотезе H0 по крайней мере в 1/В раз больше вероятности получения этой выборки, когда верна H1 т. е.
Р(х|Н1)≤ВР(х|Н0),
так как гипотеза H0 принимается, когда
Ln≤B,
следовательно, и вероятность принятия H0 при гипотезе H1 тоже по крайней мере в 1/B раз больше вероятности принятия H1 Так как первая вероятность равна β, а вторая 1-α, то получаем соотношение (3-55), которое утверждает, что нижней границей величины В является β/(1-α). Можно также пояснить условия того, что пороги А и В удовлетворяют соотношениям
A≥1, 0<B≥1. (3-56)
Действительно, в отсутствие шумов разумным решением было бы принимать гипотезу H1 всякий раз, когда
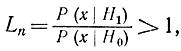
и гипотезу H0 в случае Ln<1, так как выбор целесообразно делать в пользу той гипотезы, вероятность которой больше. В этом случае A=B=1. Однако в случае наличия шумов или когда гипотезы Н1 и H0 перекрываются, получается зона неопределенности, требуется увеличить A и уменьшить В по сравнению с единицей. Зона неопределенности будет определяться величиной A-B. Эта зона подлежит дальнейшему исследованию.
При двупороговой, последовательной процедуре величины порогов определяются статистикой шумов, самой выборкой и величинами α и β. На практике за величины порогов могут быть взяты их границы, т. е.
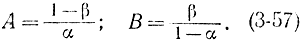
Следует заметить, что классическая и последовательная процедуры могут применяться в одних и тех же случаях, причем последняя дает большую экономию в объеме выборки. Однако иногда последовательная процедура с двумя порогами следует непосредственно из вида законов fa0(x), fa1(x). Этот случай часто встречается при распознавании образов.
Из формулы (3-52) следует еще одно очень важное соотношение
0≤α+β≥1. (3-58)
Действительно, так как аир - вероятности, то они должны быть положительными величинами и меньшими единицы, т. е.
0<α<1; 0<β<1. (3-59)
Далее из соотношения (3-55) следует, что
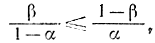
откуда
αβ≤αβ-α-β+1
Из этой формулы с учетом (3-59) следует формула (3-58), т. е. величины α и β могут задаваться из априорных соображений, но они должны удовлетворять соотношениям (3-58) и (3-59). Практически последовательная процедура считается законченной, если выборка перестала попадать в область, определяемую неравенством
В<Ln(x)<A.
Аналогично классической процедуре для нормального закона при известной дисперсии σ2 можно получить выражения для характеристик в явном виде. Последовательная процедура сводится к анализу величины ln с постоянным нижним и верхним порогами lnВ и lnA со случайным числом выборок. Для удобства переходим к величине
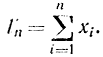
Для этой величины нижний и верхний пороги будут равны:
h0+kn, h1+kn, (3-60)
где
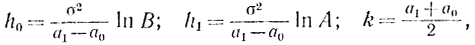
так как
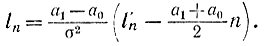
В этом случае интегральное уравнение (3-51) имеет точное решение
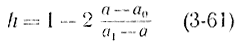
и операционная характеристика может быть рассчитана по следующей формуле:
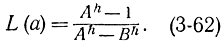
Средние числа испытаний определяются по формулам
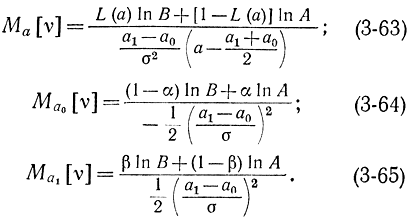
При а=a*=(а1+a0)/2, когда Mа*[ζ]=0 и
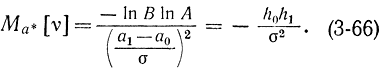
имеем:
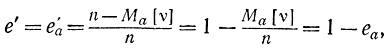
|
ПОИСК:
|
© Злыгостев А.С., 2001-2019
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'
При использовании материалов сайта активная ссылка обязательна:
http://informaticslib.ru/ 'Библиотека по информатике'