в) Сравнение последовательной и классической процедур

Произведено достаточно тщательное сравнение эффективности двух процедур, которое в основном показывает преимущества последовательной процедуры, так как в ней при одних и тех же а₀, a₁ α, β средние числа испытаний М_a0[ν] и M_a1[ν] меньше, чем фиксированное число испытаний n в соответствующей классической процедуре. Однако не при всех значениях параметра а среднее число испытаний в последовательной процедуре М_а[ν] меньше фиксированного числа испытаний в классической. Это можно утверждать только для значений а, близких к a=a₀ и a=a₁ Для сравнительной оценки эффективности последовательной процедуры вводится величина

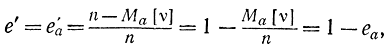
называемая эффективностью последовательного анализа. Для нормальной плотности f_a(х) при близких α и β, т. е. α≈β (так называемый случай симметричных порогов), и малых по величине, т. е. α≈β≈(0,05/0,1), получено, что е'_а=е_а≈0,5. Таким образом, при последовательной процедуре получается выигрыш в 2 раза. Однако в ряде случаев последовательный анализ дает и больший выигрыш. Но в некоторых случаях он менее эффективен, чем классический [Л. 34].

Когда последовательный анализ слишком затягивается, необходимо выносить решение о прекращении испытаний до выхода за пороги окончания процедур. В этом заключается проблема усеченного последовательного анализа, которая до сегодняшнего дня не получила удовлетворительного для инженерных задач решения.

Пример 3-6. Решение о наличии месторождения минерала X выносится на основании анализа n проб грунта в пределах исследуемой области. Известно, что разработка месторождения с содержанием минерала ρ≥2 г/м³ является нерентабельной, а при ρ≤1 г/м³ рентабельность разработки превышает среднее значение рентабельности рудных разработок.

Считается, что используемый метод измерений позволяет определить содержание минерала X в породе с ошибкой, распределенной нормально. Параметры распределения ошибки: m=4 г/м³ и σ=1 г/м³. Содержание минерала X во всех пробах в пределах предполагаемого месторождения постоянно, и отклонения в замерах происходят только из-за ошибок измерений. Требуется построить модели классической и последовательной проверок статистических гипотез для. случая, когда гипотеза простая. Основная трудность решения практических задач с помощью изложенных методов заключается в их сведении к проверке простой гипотезы. Поэтому первоначально сформулируем задачу следующим образом. Проблема сводится к задаче проверки гипотезы о значении математического ожидания случайной величины Y (измерение содержания минерала X) a=m+ρ, где m - математическое ожидание ошибки измерений; ρ - содержание минерала. На основании условий задачи легко выделить два значения а: а₀=5 г/м³ и а₁=6 г/м³, различение которых является необходимым. Таким образом, мы приходим к задаче проверки двух простых гипотез H→а=а₀ и H→а=а₁.

Необходимо построить критерий проверки этих гипотез, на оперативную характеристику которого наложены следующие ограничения:

где α и β - вероятности ошибок первого и второго рода. На основании предыдущего опыта принимаем α=β=0,05.

Для проверки гипотезы используем логарифм отношения (коэффициента) правдоподобия

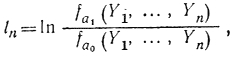
где Y_i - результат измерения содержания минерала X в i-й пробе 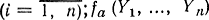- плотность распределения вероятности вектора наблюдений с параметром а.

Поскольку измерения можно считать независимыми, а их распределение нормальным, то

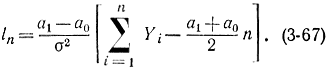
Рассмотрим две процедуры проверки гипотез H и H^-.

Классическая процедура (критерий Неймана - Пирсона). Согласно критерию Неймана - Пирсона решающее правило имеет вид:

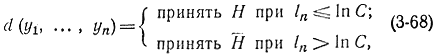
где С в общем случае определяется из условия

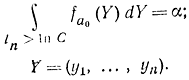
Величина вероятности ошибки второго рода является при этом функцией n и имеет минимально возможное (при данных α и n) значение.

В данном случае порог проще определять с помощью формул (3-48). Так как в нашем случае α и β заданы, то согласно соотношениям (3-48)

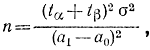
где t_α и t_β- квантили нормального распределения.

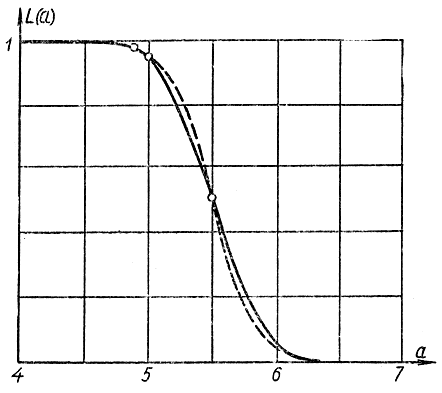
Рис. 3-4. Операционные характеристики для примера 3-6. __________ классическая процедура; ------ последовательная процедура

При α=β=0,05; а₀=5 г/м³; а₁=6 г/м³; σ=1 г/м³ получаем n=10,8 и принимаем n=11. В соответствии с формулами (3-48)

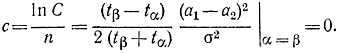
Поэтому решающее правило принимает вид:

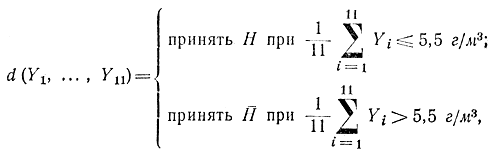
что непосредственно следует из формул (3-67) и (3-68) для конкретных значений α, β, а₀, а₁ и σ.

Операционная характеристика в соответствии с формулами (3-48) задается выражением

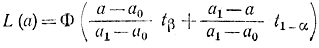
и показана на рис, 3-4.

Последовательная процедура (критерий Вальда). Согласно критерию Вальда решающее правило имеет вид:

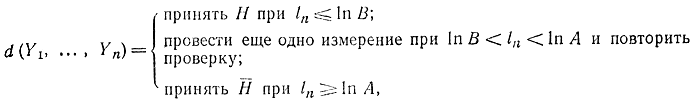
где

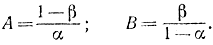
Операционная характеристика в соответствии с формулами (3-61), (3-62) задается выражением

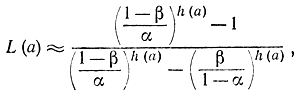
где

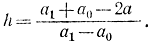
Для заданных значений α, β, а₁ и а₀

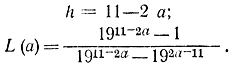
Операционная характеристика критерия Вальда показана на рис.3-4.

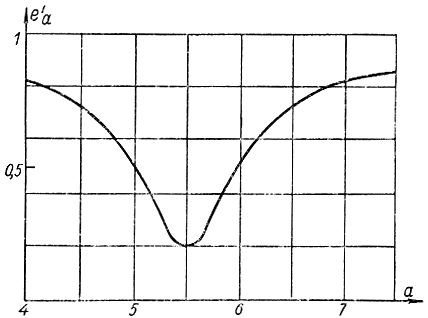
Рис. 3-5. Кривая эффективности последовательной процедуры для примера 3-6

Среднее число испытаний определяется формулой (3-63):

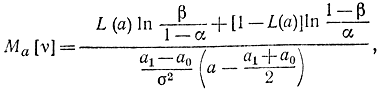
для конкретных значении параметров

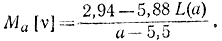
На рис. 3-5 показана кривая относительной эффективности последовательной процедуры

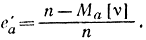
Анализ полученных результатов показывает:

1. операционные характеристики обеих процедур почти полностью совпадают и удовлетворяют поставленным условиям;
2. классическая процедура требует проведения 11 проб грунта для обеспечения заданной надежности решения;
3. последовательная процедура при любом содержании минерала X обладает эффективностью не менее е'_a= 0,21, т. е. среднее число проб не превосходит М_а[ν]≤(1-0,21)*11=8,65.