4-2. Получение последовательности случайных чисел

Очевидно, что успех и точность статистического моделирования зависят в основном от качества последовательности случайных чисел и выбора оптимального алгоритма моделирования.

Задача получения случайных чисел обычно разбивается на две. Вначале получают последовательность случайных чисел, имеющих равномерное распределение в интервале [0, 1]. Затем из нее получают последовательность случайных чисел, имеющих произвольный закон распределения. Один из способов такого преобразования состоит в использовании нелинейных преобразований. Пусть имеется случайная величина Х, функция распределения вероятности для которой

Если у является функцией х, т. е. y=F(х), то 0≤F(х)≤1 и поэтому 0 ≤y≤1. Таким образом, для получения последовательности случайных чисел, имеющих заданную функцию распределения F(х), необходимо каждое число y с выхода датчика случайных чисел (ДСЧ), который формирует числа с равномерным законом распределения в интервале [0, 1], подать на не-линейное устройство (аналоговое или цифровое), в котором реализуется функция, обратная F(х), т. е.

Полученная таким способом случайная величина X будет иметь функцию распределения F(x). Рассмотренная выше процедура может быть использована для графического способа получения случайных чисел, имеющих заданный закон распределения. Для этого на миллиметровой бумаге строится функция F(х) и вводится в рассмотрение другая случайная величина Y, которая связана со случайной величиной X соотношением (4-6) (рис. 4-2).

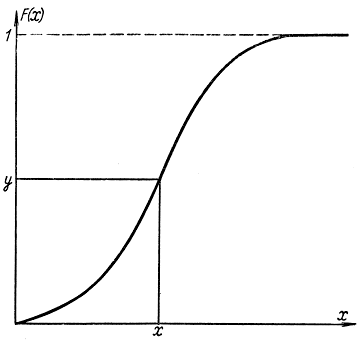
Рис. 4-2. Пояснения к процессу получения случайных чисел с любым законом распределения

Так как любая функция распределения монотонно неубывающая, то

Отсюда следует, что величина Y имеет равномерный закон распределения в интервале [0, 1], так как ее функция распределения равна самой величине

Плотность распределения вероятности для Y

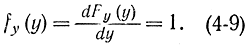
Для получения значения X берется число из таблиц случайных чисел, имеющих равномерное распределение, которое откладывается на оси ординат (рис. 4-2), и на оси абсцисс считывается соответствующее число X. Повторив неоднократно эту процедуру, получим набор случайных чисел, имеющих закон распределения F(х). Таким образом, основная проблема заключается в получении равномерно распределенных в интервале [0, 1] случайных чисел [Л. 38]. Один из методов, который используется при физическом способе получения случайных чисел для ЦВМ, состоит в формировании дискретной случайной величины, которая может принимать только два значения: 0 или 1 с вероятностями

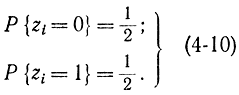
Далее будем рассматривать бесконечную последовательность z₁, z₂, ...,z_n как значения разрядов двоичного числа ξ* вида

Можно доказать, что случайная величина ξ*, заключенная в интервале [0, 1], имеет равномерный закон распределения

В цифровой вычислительной машине имеется конечное число разрядов k. Поэтому максимальное количество не совпадающих между собой чисел равно 2k. В связи с этим в машине можно реализовать дискретную совокупность случайных чисел, т. е. конечное множество чисел, имеющих равномерный закон распределения. Такое распределение называется квазиравномерным. Возможные значения реализации дискретного псевдослучайного числа 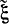в вычислительной машине с k разрядами будут иметь вид:

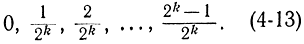
Вероятность каждого значения (4-13)равна 2^-k. Эти значения можно получить следующим образом:

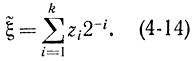
Случайная величина 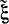имеет математическое ожидание

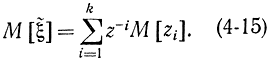
Учитывая, что

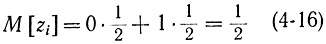
и выражение для конечной суммы геометрической прогрессии

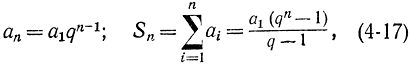
получаем:

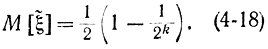
Аналогично можно определить дисперсию величины :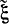

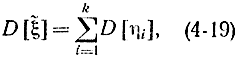
где

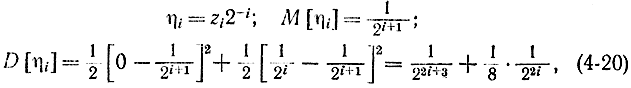
откуда

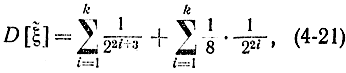
или, используя формулу (4-17), получаем:

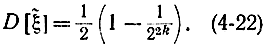
Согласно формуле (4-18) оценка 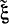величины ξ* получается смещенной при конечном k. Это смещение особенно сказывается при малом k. Поэтому вместо 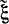вводят оценку

ξ= l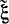 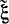(4-23)

где

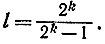
Очевидно, что случайная величина ξ в соответствии с соотношением (4-13) может принимать значения

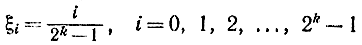
с вероятностью р = 1 /2^k.

Математическое ожидание и дисперсию величины ξ можно получить из соотношений (4-18) и (4-22), если учесть (4-23). Действительно,

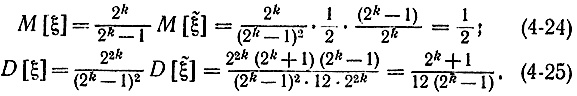
Отсюда получаем выражение для среднеквадратичного значения в виде

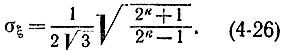
Напомним, что для равномерно распределенной в интервале [0,-1] величины х имеем:

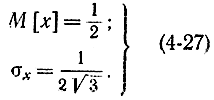
Из формулы (4-26) следует, что при k→∞ среднеквадратичное отклонение а квазиравномерной совокупности стремится к 1/2(3)^1/2. Ниже приведены значения отношения среднеквадратичных значений двух величин ξ и η в зависимости от числа разрядов [Л. 38], причем величина η имеет равномерное распределение в интервале [0, 1] (табл. 4-1).

Таблица 4-1

Из табл. 4-1 видно, что уже при k410 различие в дисперсиях несущественно.

На основании вышеизложенного задача получения совокупности квазиравномерных чисел сводится к получению последовательности независимых случайных величин z_i(i=1, 2, ...,k), каждая из которых принимает значение 0 или 1 с вероятностью 1/2. Различают два способа получения совокупности этих величин: физический способ генерирования и алгоритмическое получение так называемых псевдослучайных чисел. В первом случае требуется специальная электронная приставка к ЦВМ, во втором случае загружаются блоки машины.

При физическом генерировании чаще всего используются радиоактивные источники или шумящие электронные устройства. В первом случае радиоактивные частицы, излучаемые источником, поступают на счетчик частиц. Если показание счетчика четное, то z_i= 1, если нечетное, то z_i= 0. Определим вероятность того, что z_i=1. Число частиц к, которое испускается за время Δt, подчиняется закону Пуассона:

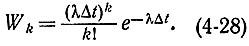
Вероятность четного числа частиц

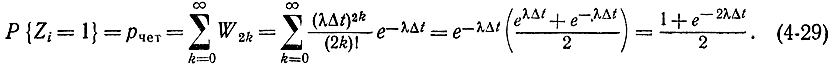
Таким образом, при больших ХМ вероятность Р{Z_i=1} близка к 1/2.

Второй способ получения случайных чисел z_i более удобен и связан с собственными шумами электронных ламп. При усилении этих шумов получается напряжение u(t), которое является случайным процессом. Если брать его значения, достаточно далеко отстоящие друг от друга, так чтобы они были не коррелированы, то величины u(t_i) образуют последовательность независимых случайных величин. Обычно выбирают уровень отсечки а и полагают

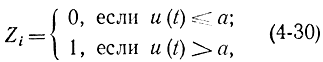
причем уровень а следует выбрать так, чтобы

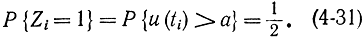
Простая логика (4-47) обычно не обеспечивает хорошего выполнения условия (4-48).Поэтому применяют более сложную логику образования чисел Z_i. В первом варианте используют два соседних значения u(t_i) и u(t_i+1), и величина Z_i строится по такому правилу:

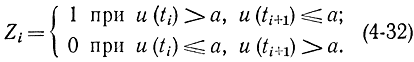
Если пара u(t_i)-а и u(t_i+1)-а одного знака, то берется следующая пара. Требуется определить вероятность при заданной логике. Будем считать, что Р {u(t_i)>а)=W и постоянная для всех t_i. Тогда вероятность события А₁={u(t_i)>а, u(t_i+1)≤а} равна по формуле полной вероятности бесконечной сумме вероятностей произведений событий A₁H_ν. Здесь H_ν - это вероятность того, что ν раз появилась пара одинакового знака

Поэтому вероятность события A₁H_ν

Это - вероятность того, что после ν пар вида (4-33) появилось событие Ах. Оно может появиться сразу с вероятностью W(1 - W), оно может появиться и после одной пары вида (4-33) с вероятностью

и т. д. В результате

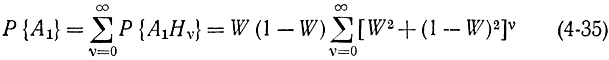
или

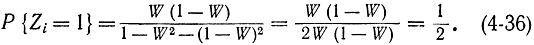
Отсюда следует, что если W=const, то логика обеспечивает хорошую последовательность случайных чисел. Второй способ формирования чисел Z_i состоит в следующем:

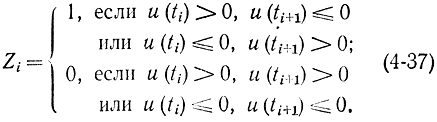
Пусть

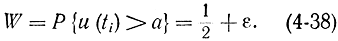
Тогда

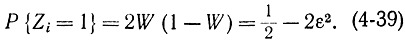
Чем меньше ε, тем ближе вероятность Р{Z_i=1} к величине 1/2.

Для получения случайных чисел алгоритмическим путем с помощью специальных программ на вычислительной машине разработано большое количество методов. Так как на ЦВМ невозможно получить идеальную последовательность случайных чисел хотя бы потому, что на ней можно набрать конечное множество чисел, такие последовательности называются псевдослучайными. На самом деле повторяемость или периодичность в последовательности псевдослучайных чисел на-ступает значительно раньше и обусловливается спецификой алгоритма получения случайных чисел. Точные аналитические методы определения периодичности, как правило, отсутствуют, и величина периода последовательности псевдослучайных чисел определяется экспериментально на ЦВМ. Большинство алгоритмов получается эвристически и уточняется в процессе экспериментальной проверки. Рассмотрение начнем с так называемого метода усечений [Л. 42]. Пусть задана произвольная случайная величина u, изменяющаяся в интервале [0, 11, т. е. 0≤u≤1. Образуем из нее другую случайную величину

где u[mod 2^-n] используется для определения операции получения остатка от деления числа и на 2^-n. Можно доказать, что величины u_n в пределе при n→∞ имеют равномерное распределение в интервале [0, 1].

По существу с помощью формулы (4-40) осуществляется усечение исходного числа со стороны старших разрядов. При оставлении далеких младших разрядов естественно исключается закономерность в числах и они более приближаются к случайным. Покажем это на примере.

Пример 4-1. Пусть

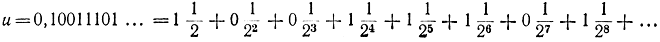
Выберем для простоты n=4. Тогда {u mod 2^-4}=0,1101...

Из рассмотренного свойства ясно, что существует большое количество алгоритмов получения псевдослучайных чисел. При этом после операции усечения со стороны младших разрядов применяется стандартная процедура нормализации числа в цифровой вычислительной машине. Так, если усеченное слева число не умещается по длине в машине, то производится усечение числа справа. Наиболее показателен метод Н. М. Соболя, используемый в ЦВМ "Стрела" [Л. 43]. Схема расположения разрядов в ячейке машины "Стрела" представлена на рис. 4-3. Это - трехадресная машина с плавающей запятой, работающая с двоичными числами в нормализованной форме:

где М_х - мантисса числа, удовлетворяющая условию нормализации 0,5≤М<1; р - порядок числа. В j-м разряде может стоять нуль или единица, т. е. ε_j=0 или 1. Тогда

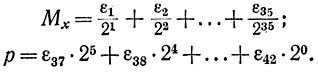
Условие нормализации означает, что ε₁=1. Знаки числа и порядка изображаются: плюс - нулем, минус - единицей. Число α_k+1 получается из числа α_k с помощью следующей рекуррентной процедуры, состоящей из трех операций:

1. умножения α_k на большую константу К=10¹⁷;
2. сдвига изображения числа 10¹⁷ в сетке машины на 7 разрядов влево [т. е. в формуле (4-40) n=7]. При этом первые семь разрядов произведения пропадают и в разрядах с 3-го по 42-й оказываются нули;
3. определения абсолютной величины полученного числа, при которой происходит нормализация числа.

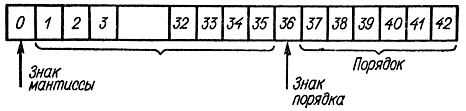
Рис. 4-3. Схема расположения разрядов в ячейке машины 'Стрела'

При а₀=1 можно таким способом получить 80 ООО различных чисел α_k, после чего в последовательности чисел возникает периодичность. Вероятность вырождения чисел, т. е. обращения α_k+1, а следовательно, и всех последующих чисел в нуль, очень мала. Действительно, α_k+1 обратится в 0 только тогда, когда

так как в противном случае в порядке произведения окажутся цифры, отличные от нуля, и при сдвиге они попадут в мантиссу числа α_k+1. Но условие (4-41) можно переписать в виде

т. е. для вырождения число α_k должно попасть в очень узкий интервал значений. Отсюда следует, что чем больше число K, тем меньше вероятность вырождения.

При проверке качества псевдослучайных чисел прежде всего интересуются длиной отрезка апериодичности и длиной периода (рис. 4-4). Под длиной отрезка апериодичности L понимается совокупность последовательно полученных случайных чисел α₁,α₂,...,α_L таких, что α_i≠α_j при 1≤i≤L, 1≤ j≤L, i≠j, но α_L+1 равно одному из α_k(1≤k≤L).

Под длиной периода последовательности псевдослучайных чисел понимается Т=L-i+1. Начиная с некоторого номера i числа будут периодически повторяться с этий периодом (рис. 4-4).

Рис. 4-4. Поведение последовательности псевдослучайных чисел

Как правило, эти два параметра (длины апериодичности и периода) определяются экспериментально. Так, для рассмотренной выше программы Н. М. Соболя L=80 000, а длина периода α=50 000. Качество совпадения закона распределения случайных чисел с равномерным законом проверяется с помощью критериев согласия, рассмотренных в предыдущих разделах.