4-3. Точность метода Монте-Карло

Метод Монте-Карло применяется там, где не требуется высокой точности. Например, если определяют вероятность поражения мишени при стрельбе, то разница между p₁=0,8 и p₂=0,805 несущественна. Обычно считается, что метод Монте-Карло позволяет получить точность примерно 0,01-0,05 максимального значения определяемой величины.

Получим некоторые рабочие формулы [Л. 38]. Определим по методу Монте-Карло вероятность пребывания системы в некотором состоянии. Эта вероятность оценивается отношением

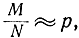
где М - число пребываний системы в этом состоянии в результате N моделирований. Учитывая выражение для дисперсии величины M/N

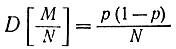
и неравенство Чебышева

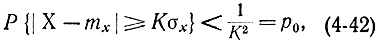
напишем

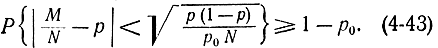
Величина

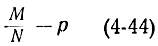
есть не что иное, как ошибка моделирования по методу Монте-Карло. С помощью формулы (4-42) можно написать следующую формулу для величины (4-43):

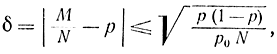
или

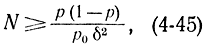
где p₀ - вероятность невыполнения этой оценки. Из соотношения (4-41) следует, что погрешность метода Монте-Карло

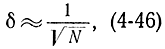
следовательно, для уменьшения погрешности δ в 10 раз число реализаций необходимо увеличить в 100 раз. Этим обстоятельством и обусловливается невысокая точность моделирования по методу Монте-Карло.

Аналогично с помощью частоты М/N может быть получена оценка математического ожидания m_x некоторой случайной величины X. Ошибка этой оценки

находится с помощью соотношения

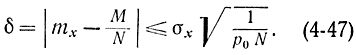
Отсюда видно, что ошибка моделирования находится в квадратичной зависимости от числа реализаций, т. е.

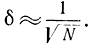
Пример 4-2. Допустим, что определяется математическое ожидание ошибки х поражения мишени. Процесс стрельбы и поражения моделируется на ЦВМ по методу Монте-Карло. Требуется точность моделирования δ=0,1 м с вероятностью р=1-p₀= 0,9 при заданной дисперсии σ_x=1 м. Необходимо определить количество моделирований N. По формуле (4-66) получаем:

При таком количестве реализаций обеспечивается δ=0,1 м с вероятностью р=0,9.

Можно получить еще более удобные выражения, чем (4-45) и (4-47), если учесть, что оценка величины р_х подчиняется нормальному распределению вероятности. Известно правило За (см. гл. 1), в соответствии с которым вероятность превышения в три раза среднеквадратичного значения отклонения от математического ожидания меньше 0,003, т. е.

Тогда вместо формулы (4-45) имеем:

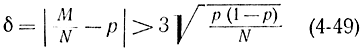
или

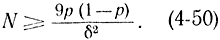
Отсюда может создаться мнение, что при малых р≈0 и больших р≈1 требуется малое число испытаний, но на самом деле это неверно. Как будет показано ниже, для этих двух случаев не удовлетворяются условия Ляпунова предельной теоремы и нельзя использовать нормальный закон распределения. Аналогичным образом для больших р (например, р=0,996) δ следует брать тоже малой (δ=0,005). Поэтому отношение р(1-р)/δ² будет большим.

Аналогично вместо формулы (4-47) можно написать:

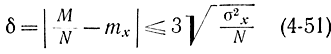
или

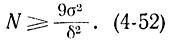
Из формул (4-50) и (4-51) видна обратная квадратичная зависимость между точностью вычисления δ и числом реализаций N, что позволяет пол учить'высокую точность метода Монте-Карло с помощью цифровых или аналоговых вычислительных машин. Если ввести понятие доверительной вероятности β получения параметров по методу Монте-Карло и применить положения, полученные в разделе теории оценок, можно вывести ряд полезных формул для точности статистического моделирования. Пользуясь неравенством-Чебышева и учитывая, что средне-квадратичное значение величины X при N моделированиях определяется по формуле 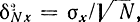, получаем:

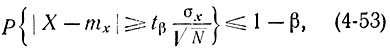
где

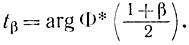
Тогда для ошибки с доверительной вероятностью β можно написать:

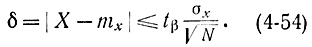
Поэтому

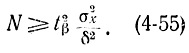
Эта формула дает выражение для числа испытаний, при которых обеспечивается требуемая точность δ при заданной доверительной вероятности β и исходной дисперсии σ²_x исследуемой величины X.

Для случая определения вероятности имеем:

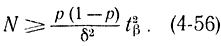
Пример 4-3. Для условий примера 4-2 найдем необходимое число реализаций N для определения вероятности поражения мишени с заданной точностью δ=0,01, Доверительная вероятность задается равной β=0,99. Считается, что оценка вероятности р подчиняется нормальному закону, т. е. величина р - не малая и не большая, и число реализаций большое.

Используя формулу (4-55), получаем:

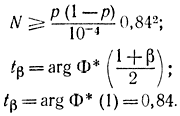
В практических расчетах можно считать приближенно, что для не очень больших и не очень малых р произведение

В районе точки р=0,5 это произведение изменяется слабо. Поэтому

Получим важные для практики формулы, введя вместо абсолютной ошибки δ относительную ошибку

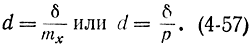
Учитывая соотношение (4-54), получаем:

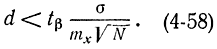
Если ввести в рассмотрение максимально допустимое значение относительной ошибки d_макс, то вместо формулы (4-55) можно написать:

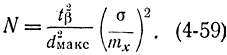
Применительно к определению вероятности формулы (4-53) и (4-59) запишутся в виде

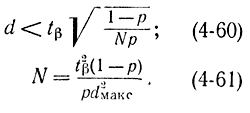
Пример 4-4. Для условия примера 4-3 определим необходимое число испытаний для получения максимальной относительной ошибки d_макс= 0,01 при условии, что р=0,5.

Подставив цифровые данные в формулу (4-61), получим:

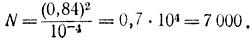
Отсюда следует, что получение относительной точности порядка 1% при доверительной вероятности β=0,99 по методу Монте-Карло сопряжено с большим количеством испытаний.

Аналогичные оценки точности моделирования δ= |-σ²| можно получить для дисперсии. Мы уже отмечали, что оценка дисперсии

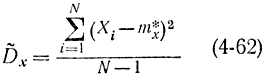
асимптотически распределена нормально. Вспомним формулу для оценки дисперсии

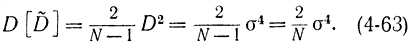
Применив неравенство Чебышева к нормально распределенной величине (4-62) и учитывая, что

М[]=D=σ²,

получим:

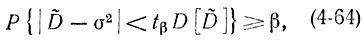
откуда

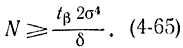
Статистическое моделирование с целью определения малых значений вероятности затруднительно, так как N обратно пропорционально р [формула (4-61)]. Поэтому задачу необходимо преобразовать. Можно показать, что при малых р частота события р*=M/N не подчиняется нормальному закону распределения и формулы для оценки точности моделирования по методу Монте-Карло, основанные на ЦПТ, не справедливы. Известно, что величина М подчиняется биномиальному закону распределения. Если при устремлении числа опытов N к ∞ одновременно р→0, так что

то из биномиального закона получается закон Пуассона с параметром a [Л. 21]. Покажем, что в этом случае при малых р не удовлетворяются условия центральной предельной теоремы Ляпунова. Действительно,

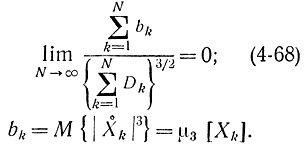
Полагая, что третьи моменты и дисперсии замеров одинаковы

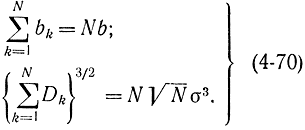
Поэтому формула (4-68) может быть записана в виде

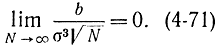
В соответствии с формулами (4-69) и (4-70), а также учитывая, что для биномиального распределения 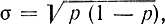, получаем:

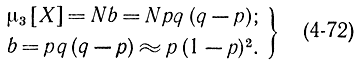
Поэтому

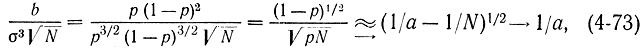
т. e. условия предельной теоремы не выполняются.

Очевидно, что все изложенное здесь остается в силе, если мало q=1-р и 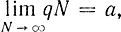, так как во все формулы р и q входят симметрично. Поэтому как при малых p, так и при p, близких к 1, закон распределения величины p* может не стремиться к нормальному, и формулы, связанные с предположением нормальности, не справедливы. Формулами, не связанными с нормальным распределением (4-42) - (4-47), пользоваться можно, но следует иметь в виду, что они дают несколько завышенный (примерно на 30%) результат.