4-4. Примеры расчетов по методу Монте-Карло

Рассмотрим несколько примеров на применение метода Монте- Карло.

Определение площадей и объемов. Остановимся вначале на принципе определения площадей. Допустим, требуется определить интеграл

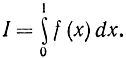
Если пределы произвольные, то изменением масштабов по осям абсцисс и ординат всегда можно добиться, чтобы величина х изменялась в пределах [0, 1], а функция f(x) - в пределах от 0 до 1 при 0≤x≤1 (рис. 4-5). Требуется определить площадь, ограниченную кривой f(x), осью абсцисс и прямыми х=0 и х=1. Для этого необходимо иметь два независимых датчика случайных чисел (ДСЧ), которые выдают две последовательности случайных чисел х и y равномерно распределенных в интервале [О, 1]. Пусть в квадрат случайно попала точка (ξ,η). Вероятность попадания точки под кривую равна площади, т. е. интегралу.

Берем пару первых, случайных величин ξ,η и проверяем условие

Если оно выполнено, то точка попала под кривую.

Проделав этот эксперимент N раз и определив, сколько раз точка оказывалась под кривой М, получим, что

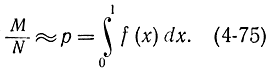
Тем самым задача решена.

однако использовать способ, требующий для вычислений один датчик случайных чисел [Л. 43]. При этом заметим, что интеграл

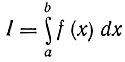
можно записать в виде

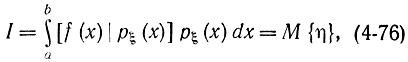
где η=f(ξ)/p_ξ(ξ) - некоторая вспомогательная случайная величина, зависящая от случайной величины ξ, которая задается таблицей или получается с помощью ДСЧ.

Слева в формуле (4-76) выражение равно математическому ожиданию случайной величины η. Поэтому приближенно интеграл можно вычислять по формуле

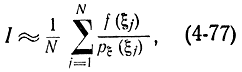
где ξ_j(j=1, 2,..., N) - случайно выбранные точки; N - число испытаний по методу Монте-Карло.

Пример 4-5. Определим [Л. 43] значение интеграла

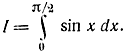
Допустим, что числа ξ_j имеют равномерный закон распределения вероятности на интервале [0, π/2]

В соответствии с методикой (см. § 4-2) получения случайных чисел с заданным законом распределения р_ξ(х) из случайной величины γ, имеющей равномерный закон распределения в интервале [0,1] необходимо аналитически или графически определить ξ, пользуясь уравнением

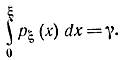
Получаем:

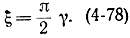
Эта процедура увеличивает интервал [0,1] до [0, π/2]. В качестве случайных чисел используем случайно выбранные тройки чисел из последовательности случайных чисел, помещенных в приложении 6. Эта таблица содержит 400 случайных чисел, которые имеют следующий закон распределения:

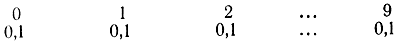
Можно убедиться, что в этой последовательности из 400 чисел каждая из цифр 0, 1, ..., 9 встречается в среднем примерно 10%. Для удобства все цифры сгруппированы по пятеркам, но надо всегда иметь в виду, что имеется последовательность, состоящая из 400 цифр вида 8 651 569 186 ... Эти числа можно получить с помощью следующего физического эксперимента: на десяти одинаковых бумажках пишут цифры 0, 1, ..., 9, вытаскивают бумажку наугад, записывают номер и возвращают на место. Такой опыт проделывают 400 раз.

Учитывая, что в данном случае f(х)=sin х и принимая во внимание соотношение (4-78), формулу (4-77) перепишем в виде

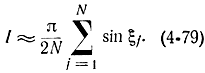
Полагаем N=10, выбираем случайным образом десять троек случайных цифр из приложения 6 и умножаем их на 0,001. Результаты расчетов сводим в табл. 4-2.

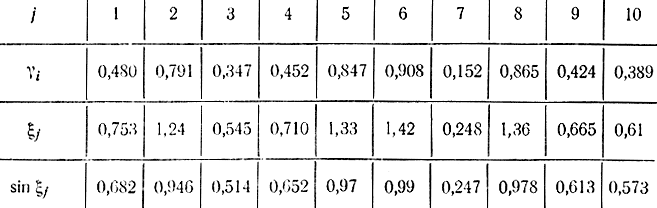
Таблица 4-2

Подставив эти данные в формулу (4-78), получим I=1,12 вместо точного значения I=1. Таким образом, точность будет равна 12%.

Аналогичная методика может быть применена для взятия кратных интегралов. При кратности n>3 метод Монте-Карло экономичнее по времени счета, чем классический численный метод кубатур. В табл. 4-3 приведены сравнительные данные [Л. 38] времени счета для одних и тех же задач, выполненных этими двумя методами (быстродействие машины 5 000 операций!сек).

Таблица 4-3

Моделирование систем массового обслуживания. В кибернетике для описания работы сложных систем широко применяются модели теории массового обслуживания. К примеру, работу телефонного узла города или парикмахерских можно описать с помощью набора систем массового обслуживания, соединенных определенным образом, или сети массового обслуживания. Заявки, поступающие на телефонную станцию, или клиенты, приходящие в парикмахерскую, изображаются в виде случайных точек на оси времени, расположение которых определяется законом распределения вероятности. Каждый мастер в парикмахерской или телефонная линия связи представляется отдельной системой массового обслуживания, которая характеризуется случайным временем обслуживания с известным законом распределения вероятности. В качестве исходных данных должны быть также заданы законы распределения времени ожидания заявок в очереди перед обслуживанием (дисциплина очереди).

Сложные системы массового обслуживания аналитически не рассчитываются, и для определения их параметров прибегают к статистическому моделированию. На ЦВМ в виде числа набирается время поступления заявки. По существу с помощью программы псевдослучайных чисел последовательно набираются интервалы между заявками в соответствии с заданным законом распределения этих интервалов. Каждая заявка-число проходит все стадии обслуживания, т. е. задерживается на случайные времена обслуживания и появляется на выходе модели. Для получения статистических характеристик в алгоритме решения задачи предусмотрены специальные блоки подсчета среднего времени ожидания в очереди и пр.

На рис. 4-6 приведена схема моделирования одноканальной системы массового обслуживания с отказами [Л. 39]. В этой схеме использованы четыре типа блоков:

1. формирователи заданного набора случайных чисел, представляющих временные интервалы (1, 4, 9);
2. операторы проверки условий (обозначены кружочками). Если условие выполняется, то управление от предыдущего оператора передается к следующему, обозначенному цифрой "1", если нет - то к оператору с цифрой "0";
3. блоки, вычисляющие момент начала обслуживания (7, 8);
4. прочие вычислительные блоки.

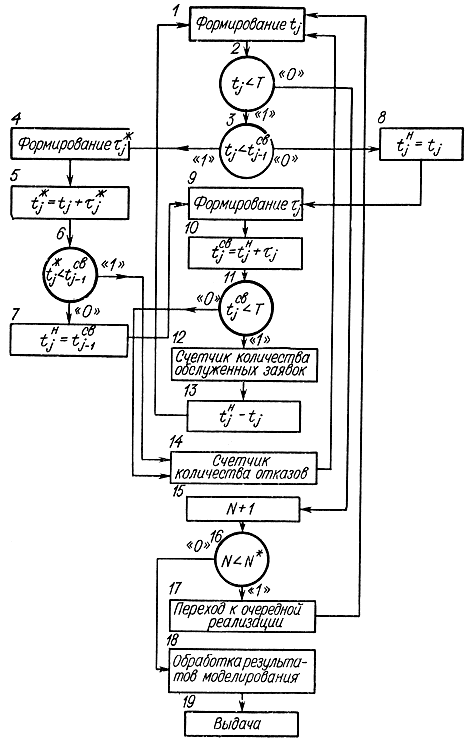
Рис. 4-6. Схема моделирования на ЦВМ одноканальной системы массового обслуживания

В блоке 1 формируются случайные числа, которые имитируют однородный поток событий в соответствии с заданным законом распределения. Случайное число, получившееся в блоке 1, поступает в блок проверки условия t_j<Т, где Т - время, отведенное на весь процесс моделирования всех заявок. При удовлетворении условий, задаваемых блоком 2, число-заявка поступает на блок 3 проверки условия t_j<t_j^СВ- свободен ли канал обслуживания. Если условие удовлетворяется, канал не свободен, то управление передается к блоку 4, где формируется случайное число, равное времени ожидания τ_j^жj-й заявки. Оператор 5 вычисляет момент предполагаемого поступления j-й заявки t_j^ж=t_j+τ_j^ж в соответствии с заданной дисциплиной очереди. Блок-оператор 6 проверяет, может ли данная заявка быть обслужена с учетом времени ожидания и обслуживания. Для этого в блоке сравниваются предполагаемое время начала обслуживания j-й заявки t_j^ж и окончания обслуживания предыдущей заявки t_j-1^СВ. Если условие оператора 6 выполняется, то j-я заявка не может быть обслужена и получает отказ, управление передается блоку 14 подсчета числа отказов. Если это условие не выполняется, то управление передается по стрелке "О" к блоку 7 вычисления момента начала обслуживания. Число с выхода этого блока поступает на блок 9, формирующий время обслуживания j-й заявки. На этот же блок поступает число с блока 8, формирующего начало обслуживания t_j^н=t_jj-й заявки, если в момент прихода канал свободен. Оператор 10 формирует момент освобождения канала от j-й заявки. Это время снова поступает на блок 11 проверки условия t_j^СВ≤T. Если канал освободился позже этого времени, управление поступает на блок 14 подсчета отказов. Если условие удовлетворяется, управление поступает на блок 12 подсчета числа обслуженных заявок. Оператор 13 служит для вычисления времени пребывания заявок в системе t_j^H-t_j. От это го блока управление передается к блоку 1 для формирования следующей заявки, т. е. канал освобожден Если условие блока 11 не выполняется, данная заявка подсчитывается как получившая отказ и эта команда служит для начала моделирования следующей заявки. Наконец, если условие оператора 2 не выполняется, к числу реализаций добавляется единица (блок 15), и, если это число не превысило заданное N* (блок 16), дается команда на переход к следующей реализации (блок 17).

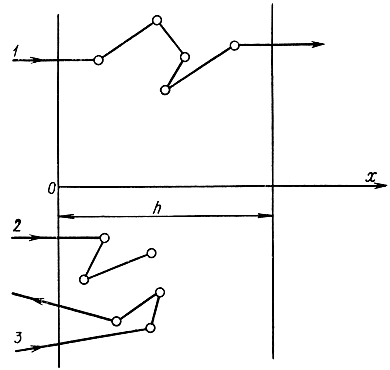
Рис. 4-7. Возможности случаи при прохождении нейтронов через пластинку. 1 - прохождение сквозь пластину; 2 - поглощение; 3 - отражение

Расчет прохождения нейтронов сквозь пластинку. Наибольшее распространение метод Монте-Карло получил в нейтронной физике. Ниже будет рассмотрена упрощенная задача о прохождении нейтронов через пластинку [Л. 43]. На однородную бесконечную пластинку толщиной h падает под углом 90° поток нейтронов с энергией Е₀. При прохождении нейтронов через вещество, из которого состоит пластинка, происходят столкновения с атомами этого вещества. Для простоты предполагается, что возможны два вида удара: идеально упругий и неупругий, когда нейтрон поглощается. В первом случае считается, что нейтрон рассеивается равновероятно в любом направлении и энергия его сохраняется. Могут представиться три случая, изображенные на рис. 4-7. Ставится задача определить вероятности этих событий: р⁺, p°, p^-- прохождения, поглощения и отражения нейтрона. В нейтронной физике вводятся характеристики взаимодействия нейтронов с веществом, называемые сечениями поглощения Σ_c и рассеяния Σ_s. Эти величины определяют вероятность поглощения нейтрона Σ_c/Σ и вероятность его рассеяния Σ_s/Σ при столкновении с атомами вещества. Здесь и называется полным сечением. Считается, что длина свободного пробега нейтрона λ (расстояние от столкновения до Столкновения) является положительной случайной величиной с экспоненциальной плотностью распределения вероятности

Математическое ожидание свободного пробега к обратно пропорционально полному сечению:

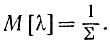
Для получения случайной величины λ из случайной величины γ, имеющей равномерный закон распределения, необходимо осуществить операцию разыгрывания в соответствии с формулой

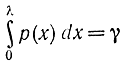
или

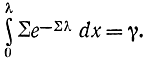
После взятия интеграла в левой части получим окончательно формулу для разыгрывания в виде

Так как величина у положительная и равномерно распределенная, то формулу (4-80) можно переписать:

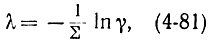
имея в виду, что закон распределения величины 1 - γ также равномерный в интервале [0, 1].

Теперь необходимо выяснить, как выбирать направление нейтрона после удара. Оно может быть определено углом φ между осью ОХ и направлением движения нейтрона. Покажем, что условие равновероятности любого направления эквивалентно равномерности распределения величины μ=cos φ в интервале [-1,1].

Переходя к пространственной задаче, условие равновероятности можно сформулировать как требование того, что точка А на сфере единичного радиуса с центром в точке столкновения нейтрона с атомом окажется равновероятным образом в любом элементе поверхности сферы dS с вероятностью dS/4π. В данном случае точка А может рассматриваться как точка пересечения траектории нейтрона после столкновения. Выбираем сферические координаты (φ, ψ) с полярной осью ОХ, причем О≤φ≤π, О≤ψ≤2π. Очевидно, что dS=sinφdφdψ. Используя это соотношение и условие независимости координат φ и ψ напишем для плотности распределения точки А на сфере с координатами φ и ψ выражение:

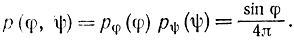
Интегрируя это выражение по φ от 0 до 2π и учитывая, что

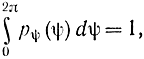
получаем:

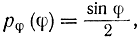
откуда

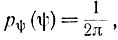
т. е. величина φ имеет равномерный закон распределения в интервале [О, 2π], и для разыгрывания ψ следует использовать формулу

Соответствующая формула разыгрывания для величины φ получается из соотношения

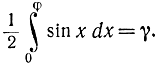
Следовательно,

Из (4-82) следует, что при изменении γ в интервале [0, 1] μ изменяется в интервале [-1, 1] или

Формула (4-83) получается из (4-82) заменой γ на 1-γ, а обе эти величины имеют одинаковое распределение. Таким образом, для разыгрывания угла ψ следует использовать формулу (4-83), примененную для разыгрывания cosφ.

Перейдем к построению схемы моделирования (рис. 4-8). Обозначим абсциссы двух последовательных столкновений нейтрона с атомами x_k и x_k+1, номер траектории j(j=1,..., N), номер столкновения k. Разыграем длину свободного пробега после k-то столкновения (блок 4) по формуле

и вычислим абсциссу следующего столкновения (блок 3):

где μ_k=cosφ_k - направление движения нейтрона после k-го столкновения. Далее проверим условие прохождения нейтрона сквозь пластинку (блок 6)

При удовлетворении этого условия (выход "1") расчет траектории заканчивается и добавляется единица к счетчику прошедших частиц (блок 7). Если это условие не выполняется (выход "О"), то следует проверить k+1 столкновений на отражение блок 8). Для этого выбираем очередное значение γ и проверяем условие поглощения (блок 10)

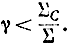
При выполнении этого условия расчет траектории заканчивается и добавляется единица к счетчику поглощенных частиц (блок 11). В противном случае электрон испытал рассеяние в точке x_k+1 и разыгрывается новое направление скорости движения нейтрона (блок 12) по формуле

По существу для расчета k-то шага требуются три значения γ. Начальные значения для всех траекторий можно выбрать следующие:

В результате N-кратного расчета траекторий определяются числа нейтронов, прошедших сквозь пластинку N⁺, отразившихся от нее N^- и поглощенных веществом пластинки N⁰. Соответственно вероятности определяются по формулам:

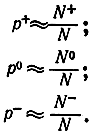
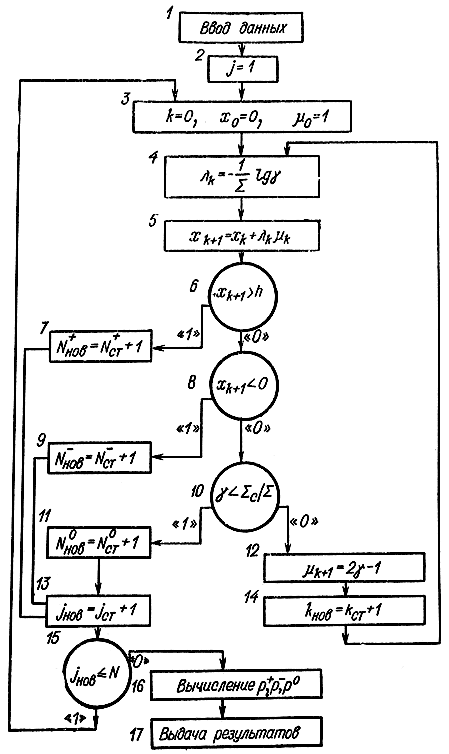
Рис. 4-8. Схема моделирования на ЦВМ процесса прохождения частиц через пластинку