5-1. Примеры сигналов. Модели сигнала

Рассмотрим импульсный сигнал, отраженный от цели в импульсной радиолокации [Л. 46]. Радиолокатор периодически, с периодом T, посылает импульсы определенной формы в сторону цели, которые, отразившись, возвращаются на вход приемника (рис. 5-2, а). Задержка τ³ этих импульсов относительно излученных пропорциональна дальности до цели D. Построение математической модели реального физического сигнала заключается в замене его амплитудно-модулированным сигналом (рис. 5-2, б), состоящим из последовательности δ-импульсов, амплитуда которых равна дискретным значениям дальности до цели или времени задержки отраженных импульсов относительно излученных.

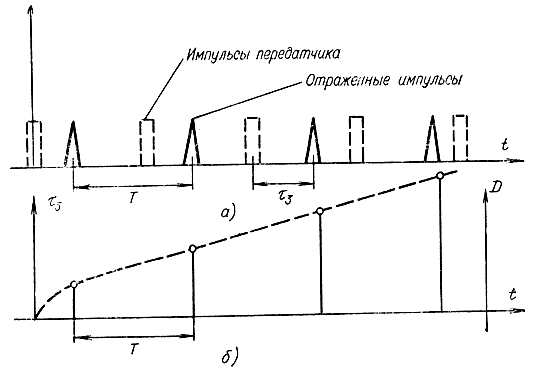
Рис. 5-2. Дискретный по времени радиолокационный сигнал

Математические модели в зависимости от природы сигналов делятся на детерминированные и случайные. Чаще всего в теории информации, как и в кибернетике, используются случайные модели сигналов, которые могут быть стационарными и нестационарными, марковскими и не марковскими, непрерывными и дискретными. Дискретные сигналы различаются по времени и амплитуде и в соответствии с этим их называют квантованными по времени или амплитуде. При квантовании по времени берутся значения непрерывного сигнала в дискретные моменты времени. Интервал квантования по времени равен периоду излучения импульсов передатчиком. В общем случае интервалы между моментами времени могут не быть равными [Л. 47, 48].

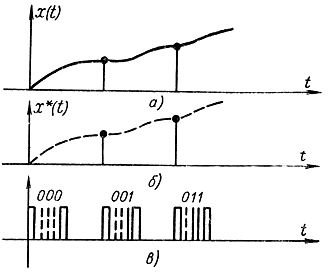
Рис. 4-3. Дискретный по времени сигнал при цифровой системе передачи. а - исходный непрерывный сигнал; б - соответствующий дискретный сигнал; в - последовательность кодированных импульсов

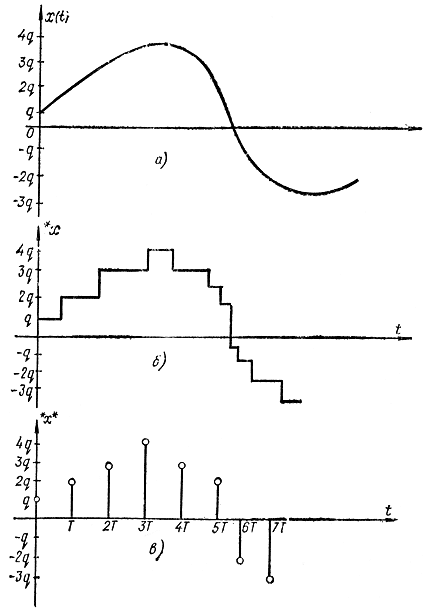
Рис. 5-4. Процесс квантования непрерывного сигнала по времени и амплитуде. а - исходный непрерывный сигнал; б - квантование по амплитуде; в - квантование по амплитуде и времени

В качестве примера сигнала, квантованного по амплитуде и времени, рассмотрим сигнал, закодированный двоичным кодом, который часто применяется для передачи сообщения на расстояние (рис. 5-3) при цифровой системе передачи данных. На рис. 5-3, а представлен непрерывный сигнал, на рис. 5-3, б - тот же сигнал, но квантованный по времени, на рис. 5-3, в каждое из этих дискретных значений сигнала представлено в виде последовательности импульсов, закодированных двоичным кодом. Каждая кодовая комбинация отделяется от другой маркерным импульсом. Естественно, что с помощью конечного числа двоичных разрядов (в данном случае их три) нельзя представить точно дискретное значение. Прежде чем сигнал (рис. 5-4, а) закодировать двоичным кодом, его необходимо проквантовать с уровнем квантования, определяемым величиной младшего двоичного разряда. На рис. 5-4, б представлен сигнал, дискретный по амплитуде. Если его пропустить через ключ, который замыкается с периодом Т, то получится сигнал, квантованный по амплитуде и времени (рис. 5-4, в). Для получения из непрерывного сигнала x(t) сигнала *х(t), квантованного по амплитуде, необходимо пропустить его через нелинейный элемент, характеристика которого представлена на рис. 5-5. Условное изображение элемента квантования ЭК показано на рис. 5-6, а, квантователя по времени в виде ключа — на рис. 5-6, б. При пропускании непрерывного сигнала х(t) (рис. 5-7, а) через такой элемент на выходе получается дискретный (квантованный по времени) сигнал х*(t), представленный на рис. 5-7, б. Если непрерывный сигнал x(t) пропустить через последовательно соединенные ключ и элемент квантования по уровню (рис. 5-6, в)у то на выходе получим сигнал *х*(t), квантованный по . времени и амплитуде, причем очевидно, что ключ и элемент квантования можно поменять местами (рис. 5-6, г).

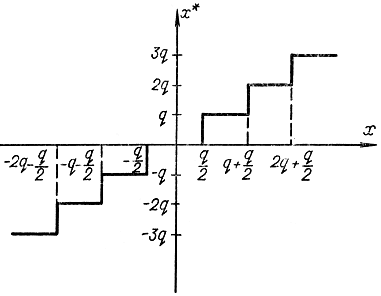
Рис. 5-5. Характеристика квантования

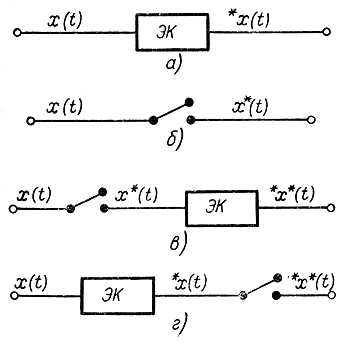
Рис. 5-6. Квантования сигнала по амплитуде и времени. а - по амплитуде; б - по времени; в - по времени и амплитуде; г - по амплитуде и времени

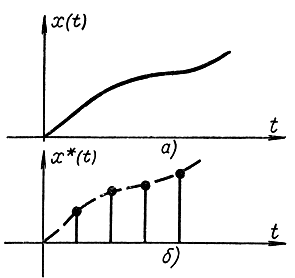
Рис. 5-7. Непрерывный (а) и дискретный (б) по времени сигналы