5-2. Частотные свойства сигнала (теорема Котельникова)

Следует заметить, что с точки зрения кибернетики при получении информации человек с помощью приборов может воспринимать только квантованный по времени и амплитуде сигнал. Но ни человек, ни приборы не могут отличить сигнал квантованный от непрерывного. Дело в том, что как у человека, так и у приборов есть порог чувствительности Δ, из-за которого невозможно отличить два значения сигнала, если они отличаются друг от друга меньше, чем на этот порог [Л. 49]. Тем самым вводится квантование по амплитуде с уровнем q=2Δ. Ниже будет доказана теорема Котельникова о том, что непрерывный сигнал, спектр частот которого ограничен частотой f_с, можно заменить квантованным по времени сигналом с интервалом квантования

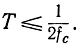
При этом не произойдет никакой потери информации.

Частотные свойства сигнала, квантованного по времени. Задачу поставим следующим образом. По заданному преобразованию Лапласа-Фурье для непрерывного сигнала X(ω) найдем это преобразование для соответствующего дискретного сигнала X*(ω) (см. рис. 5-7). Немного нарушая строгость, обозначим преобразование Лапласа-Фурье от функции x(t) через X(ω) и X(s). Аналитически дискретную функцию, представленную на рис. 5-7, б, можно записать в виде

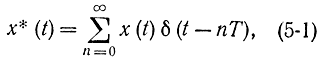
где

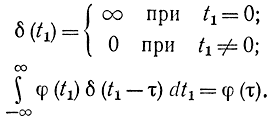
Ниже для функции X*(ω) будет дан вывод применительно к преобразованию Лапласа-Фурье, поэтому в формуле (5-1) суммирование проводится от 0 до +∞, т. е. считается, что функция равна нулю для отрицательных значений времени. Однако полученные ниже формулы остаются в силе для произвольных функций времени, в чем можно убедиться с помощью других методов [Л. 46]. Если ввести в рассмотрение функцию

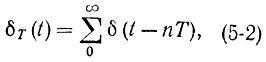
то отношение (5-1) перепишется как

Чтобы определить преобразование Лапласа - Фурье для функции х*(t) в соответствии с этим соотношением, необходимо применить формулу свертки в области комплексного переменного

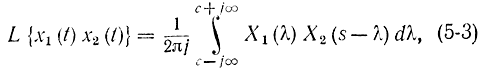
где

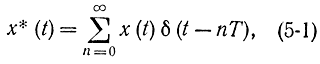
а с определяет положение прямой интегрирования, которая должна лежать правее полюсов функций Х₁ и Х₂ (рис. 5-8).

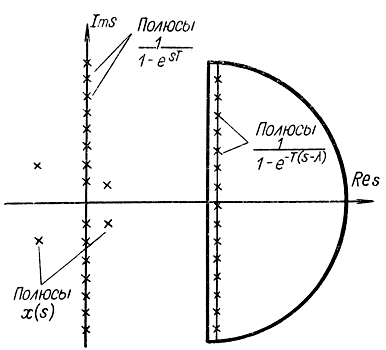
Рис. 5-8. Пояснения к выводу выражения для преобразования Лапласа дискретного по времени сигнала

Взяв от обеих частей соотношения (5-2) преобразование Лапласа - Фурье и используя формулу для бесконечной геометрической прогрессии, получим:

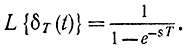
Полагая

с помощью формулы (5-3) имеем:

Интеграл в правой части будем брать с помощью вычетов. Для этого интегрирование произведем по замкнутому контуру, состоящему из прямой s=с и полуокружности большого радиуса, расположенной справа от этой прямой. Положим, что при больших значениях модуля |s| функция F(s) стремится к нулю; для этого достаточно, чтобы степень числителя была меньше степени знаменателя. Значение интеграла будет равно сумме вычетов в полюсах подынтегрального выражения, расположенных внутри замкнутого контура интегрирования. Так как полюсы функции F(λ) расположены левее прямой λ=c, то учитывать следует только полюсы выражения 1/(1-e^-T(s-λ)).Они расположены на прямой, параллельной оси ординат и находящейся на расстоянии от прямой λ=c, определяемом действительной частью величины s (рис. 5-8). В результате можем написать:

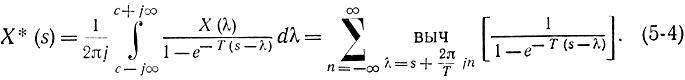
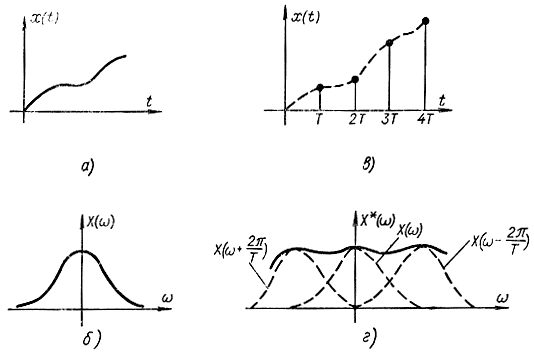
Рис. 5-9. Спектры непрерывного (а и б) и дискретного (е и г) по времени сигналов

В соответствии с правилами теории вычетов

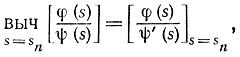
где s_n - нуль функции ψ(s), поэтому

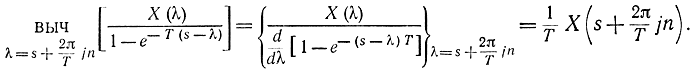
Подставив это выражение в формулу (5-4), запишем:

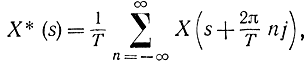
и, перейдя к соответствующим преобразованиям Фурье, получим:

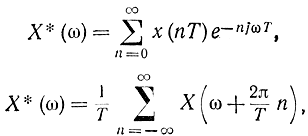
где

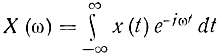
- преобразование Фурье для функции x(t).

Таким образом, спектр (преобразование Фурье) для дискретного сигнала получается из спектра непрерывного сигнала суммированием его смещенных спектров X[ω+ (2π/T)n] (рис. 5-9).

В зависимости от интервала дискретности Т для ограниченного по частоте спектра непрерывного сигнала (рис. 5-10, а) смещенные спектры могут не перекрываться (рис. 5-10,6), примыкать вплотную друг к другу (рис. 5-10,в), перекрываться (рис. 5-10,г).

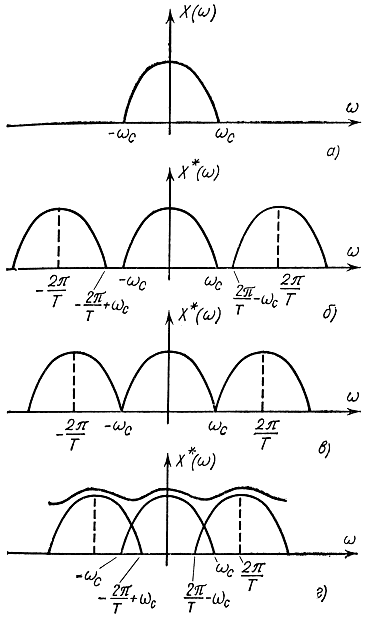
Рис. 5-10. К доказательству теоремы Котельникова

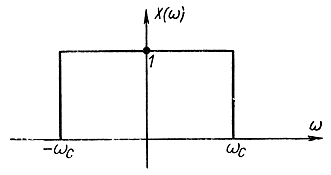
Рис. 5-11. Частотная характеристика идеального фильтра

Напомним, что речь идет о замене непрерывного сигнала дискретным (о передаче непрерывного сообщения его дискретными значениями). Очевидно, что восстановить спектр непрерывного сигнала из спектра соответствующего дискретного сигнала можно только в случаях, показанных на рис. 5-10, б, в. Сделать это в принципе можно с помощью идеального фильтра с прямоугольной частотной характеристикой (рис. 5-11), которую реально получить невозможно. В случае, показанном на рис. 5-10, г, в результате перекрытия спектров информация о непрерывном сигнале безвозмездно потеряна и ее невозможно восстановить даже с помощью идеального фильтра с частотной характеристикой. Поэтому максимально допустимое значение интервала дискретности определяется случаем, показанным на рис. 5-10, в, и равно:

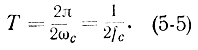
Следовательно, допустимые интервалы дискретности определяются соотношением

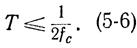
В этом и состоит теорема Котельникова. Часто в теории связи ее формулируют для случая сообщения, передаваемого в течение конечного интервала времени /0. Тогда в соответствии с формулами (5-5) и (5-6) непрерывное сообщение со спектром, ограниченным частотой, можно передать конечным числом дискретных значений, которое определяется по формуле

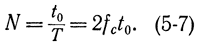
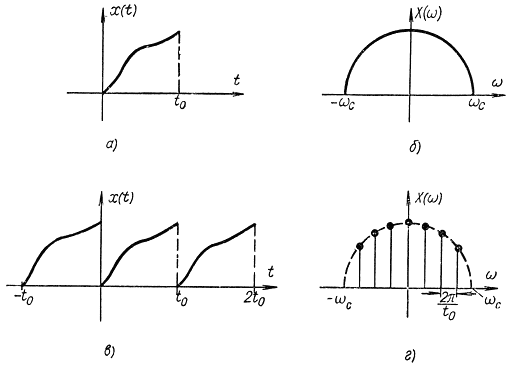
Рис. 5-12. Пояснения к теореме Котельникова для дискретного по частоте сигнала

Очевидно, что передавать непрерывное сообщение большим числом дискретных значений (т. е. с меньшим интервалом дискретности) не имеет смысла, так как при этом перегружается канал связи, а выигрыша в точности не получается.

Следует заметить, что приведенная выше формулировка теоремы Котельникова [формула (5-7)] не является строгой, так как не существует сигналов, ограниченных по времени и частоте: если сигнал обладает ограниченным спектром, то он простирается до бесконечности во времени, и, наоборот, если сигнал ограничен во времени, то он обладает бесконечным спектром.

В инженерных руководствах часто приводится частотный аналог теоремы Котельникова, который был известен значительно раньше работ Котельникова и заключается в следующем. Допустим, что имеется сигнал х(t), ограниченный во времени (рис. 5-12, а), т. е. вне интервала времени (0, t₀) сигнал равен нулю. Из теории преобразования

Фурье известно, что такую функцию можно разложить в ряд Фурье

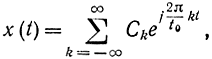
где коэффициенты ряда

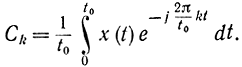
Эти коэффициенты представляют значения спектра функции (с точностью до постоянного коэффициента)

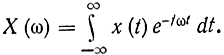
Отсюда

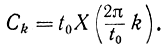
Поэтому временной сигнал, ограниченный по длительности величиной t₀, можно передавать не непрерывным спектром по частоте (рис. 5-12, б), а совокупностью дискретных значений, отстоящих на величину 2π/t₀ (и меньше этого значения) (рис. 5-12, г). Такому дискретному спектру будет соответствовать периодическая во времени функция с периодом t₀ (рис. 5-12, в). Если сигнал можно ограничить по частоте величиной ω_c=2πf_c, то для передачи без искажений такого сообщения необходимо передать конечное число дискретных значений спектра (амплитуд гармоник), равное

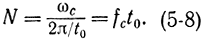
Полное совпадение с формулой (5-7) получится, если сигнал будет рассматриваться на временном интервале (-t₀, t₀), а не (0, t₀). В этом случае формула (5-8) перепишется в виде

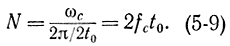
Таким образом, непрерывный сигнал, ограниченный интервалами по времени (-t₀, t₀) и по частоте (-ω_c, ω_c), можно передавать конечным числом дискретных значений функции времени или спектра, которые отстоят друг от друга на величины

соответственно. Общее число дискретных значений определяется формулой (5-9).