5-4. Передача сообщения квантами информации

Допустим, задано какое-то сообщение или сигнал, ограниченный полосой f_c и длительностью t₀ (рис. 5-17). Требуется передать его тем или иным способом. Ниже будет изложен метод Габора, который иногда называется методом информационных ячеек или фильтром Габора.

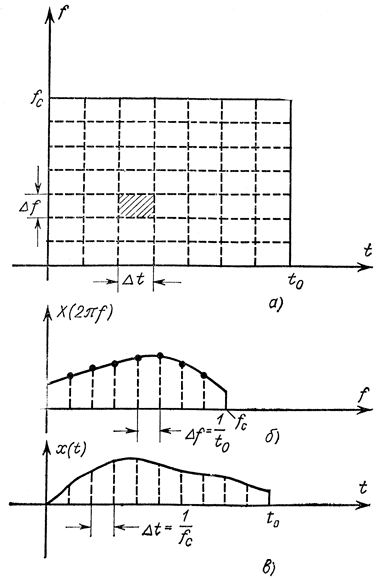
Рис. 5-17. Пояснения к передаче сигнала квантами информации

Разделим прямоугольник (f_c, t₀) на (f, t)-плоскости элементарными ячейками единичной площади ΔfΔt (рис. 5-17,а). Значения Δf и Δt можно выбирать различными, лишь бы их произведение равнялось единице. В частности, можно выбрать Δt=t₀, тогда Δf=1/t₀ и сигнал будет передаваться дискретными отсчетами по частоте с амплитудами гармоник сигнала, кратными Δf=1/t₀ (рис. 5-17, б). В другом крайнем случае можно принять Δf=f_c, тогда Δt=1/f_c. Двойка в знаменателе этой формулы отсутствует по сравнению с формулой Шеннона - Котельникова, так как в данном случае ширина спектра равна f_c, а в формуле Шеннона - Котельникова 2f_c. В этом случае сигнал будет передаваться дискретными значениями во времени, отстоящими друг от друга на интервал Δt=1/f_c (рис. 5-17, в). В обоих случаях непрерывное сообщение передается квантами: в первом случае передаются дискретные значения временной функции, во втором - дискретные значения по частоте. Возможен третий промежуточный случай, когда Δt≠t₀ и Δf≠f_c, но ΔfΔt=1 (рис. 5-17, а)у и сообщение передается своими значениями, дискретными как по частоте, так и по времени.

Сообщение передается квантами, каждому кванту соответствует квадрат на (t, f)-плоскости единичной площади. Естественно (как предлагает Габор), каждый квант следует передавать с помощью самого экономичного сигнала: гармонической составляющей (синусоидальной или косинусоидальной), промодулированной колоколообразным импульсом [формулы (5-15) и (5-16)]. Значения t⁰ и f₀ в этих формулах определяются положением соответствующего квадрата на (t, f)плоскости. Амплитуда импульса определяется значениями временной и частотной зависимостей сигнала, соответствующих данному квадрату-кванту сообщения.