5-3. Элементы квантовой теории информации

В теории информации известен принцип неопределенности, аналогичный тому, который имеется в квантовой механике.

Известно, что для передачи импульса (сигнала) шириной Δt требуется полоса пропускания по частоте Δf≥1/Δt.

Пример 5-1. При полосе Δf≈6 для передачи телевизионных сигналов при 525 строках, 30 кадрах в секунду и 360 импульсах на строку при условии неискаженной передачи допускается примерно следующий минимальный период повторения (или ширина) импульсов

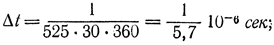
при этом

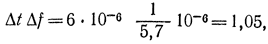
т. е. ΔfΔt≥1.

Таким образом, произведение ft имеет нижний предел для передачи сообщений без искажения.

Покажем это еще несколько другим способом [Л. 50]. Введем некоторые эффективные значения длительности и полосы сигнала x(t):

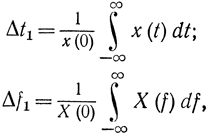
где

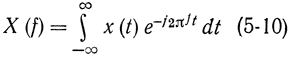
есть преобразование Фурье для сигнала;

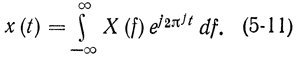
Но в соответствии с формулами (5-10) и (5-11)

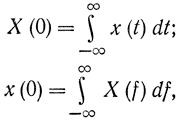
поэтому

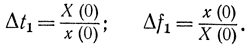
Отсюда

Физический смысл введения эффективных полос и времени сигнала заключается в замене реального сигнала эквивалентным, имеющим прямоугольную форму кривой, зависящую от времени и частоты (рис. 5-13). Ординаты этих прямоугольных кривых соответственно равны х(0) и X(0), а максимальные значения абсцисс Δt₁ и Δf₁ Площади, ограниченные кривыми реальных сигналов и их эквивалентов, равны, причем площадь берется со своим знаком: если кривая расположена над осью абсцисс, площадь положительная, если под осью абсцисс, площадь отрицательная. Очевидно, что отрицательные значения кривой сигнала, например, в зависимости от времени могут достигать больших значений и оказывать существенное влияние на характер сигнала, а эффективная длительность сигнала будет тем меньше, чем кривой сигнала, например, в зависимости от времени могут достигать больших значений и оказывать существенное влияние на характер сигнала, а эффективная длительность сигнала будет тем меньше, чем больше эти отрицательные значения и чем больше их длительность. Рассуждения относительно эффективной полосы пропускания по частоте аналогичны. Поэтому более разумно вводить эффективные значения длительности и полосы сигнала, используя абсолютные значения сигнала в зависимости от времени и частоты (рис. 5-14):

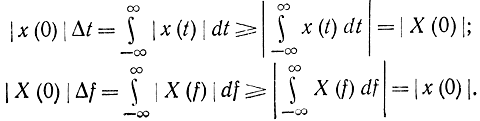
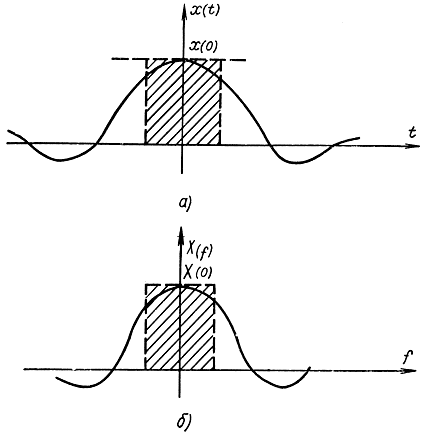
Рис. 5-13. Пояснения к введению эквивалентных по времени (а) и частоте (б) сигналов (первый вариант)

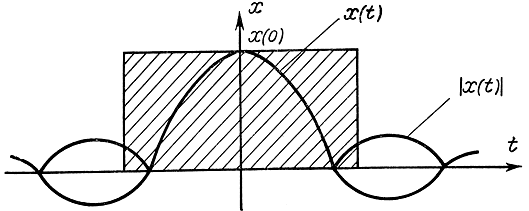
Рис. 5-14. Пояснения к введению эквивалентного по частоте сигнала (второй вариант)

Согласно этим определениям

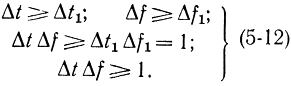
В этих соотношениях и состоит принцип неопределенности теории информации. В квантовой механике принцип неопределенности Гейзенберга заключается в том, что переменная (координата) q и ее сопряженный импульс Р не могут быть измерены одновременное любой заранее заданной высокой точностью. Если обозначить ошибки измерения этих величин соответственно через Δq и ΔP, то

В физике а равна постоянной Планка h=6,6252*10 дж*сек или ћ =h/2π (в зависимости от размерности q и Р).

В теоретической и квантовой механике энергия Е является сопряженным импульсом переменной времени t и

Далее, энергия колебания частоты f равна Е=hf. Отсюда

С помощью этого соотношения и учитывая (5-14), получаем:

Отсюда снова получаем соотношение (5-12), определяющее принцип неопределенности в теории информации.

В связи с изложенным встает вопрос об оптимальном сигнале. Какая форма зависимости сигнала от времени и частоты является наилучшей? Из свойства преобразования Фурье следует, что чем короче сигнал во времени, тем более широкой полосой частот он обладает. И наоборот, чем уже полоса частот сигнала, тем большую протяженность он имеет во времени. Аналитически эти свойства могут быть записаны в виде

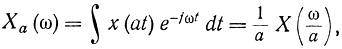
откуда следует, что с увеличением масштаба времени в а раз масштаб по частоте уменьшается в а раз. Множитель 1/а в правой части формулы принципиальной роли не играет и связан с уменьшением энергии сигнала. Это свойство сигналов отражает принцип неопределенности. Если пытаются сэкономить на времени передачи сигнала, то проигрывают в полосе частот, и наоборот. Известно, что при радиоприеме на коротких волнах для лучшей избирательности делают очень узкие резонансные контуры. Однако при этом приходится очень долго ждать, пока сигнал нарастет до нужной амплитуды (медленно вращать ручку настройки).

Аналогичные ситуации часто возникают в радиолокации. В настоящее время радиолокационные станции не строятся без систем защиты от помех. Для определения дальности до цели измеряют задержку отраженного импульса относительно излученного. В целях помехозащиты требуется еще замерять скорость движения цели на радиолокационную станцию, которая измеряется по изменению частоты принятого сигнала относительно излученного, т. е. по частоте Допплера. Для определения дальности до цели, по существу, требуется измерять фазу (задержку), а при помехозащите - скорость изменения фазы, т. е. частоту. В силу принципа неопределенности нельзя одновременно точно измерить время задержки (дальность до цели) и изменение частоты (скорость движения цели), так как увеличение точности измерения одной величины ухудшает точность измерения другой [Л. 47].

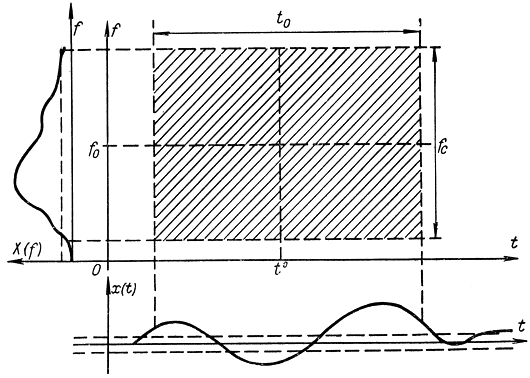
Рис. 5-15. Пояснения к оптимальному по площади сигналу

Из рассмотренного следует, что критерием оптимальности формы сигнала может служить минимум площади, занимаемой этим сигналом на плоскости время - частота (t, f) (рис. 5-15). Показано [Л. 47], что наилучшей формой сигнала в этом смысле являются синусоидальные колебания, промодулированные по амплитуде гауссовой или колоколообразной кривой (рис. 5-16). Такой сигнал может быть аналитически записан в виде

Оказывается, что эта форма записи инвариантна по отношению к преобразованию Фурье, т. е. преобразование Фурье для сигнала (5-15) имеет тот же вид:

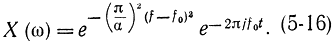
Реальный сигнал может иметь синусоидальное или косинусоидальное заполнение колоколообразного импульса (рис. 5-16).

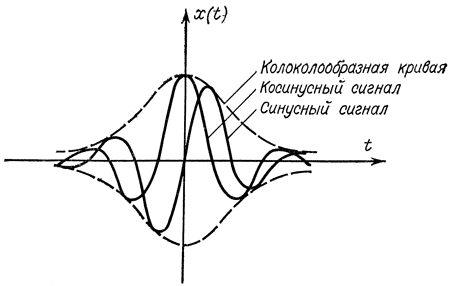
Рис. 5-16. Оптимальное по площади сигналы

Как уже отмечалось, практически ограничение сигнала по длительности t₀ и полосе частот f_c носит условный характер. Малыми значениями сигнала часто можно пренебречь, так как составляющие, например, на больших частотах не представляют интереса (не будут пропущены фильтром). Практически сигнал можно наблюдать только в течение конечного интервала времени. Поэтому сигнал при значениях времени, больших некоторого t₀, можно считать равным нулю.