а) Понятие энтропии при наличии связей между элементами

Предположим теперь, что помимо неравновероятности появления элементов в сообщении имеется вероятностная связь между их появлениями (например, вероятность появления мягкого знака после гласной буквы равна нулю). Считаем, как и раньше, что число символов в алфавите m, заданы вероятность р_i появления в сообщении i-го символа, а также условная вероятность р (j|i) появления j-го символа после i-го. Допустим, что символ j задан, т. е. известно, что с вероятностью, равной единице, этот символ присутствует в сообщении. Тогда согласно ранее выведенному выражению энтропия такого ансамбля сообщений

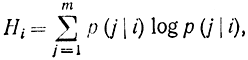
ибо при заданном i-м символе вероятность появления символа j в сообщении будет р (j|i). Но на самом деле символ i появляется в сообщении с вероятностью p_i. Величину H_i,- можно рассматривать как случайную, зависящую от номера i. Так как элемент i появляется в сообщении случайно, то и эта величина тоже будет случайной. Вероятность появления ее также равна p_i. За энтропию сообщения принимают среднее математическое ожидание величины H_i. По определению имеем:

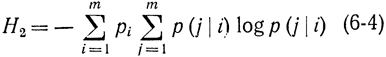
или

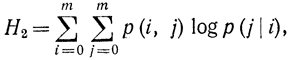
так как вероятность одновременного появления символов i и j

Если элементы сообщения равновероятны p_i1/m, то энтропия таких сообщений

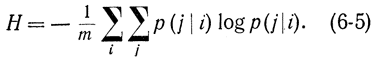
Нетрудно видеть, что при взаимосвязи символов энтропия меньше, чем без нее. Действительно, положив в предыдущей формуле p_ij=p_i получим:

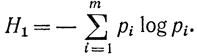
Можно распространить формулы (6-4) и (6-5) на случай, когда имеется связь не только между парами символов, а между n символами, где n>2. Тогда для описания ансамбля сообщений используется математическая модель сложно марковской, а не простейшей марковской последовательности.

С помощью рассмотренной процедуры были подсчитаны энтропии сообщений в русском и английском языках с учетом различной степени статистической связи между буквами. Предлагаем результаты этого расчета:

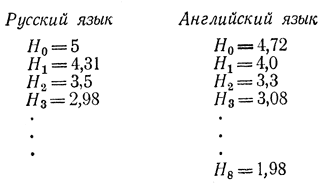
Для русского языка считалось m=32, е=ё, ь=ъ и один символ занимался под промежуток (интервал) между словами. Для английского языка подсчет был такой же, только m=27, причем считалось, что имеется 26 букв и один промежуток. Основание логарифмов равнялось двум, H₀ соответствовало случаю равновероятных и независимых друг от друга символов, Н₁ - случаю разновероятных независимых символов и т. д.

Пример 6-3. Пусть имеется всего два элемента а и b, так что m=2.

Рассмотрим случай первый, когда элементы зависимы друг от друга и не равновероятны. Вероятности их появления найдутся как

используя формулу (6-4), получаем:

Рассмотрим второй случай, когда элементы независимы, но не равновероятны:

Наконец, для случая, когда все символы равновероятны и независимы,

Как и следовало ожидать, максимальное значение энтропии получается в последнем случае, минимальное - в первом.